读《统计自然语言处理》——预备知识☞概率论和信息论基础_两个相同的正态分布其互信息值应为多少-CSDN博客

本文链接：https://blog.csdn.net/xiaopihaierletian/article/details/68925175

对于从事统计自然语言处理来说，了解概率论、信息论以及语言学知识都是很有必要的。
一、下面内容主要介绍了在统计自然语言处理中需要了解的概率论基础。

概率

如果P(A)作为事件A的概率，Ω是试验的样本空间，则概率函数满足下面三条公理：

非负性 P(A) >= 0
规范性 P(Ω) = 1
可列可加性：对于不相交的集合Aj ∈F

条件概率和独立性

假设事件B的概率已知，那么事件A发生的条件概率为（P(B) > 0）:
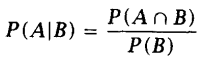
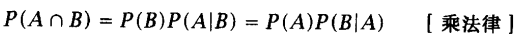
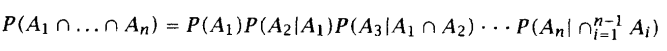
这里写图片描述

在统计自然语言处理中，上面那个链式法则很有用处，比如推导马尔可夫模型的性质。

贝叶斯定理

由条件概率和链式规则推得：
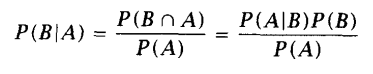
这里写图片描述
右边的分母P(A)可以看作是归一化常数，以保证其满足概率函数的性质。
如果我们感兴趣的仅仅是事件发生的相对可能性，这时可以忽略分母：

随机变量

设X为一离散型随机变量，其全部可能的值为{a1,a2,···}。那么：
pi = P(X = ai), i = 1, 2, ····
称为X的概率函数。
P(X <= x) = F(x), x∈R
称为X的分布函数。
这里写图片描述

期望和方差

这里写图片描述

联合分布和条件分布

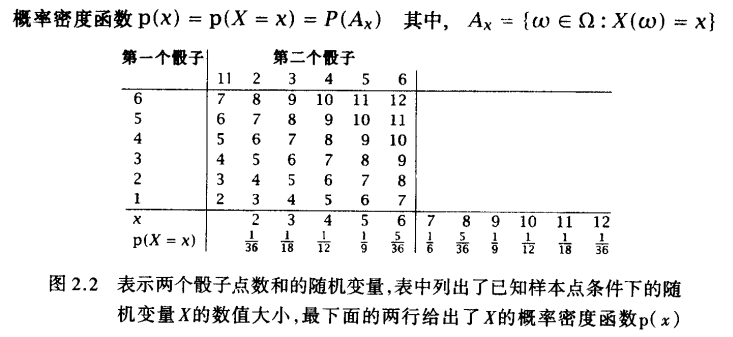
设两个离散随机变量X和Y，它们的联合密度函数可以写为：
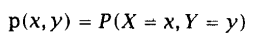
这里写图片描述
描述其中单个随机变量的概率密度函数称为边缘密度函数：

标准分布

离散分布函数：二项分布

重复一个只有两种输出的实验，并且每次实验之间相互独立时，我们认为实验结果服从二项分布（例如抛硬币实验）。
在自然语言处理中，语料库中的句子间肯定不是完全相互独立的。但是为了简化问题的复杂性，我们通常可能会做独立性假设，假设一个句子的出现独立于它前面的其他句子，近似认为它们服从二项分布。这里写图片描述
当实验有两个以上结果时，二项分布问题就转化为多项式分布（multi-nomial distribution）。

连续分布函数：正态分布

这里写图片描述

1、概率论基本概念-概率；

2、概率论基本概念-最大似然估计；

3、概率论基本概念-条件概率（概率的乘法规则）

4、概率论基本概念-贝叶斯法则（全概率公式）

例题：

一个多义词某一义项被使用的概率为1/100 000。

现有一程序判断该词在某个句子中是否使用了该义项。

如果句子中使用了该义项，程序判为“使用”的概率为0.95。

如果句子中没使用该义项，程序判为“使用”的概率为0.005。

问：该程序判断句子使用该词的这一义项的结论是正确的概率是多大？

设G：句子中使用该词的这一义项，T：程序判断句子使用该词的这一义项

P(G) = 1/100 0000 = 0.000 01

P(G’) = 1-P(G) = 0.999 99

P(T|G) = 0.95

P(T|G’) = 0.005

于是可得：

P(G|T) = [P(T|G)P(G)]/[P(T|G)P(G)+P(T|G’)P(G’)]≈0.002

5、概率论基本概念-随机变量

6、概率论基本概念-二项式分布B(n,p)

在NLP中，一般以句子为处理单位，为了简化问题的复杂性，通常假设一个句子的出现独立于它前面的其他语句，句子的概率分布近似地被认为符合二项式分布。

7、概率论基本概念-联合概率分布和条件概率分布【看课本去】

8、概率论基本概念-贝叶斯决策理论（统计方法处理模式分类问题的基本理论之一）

先验概率、后验概率

9、概率论基本概念-期望和方差

期望值指随机变量所取值的概率平均。

例题：

某个网页主菜单上有6个关键词，每个关键词被点击的概率一样，过一段时间后，这6个关键词分别被点击1，2，…，6次。

那么，平均每个关键词被点击次数的期望值就是：

E(N) = SUM(t)*p(w) = (1+2+3…+6)*1/6 = 7/2

其中t为关键词被点击次数，p为关键词被点击概率；

一个随机变量的方差描述的是该随机变量的值偏离其期望值的程度。如果X为一随机变量，那么，其方差var(X)为：

var(X) = E((X-E(X))²) = E(X²) – E²(X)

X的标准差就是sqrt(var(X))

二、信息论基础

信息是个相当宽泛的概念，很难用一个简单的定义将其完全准确的把握。然而，对于任何一个概率分布，可以定义一个称为熵(entropy)的量，它具有许多特性符合度量信息的直观要求。这个概念可以推广到互信息(mutual information)，互信息是一种测度，用来度量一个随机变量包含另一个随机变量的信息量。熵恰好变成一个随机变量的自信息。相对熵(relative entropy)是个更广泛的量，它是刻画两个概率分布之间距离的一种度量，而互信息又是它的特殊情形。

信息熵

——随机变量不确定度的度量

设p(x)为随机离散变量X的概率密度函数，x属于某个符号或者字符的离散集合 X：
p(x) = P(X = x), x ∈ X
熵表示单个随机变量的不确定性的均值，随机变量的熵越大，它的不确定性越大，也就是说，能正确估计其值的概率越小。熵的计算公式：
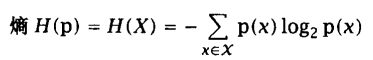
这里写图片描述
将负号移入对数公式内部：

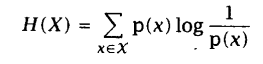
上式实际上表达的是一个加权求值的概念，权重就是随机变量X的每个取值的概率。

用E表示数学期望。如果X~p(x)，则随机变量g(X)的期望值可表示为：
这里写图片描述

当这里写图片描述：

这里写图片描述
注：X的熵又解释为随机变量的期望值，其中p(x)是X的概率密度函数。

熵的属性

H(X) >= 0;
H(X) = 0, 当且仅当随机变量X的值是确定的，没有任何信息量可言；
熵值随着信息长度的增加而增加。

例子：世界杯足球赛冠军、中文书的信息量和冗余度。

信息的作用

信息的作用在于消除不确定性，自然语言处理的大量问题就是寻找相关信息。

不确定性U，信息I，新的不确定性: U’= U - I

如果没有信息，任何公式或者数字的游戏都无法排除不确定性。合理利用信息，而非玩弄什么公式和机器学习算法，是做好搜索的关键。

例子：网页搜索

联合熵和条件熵

如果(X,Y)是一对离散随机变量，其联合概率分布密度函数为p(x,y)，(X,Y)的联合熵H(X,Y)定义为：这里写图片描述

已知随机变量X的情况下随机变量Y的条件熵：
这里写图片描述
上式实际上表示的是在已知X的情况下，传输Y额外所需的平均信息量。

例子：自然语言的统计模型，一元模型就是通过某个词本身的概率分布，来消除不确定因素；而二元及更高阶的语言模型还是用了上下文的信息，那就能准确预测一个句子中当前的词汇了。

熵的链式法则：
这里写图片描述

互信息

根据熵的链式法则，我们有如下的计算公式：
H(X,Y) = H(X) + H(Y|X) = H(Y) + H(X|Y)
所以有：
H(X) - H(X|Y) = H(Y) - H(Y|X)
这个差值称为随机变量X和Y之间的互信息（mutual information）,用I(X;Y)表示。
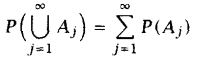
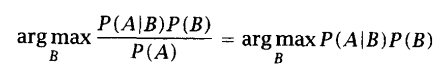
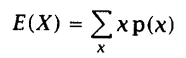
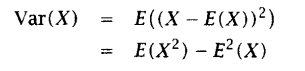
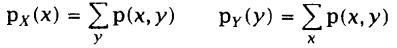
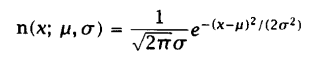
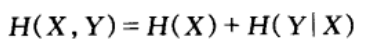
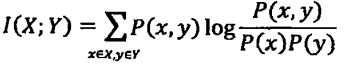
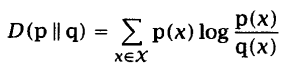
这里写图片描述