1. 定义
大O符号(Big O notation)是用于描述函数渐近行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。
2. 说明
f(n) = 2n^2 + 3n + 1
f(n) = O(n^2)
or
f(n) ∈ O(n^2)
为什么可以这么去描述?
lim( f(n) / n^2) = a ( n--> 0, a为常数)
n^2 是f(n)的最高阶,f(n)的特性由最高阶决定。
为什么不是O(2*n^2)?
O(g(n)):lim( f(n) / g(n)) = a ( n--> 0, a为常数)
当n趋近于无穷大时,f(n) / g(n)为一个常数,那么O(g(n))表示f(n)的数量级。
注:关于O(n)更加具体的数学描述请参见:
3. 常用的数量级
| 符号 | 名称 |
|---|---|
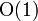 | 常数(阶,下同) |
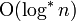 | 迭代对数 |
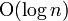 | 对数 |
![\Omicron[(\log n)^c]\!](http://upload.wikimedia.org/math/a/1/2/a1290e02605a773cc41b2583baa2c678.png) | 多对数 |
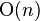 | 线性,次线性 |
 | 线性对数,或对数线性、拟线性、超线性 |
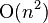 | 平方 |
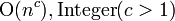 | 多项式,有时叫作“代数”(阶) |
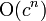 | 指数,有时叫作“几何”(阶) |
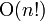 | 阶乘,有时叫做“组合”(阶) |
4. 算法的上限、下限
| 符号 | 定义 |
|---|---|
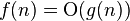 | 渐近上限 |
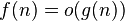 | asymptotically negligible (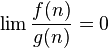 ) ) |
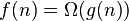 | 渐近下限 (当且仅当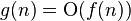 ) ) |
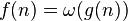 | asymptotically dominant (当且仅当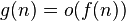 ) ) |
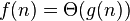 | asymptotically tight bound (当且仅当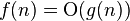 且 且 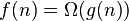 ) ) |

























 9080
9080

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








