Hard problem
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 843 Accepted Submission(s): 527
Problem Description
cjj is fun with math problem. One day he found a Olympic Mathematics problem for primary school students. It is too difficult for cjj. Can you solve it?
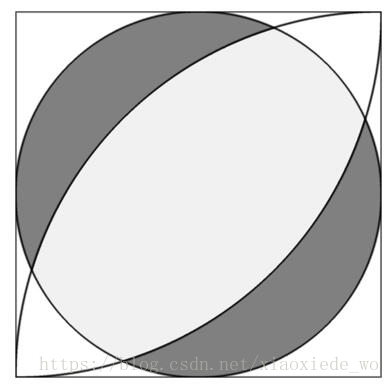
Give you the side length of the square L, you need to calculate the shaded area in the picture.
The full circle is the inscribed circle of the square, and the center of two quarter circle is the vertex of square, and its radius is the length of the square.
Input
For each test case, print one line, the shade area in the picture. The answer is round to two digit.
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 843 Accepted Submission(s): 527
Problem Description
cjj is fun with math problem. One day he found a Olympic Mathematics problem for primary school students. It is too difficult for cjj. Can you solve it?

Give you the side length of the square L, you need to calculate the shaded area in the picture.
The full circle is the inscribed circle of the square, and the center of two quarter circle is the vertex of square, and its radius is the length of the square.
Input
The first line contains a integer T(1<=T<=10000), means the number of the test case. Each case contains one line with integer l(1<=l<=10000).
For each test case, print one line, the shade area in the picture. The answer is round to two digit.
Sample Input
1 1
Sample Output
0.29
(area_S表示S的面积)
以正方形左下角为坐标轴原点,分别以正方形下边、左边为X轴,Y轴,以左上角为圆心(0,l)半径为l作圆S1,以右下角(l,0)为圆心半径为l作圆S2,正方形内切圆是以(l/2,l/2)为圆心,l/2为半径的圆S。
思路:求出圆S与圆S1相交部分面积area1和圆S与圆S2的相交面积area2,设S中空白部分面积为X,有area1+area2-X=area_S;求出X,用area_S-X即得阴影部分面积。area1与area2是相等的,所以用求出一个即可。
只要敲出两圆相交面积模板就行了:
#include<stdio.h>
#include<iostream>
#include<cmath>
using namespace std;
#define pi acos(-1.0)
typedef struct node
{
double x;
double y;
}point;
//两圆相交求阴影面积
double AREA(point a, double r1, point b, double r2)
{
double d = sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
if (d >= r1+r2)
return 0;
if (r1>r2)
{
double tmp = r1;
r1 = r2;
r2 = tmp;
}
if(r2 - r1 >= d)
return pi*r1*r1;
double ang1=acos((r1*r1+d*d-r2*r2)/(2*r1*d));
double ang2=acos((r2*r2+d*d-r1*r1)/(2*r2*d));
return ang1*r1*r1 + ang2*r2*r2 - r1*d*sin(ang1);
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
point a, b;
a.x=n*1.0/2, a.y=n*1.0/2;
b.x=n*1.0, b.y=0.0;
double result = AREA(a, n*1.0/2.0, b, n*1.0);
printf("%.2lf\n",2.0*pi*(n*1.0/2.0)*(n*1.0/2.0)-2.0*result);
}
return 0;
}









 这是一个关于解决数学问题的博客,涉及计算两个特定圆在正方形内相交部分的面积。题目给出T个测试用例,每个用例包含正方形边长l。通过求解两圆相交的面积area1和area2,并减去正方形内切圆的面积area_S,可以得到阴影部分的面积。由于area1和area2相等,因此只需计算其中一个。博客主要聚焦于两圆相交面积的计算模板。
这是一个关于解决数学问题的博客,涉及计算两个特定圆在正方形内相交部分的面积。题目给出T个测试用例,每个用例包含正方形边长l。通过求解两圆相交的面积area1和area2,并减去正方形内切圆的面积area_S,可以得到阴影部分的面积。由于area1和area2相等,因此只需计算其中一个。博客主要聚焦于两圆相交面积的计算模板。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








