时间复杂性的阶的判断以及计算方法

研究的主要目的是一个算法所需要的时间和空间，即当给出合法的输入时，为了得到输出，该算法所需要的时间和空间。

时间复杂度大小排序

时间复杂度的排序是O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) <O(n^3)< O(2^n) < O(n!) < O(n^n)。

O(1):常数时间复杂度

O(log(n)):对数时间复杂度

O(n)：线性时间复杂度

O(n^2)：平方时间复杂度

O(n^3)：立方时间复杂度

O(k^n)：指数时间复杂度，k表示常数

O(n!)：阶乘时间复杂度

举例O(1)
int n=1;
​
System.out.println(n);

​

O(n)
​
for(int i=0;i<n;i++)
​
{
​
    System.out.println(i);
​
}

O(n^2)
​
for(int i=0;i<n;i++)
​
{
​
    for(int j=0;j<n;j++)
​
    {
​
        System.out.println(i+j);
​
    }
​
}

O(log(n))
//这里演示以2为底n的对数
for(int i=0;i<n;i=i*2)
{
    System.out.println(i);
}

O(2^n)
/**
*递归求斐波那契数列的第n项
*/
int fib(int n)
{
    if(n<2)
    {
        return n;
    }
    return fib(n-1)+fib(n-2);
}

时间复杂度的计算方法

时间复杂度的判断，以一段代码的最高复杂度为准；判断一段代码的时间复杂度，，就是看内部某段代码的执行次数，谁执行次数最多时间复杂度就是多少。

例题(1)

void fun（int n）
{
    int i=1;
    while(i<=n)
        i=i*2;
}

对于while循环我们设置执行次数为t

因为i=i*2

t	i
1	2
2	4
3	8

退出while循环的条件是i>n,观察图表可知，i与t存在 i=2^t

可知当2^t>n时，退出循环

log2(2^t)>log2(n)

t>log2(n)

可知时间复杂度为log2(n)

例题（2）

x=2;
while(x<n/2)
x=2*x

此题与上题不同之处在于while中的条件发生改变，但是理解时间复杂度的，1/2相对于趋于无穷大的n来说，作用相当于没有，因此，此时可以将其看成n，可知此代码时间复杂度仍然是log2(n)

例题（3）

求整数n（n>=0）的阶乘的算法如下，其时间复杂度是（）。

int fact(int n)
{
    if(n<=1) return 1;
    return n*fact(n-1);
}

在这里再次强调时间复杂度的计算结果看的是代码的执行次数

此代码是一个递归代码

当n时，，此时返回n*fact(n-1)

当n-1时，此时返回n-1*fact(n-2)

....

当n=2时，返回2*1

当n=1时，返回1

将这些中的函数替换可得

总的返回结果为：n(n-1)(n-2)....2*1

这时不要将时间复杂度误以为是n!,看执行的次数，一共是n个值相乘，执行了n次，故时间复杂度为O(n)

例题（4）

count=0;
​
for(k=1;k<=n;k*=2)
{
    for(j=1;j<=n;j++)
    {
        count++;
    }
}

外面的for循环的时间执行次数为log2(n),里面的执行次数是n,所以总的时间复杂度为n*log2(n)

例题（5）

int func(int n)
​
{
​
    int i=0,sum=0;
    while(sum<n) sum+=++i;
    return i;
​
}

执行次数为t

t	i	sum
1	1	0+1=1
2	2	0+1+2=3
3	3	0+1+2+3=6
t	t	0+1+2+...+t

可知t与sum的关系

sum=t(t+1)/2

退出循环的条件 sum>n 等价于t(t+1)/2>n

解得n=(1+8n)^(1/2)/2可得时间复杂度为O(n^(1/2))

例题（6）

void fun(int n)
{
    int i=0;
    while(i*i*i<=n)
    {
        i++;
    }
}

设执行次数为t，

根据i++可知，i与t的关系为i=t,所以只要t * t * t>n即可

t^3>n

t=n^(1/3)

例题（7）

for(i=n-1;i>1；i--)
{
    for(j=1;j<i;j++)
    {
        if(A[j]>A[j+1])
        {
            A[j]与A[j+1]对换；
        }
    }
}

其中n为正整数，则最后一行语句的频度在最坏情况下是（）

这边内嵌for循环受到外套for循环的影响，不能单独拿出来

所以要用累加计算

如下图

例题（8）

求m++的执行次数

int m=0,i,j;
for(i=1;i<=n;i++)
{
    for(j=1;j<2*i;j++)
    {
        m++;
    }
}

这题也要用累加法

如下图

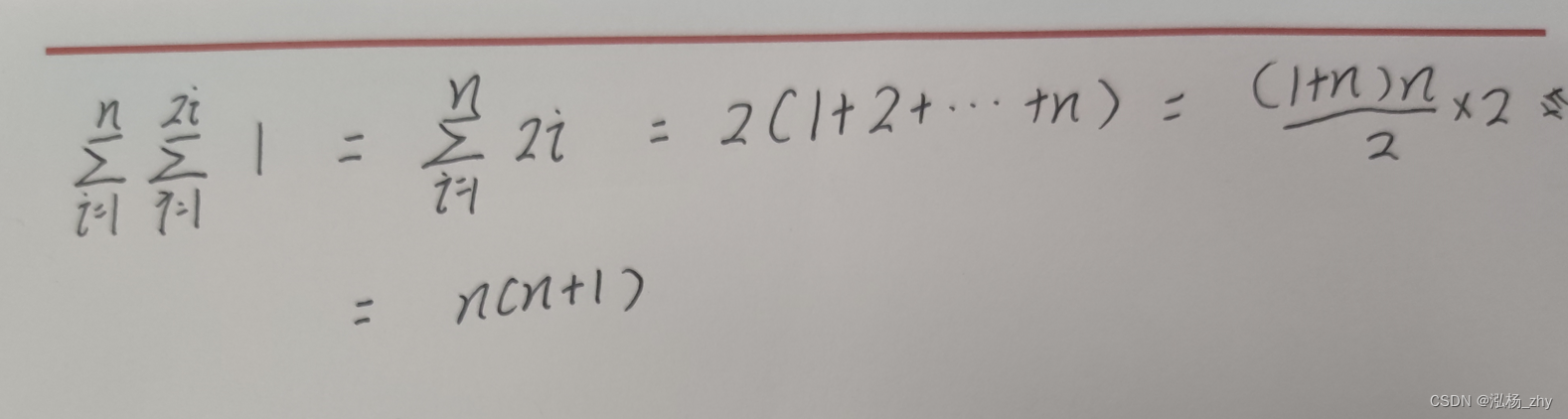
所以时间复杂度为O（n^2）

执行次数

为n*(n-1)

例题（9）

n为非负整数，程序段的时间复杂度是（）

x=0;
while(n>=(x+1)*(x+1))
x=x+1;

设执行次数为t

x与t的关系

x=t退出循环条件n<(t+1)*(t+1)

可求得时间复杂度为O（n^(1/2)）