堆排序

二叉堆的性质

二叉堆是一颗完全二叉树，最后一层的叶子从左到右排列，其它的每一层都是满的
最小堆父结点小于等于其每一个子结点的键值，最大堆则相反
每个结点的左子树或者右子树都是一个二叉堆

堆的存储

通常堆是通过一维数组来实现的。在起始数组为 0 的情形中：

父节点i的左子节点在位置 (2*i+1);
父节点i的右子节点在位置 (2*i+2);

子节点i的父节点在位置 floor((i-1)/2);

思路：

首先我们需要把树通过调整变为最小堆，则最小堆的根节点（也就是数组的第一个元素）即满足了是该序列的最小值，然后我们把它和数组的最后一个元素交换（目的就是把当前的最小值保存到数组的尾部），接下来我们对新形成的树（除去最后一个节点，因为最后一个节点已经是当前最小值了）进行调整，再次变为新的最小堆，最小堆的根节点即为当前新的最小值，再把该最小值与数组的倒数第二个数交换，则数组的倒数第二个数子即为序列的第二小的数字；现在，以此类推，直到新的树中只有一个节点为止，则此时，保存在数组中的数字满足从大到小的顺序。这就是堆排序作为选择排序的一种的排序过程。

把根节点调节到合适的节点：

void MinHeapFixdown(int *a, int i, int n)  //i表示当前节点，n表示节点数
{
	int j,temp;  //j为子节点
	temp = a[i]; //父节点放到temp
	j = i*2 + 1;  

	while (j < n)
	{
		if(j + 1 < n && a[j+1] < a[j])  //如果i的子节点有两个，选择最小那个，即为j
			j++;
		if(temp <= a[j])               //如果j比父节点要大，即退出循环
			break;
		a[i] = a[j];                  //把较小的节点与父节点交换，即上移
		i = j; 
		j = 2*i+1;
	}

	a[i] = temp;
}

建立一个小顶堆，从第一个非叶子节点开始：

void MakeMinHeap(int *a, int n)
{
	for (int i = n/2 - 1; i >=0; i--)
	{
		MinHeapFixdown(a, i, n);
	}
}

这时进行堆排序即可：

void MinHeapSort(int *a, int n)
{
	MakeMinHeap(a, n);
	for (int i = n - 1; i > 0; i--)
	{
		swap(a[i], a[0]);
		MinHeapFixdown(a, 0, i);
	}
}

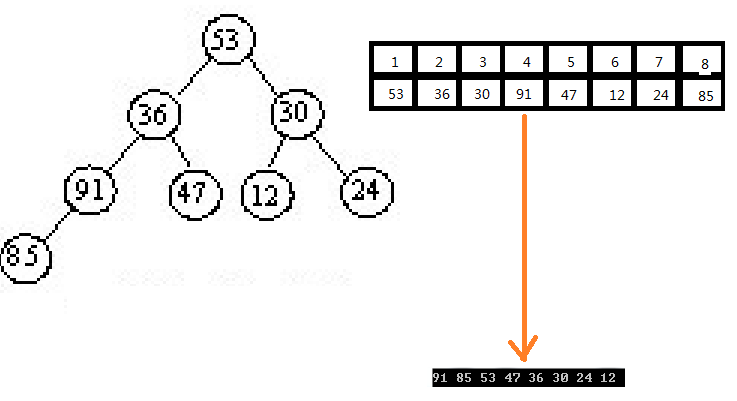
实例：

先建立小顶堆，得到如图所示：

在得到是有序最大堆

代码如下：

// chahch.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>

using namespace std;

void MinHeapFixdown(int *a, int i, int n)  //i表示当前节点，n表示节点数
{
	int j,temp;  //j为子节点
	temp = a[i]; //父节点放到temp
	j = i*2 + 1;  

	while (j < n)
	{
		if(j + 1 < n && a[j+1] < a[j])  //如果i的子节点有两个，选择最小那个，即为j
			j++;
		if(temp <= a[j])               //如果j比父节点要大，即退出循环
			break;
		a[i] = a[j];                  //把较小的节点与父节点交换，即上移
		i = j; 
		j = 2*i+1;
	}

	a[i] = temp;
}

void MakeMinHeap(int *a, int n)
{
	for (int i = n/2 - 1; i >=0; i--)
	{
		MinHeapFixdown(a, i, n);
	}
}

void MinHeapSort(int *a, int n)
{
	MakeMinHeap(a, n);
	for (int i = n - 1; i > 0; i--)
	{
		swap(a[i], a[0]);
		MinHeapFixdown(a, 0, i);
	}
}

int _tmain(int argc, _TCHAR* argv[])
{
	int arr[] = {53,36,30,91,47,12,24,85};
	MinHeapSort(arr, 8);

	for (int i = 0; i < 8; i++)
	{
		cout << arr[i] << " ";
	}
	
	return 0;
}

-------------------------------------------------------

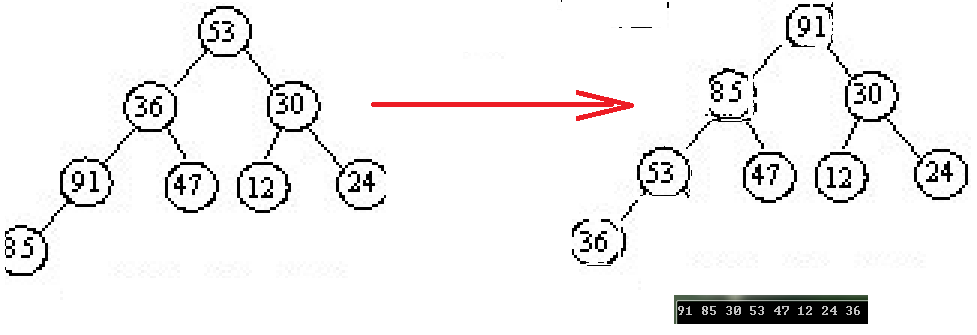
如果建立有序最小堆呢

即将上述上述建立的小顶堆修改为大顶堆即可：

//建立大顶堆
void MaxHeapFixdown(int *a, int i, int n)  //i表示当前节点，n表示节点数  
{
	int j,temp;  //j为子节点
	temp = a[i]; //父节点放到temp
	j = i*2 + 1;  

	while (j < n)
	{
		if(j + 1 < n && a[j+1] > a[j])  //如果i的子节点有两个，选择最大那个，即为j
			j++;
		if(temp >= a[j])               //如果j比父节点要小，即退出循环
			break;
		a[i] = a[j];                  //把较大的节点与父节点交换，即上移
		i = j; 
		j = 2*i+1;
	}

	a[i] = temp;
}

void MakeMinHeap(int *a, int n)
{
	for (int i = n/2 - 1; i >=0; i--)
	{
		MaxHeapFixdown(a, i, n);
	}
}

如图所示：

在此基础上再排序。得到最终有序最小堆

代码如下：

// chahch.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>

using namespace std;

//建立小顶堆
void MinHeapFixdown(int *a, int i, int n)  //i表示当前节点，n表示节点数  
{
	int j,temp;  //j为子节点
	temp = a[i]; //父节点放到temp
	j = i*2 + 1;  

	while (j < n)
	{
		if(j + 1 < n && a[j+1] < a[j])  //如果i的子节点有两个，选择最小那个，即为j
			j++;
		if(temp <= a[j])               //如果j比父节点要大，即退出循环
			break;
		a[i] = a[j];                  //把较小的节点与父节点交换，即上移
		i = j; 
		j = 2*i+1;
	}

	a[i] = temp;
}

//建立大顶堆
void MaxHeapFixdown(int *a, int i, int n)  //i表示当前节点，n表示节点数  
{
	int j,temp;  //j为子节点
	temp = a[i]; //父节点放到temp
	j = i*2 + 1;  

	while (j < n)
	{
		if(j + 1 < n && a[j+1] > a[j])  //如果i的子节点有两个，选择最大那个，即为j
			j++;
		if(temp >= a[j])               //如果j比父节点要小，即退出循环
			break;
		a[i] = a[j];                  //把较大的节点与父节点交换，即上移
		i = j; 
		j = 2*i+1;
	}

	a[i] = temp;
}

void MakeMaxHeap(int *a, int n)
{
	for (int i = n/2 - 1; i >=0; i--)
	{
		MaxHeapFixdown(a, i, n);
	}
}

void MaxHeapSort(int *a, int n)
{
	MakeMaxHeap(a, n);
	for (int i = n - 1; i > 0; i--)
	{
		swap(a[i], a[0]);
		MaxHeapFixdown(a, 0, i);
	}
}

int _tmain(int argc, _TCHAR* argv[])
{
	int arr[] = {53,36,30,91,47,12,24,85};
	MaxHeapSort(arr, 8);
	

	for (int i = 0; i < 8; i++)
	{
		cout << arr[i] << " ";
	}
	
	return 0;
}