离散数学8__第3章谓词逻辑

本章在离散数学 这门课程是一个重点，考试分数在所有题目占比约13%， 很重要。

首先看知识结构图

要学习本章， 必须先了解 有关的概念。

一 谓词的概念

谓词用来指明个体的性质或个体之间的关系等， 常用大写的英文字母P, Q, R... 来表示。

表示具体性质或关系的谓词称为谓词常项， 表示抽象的或泛指的性质或关系的谓词称为谓词变项。

谓词变项的定义： 由一个谓词、一些个体变量组成的表达式称为谓词变项 或命题函数。

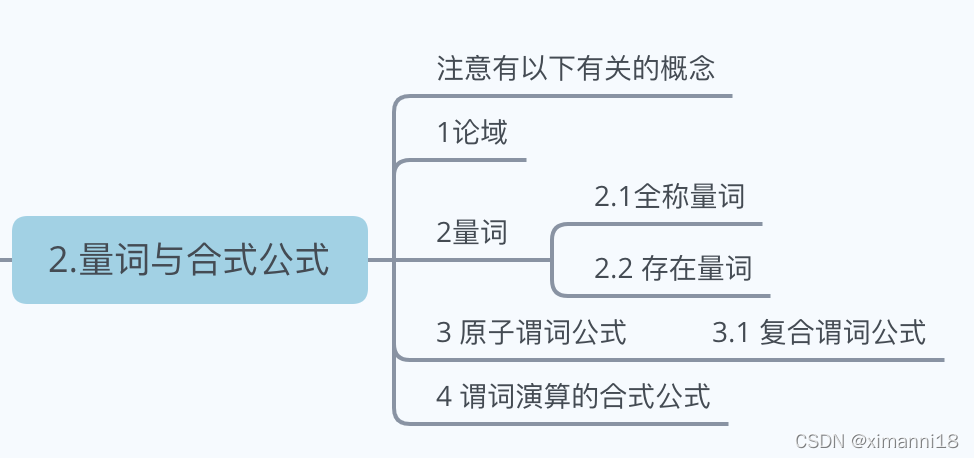
二 量词与合式公式

命题函数中表示数量的词称为量词，可以使用量词来表示个体常项与变项之间的数量关系， 即对命题函数进行量化。 量词分为两种， 一是全称量词， 二是存在量词。

在数学语句中， 经常用断定某一性质对变量在某一特定域内的所有值为真， 这一特定域即是论域。

注意一下有关概念

 

注意一个规律：

∀ᵪ 后面一定是 → 

∃ᵪ 后面一定是 ∧

~~~~~~~

∀ 读作 “任何的”

∃ 读作 “存在着”

注意： 谓词合式公式没有 ⇔、⇒ 符号

三  谓词演算的等价式与蕴涵式

在谓词公式中常包含命题变元和个体变元， 当个体变元用确定的个体取代， 命题变元用确定的命题所取代时， 就称作  对谓词公式赋值（或解释）。

 

四 前束范式

定义： 一个公式，如果量词均在全式的开头， 它们的作用域， 延伸到整个公式的末尾， 则该公式称为前束范式。

量词就是：∀， ∃

例如   是前束范式，    不是前束范式。

 五  谓词演算的推理理论

谓词演算的推理方法， 可以看做是命题演算推理方法的扩展。

本文介绍一些关于消去和添加量词的规则：

（1）全称量词消去规则（简记为 ∀ -)

  (2) 全称量词引入规则 （简记为 ∀ +）

（3）存在量词消去规则 (简记为 ∃- ）

 （4）存在量词引入规则(简记为 ∃+)

看一个例题

题： 证明前提 "在本离散数学课上的每个人学过一门计算机课程" 和 "李明是本课上的学生"  可得出结论“李明学过一门计算机课程”。

解： 设D(x): x在本离散数学课上;   C(x): x学过一门计算机课程； m: 李明。 

  则前提可表示为:   , 结论是C(m). 

构造推理证明如下:

  (1)       P规则

 (2)                 

(3) 

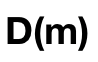
(4)                       T（2）(3)