对于绝对值函数的定积分,解法要区分对待,| |里面的值>0和 <0,分两种情况分析.
看一个例题:
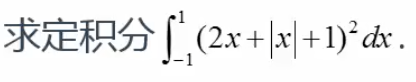
分析: 如何区分情况来分析呢? 我们知道当 x > 0 时, |x| = x; 当 x<0 时,
|x| = -x. 如何判断>0 还是<0, 根据积分区域来判断!
在本题,当 0 ≤ x < 1 时, |x| = x,
当 -1< x<0 时, |x|=-x.

再看一个例题

总结: 绝对值函数的定积分的求解, 就是划分区间,再计算各段之和。
对于绝对值函数的定积分,解法要区分对待,| |里面的值>0和 <0,分两种情况分析.
看一个例题:
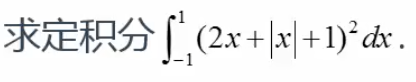
分析: 如何区分情况来分析呢? 我们知道当 x > 0 时, |x| = x; 当 x<0 时,
|x| = -x. 如何判断>0 还是<0, 根据积分区域来判断!
在本题,当 0 ≤ x < 1 时, |x| = x,
当 -1< x<0 时, |x|=-x.

再看一个例题

 1762
1762

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


