本篇博文是单变量线性回归与梯度下降的拓展,使之能在正式生产中更好地落地
http://blog.csdn.net/xinzhi8/article/details/64919106 代价函数与梯度下降算法(一)(代价函数又称成本函数)
http://blog.csdn.net/xinzhi8/article/details/64948465 代价函数与梯度下降算法(二)
在阅读这篇博文之前,除去之前博文的数学知识,你还需要了解的数学知识:
1,偏导数
2,线性代数
一,多变量梯度下降
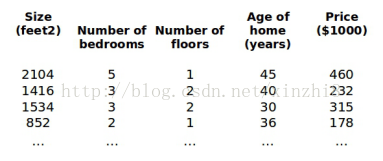
目前为止,我们探讨了单变量/特征的回归模型,现在我们对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为(x1,x2,...,xn)。
增添更多特征后,我们引入一系列新的注释:
n 代表特征的数量
x(i)代表第 i 个训练实例,是特征矩阵中的第 i 行,是一个向量(vector)。
支持多变量的假设 h 表示为:hq (x ) = q 0 + q1 x1 + q 2 x2 + ... +qn xn这个公式中有 n+1 个参数和 n 个变量,为了使得公式能够简化一些,引入 x0=1,则公式转化为:
此时模型中的参数是一个 n+1 维的向量,任何一个训练实例也都是 n+1 维的向量,特征矩阵 X 的维度是 m*(n+1)。因此公式可以简化为: hq (x ) =qT X ,其中上标 T 代表矩阵转置。与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,即:
我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。多变量线性回归的批量梯度下降算法为:

我们开始随机选择一系列的参数值,计算所有的预测结果后,再给所有的参数一个新的值,如此循环直到收敛。当你仔细阅读我之前的博文并有高等数学基础,你会发现多变量梯度下降其实很简单
二,特征缩放
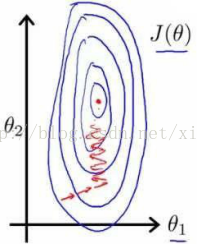
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000 平方英尺,而房间数量的值则是 0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。如图:
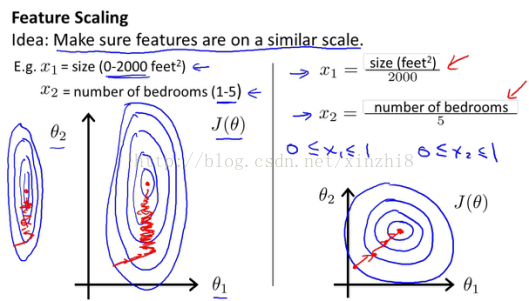
最简单的方法是令:
本博文参阅斯坦福大学吴恩达(Andrew Ng)机器学习课程,同时感谢黄海广博士的指导,转载请标明出处









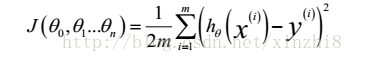
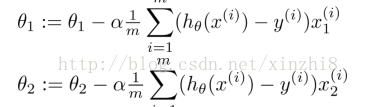


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








