matlab简单分析频域滤波和时域滤波

最新推荐文章于 2024-08-18 20:07:57 发布

只是有点小怂

最新推荐文章于 2024-08-18 20:07:57 发布

阅读量1.2w

点赞数 10

分类专栏：信号matlab

本文链接：https://blog.csdn.net/xiong_xin/article/details/105347130

版权

信号matlab 专栏收录该内容

25 篇文章

订阅专栏

本文深入探讨了信号处理中的滤波技术，包括频域滤波、时域滤波器设计、数字差分高通滤波及数据平滑低通滤波等。通过具体实例，演示了如何使用MATLAB进行信号的低通、高通滤波，以及如何设计和应用高斯平滑滤波器。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

华中科技大学《数字信号分析理论实践》第六单元信号数字滤波的概念学习总结记录

频域滤波

在这里插入图片描述

对信号进行低通滤波的一种快速方法，低频信号幅度设为1，负频率镜像过去，把虚部设为0

Fs = 2048;
dt = 1.0/Fs;
T = 1;
N = T/dt;
t = linspace(0,T,N);
x1 = sin(2*pi*50*t)+sin(2*pi*300*t)+sin(2*pi*500*t);
subplot(411);
plot(t,x1);
axis([0,0.1,-2,2]);
P = fft(x1,N);
Pyy = 2*sqrt(P.*conj(P))/N;
f = linspace(0,Fs/2,N/2);
subplot(412)
plot(f,Pyy(1:N/2));
P1(N) = 0;
for k = 1:N
	P1(k) = real(P(k))+1i*imag(P(k));
end
for k = 200:N-200
	P1(k) = 0;
end
Pyy = 2*sqrt(P1.*conj(P1))/N;
subplot(413)
plot(f,Pyy(1:N/2));
x2 = ifft(P1);
subplot(414);
plot(t,real(x2));
axis([0,0.1,-2,2]);

在这里插入图片描述

长数据滤波

数字时域滤波器——关键得到Z变换形式的滤波器

数字差分——简单的高通滤波器
$x'(n)\approx\frac{x(n+1)-x(n-1)}{2\Delta t}\Rightarrow H(z)=az^1-az^{-1},a = \frac{1}{2\Delta t}$

a = 1/(2*dt);
For K = 1 To N-1
	x(k) = a*x(k+1)-a*x(k-1)
Next

在这里插入图片描述

Fs = 5000;
dt = 1/Fs;
T = 1;
N = T/dt;
t = linspace(0,T,N);
a = 5;
f = 2;
y = a*sin(2*pi*f*t)+0.3*sin(2*pi*50*t);
subplot(211)
plot(t,y);
x(N) = 0;
for i = 2:N-1
	x(i) = (y(i+1)-y(i-1))/2;
end
subplot(212)
plot(t,x);

数据平滑——简单的低通滤波器

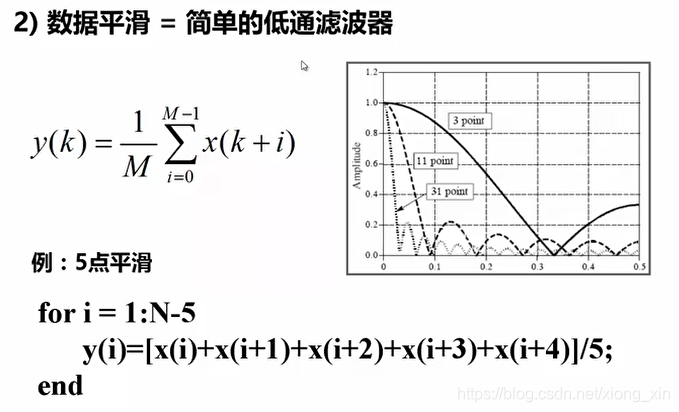
Fs = 5000;
dt = 1/Fs;
T = 1;
N = T/dt;
t = linspace(0,T,N);
a = 5;
f = 2;
y = a*sin(2*pi*f*t)+0.8*sin(2*pi*500*t);
subplot(211)
plot(t,y);
x = y;
for i = 1:N-5
	x(i) = (y(i)+y(i+1)+y(i+2)+y(i+3)+y(i+4))/5;
end
subplot(212)
plot(t,x);

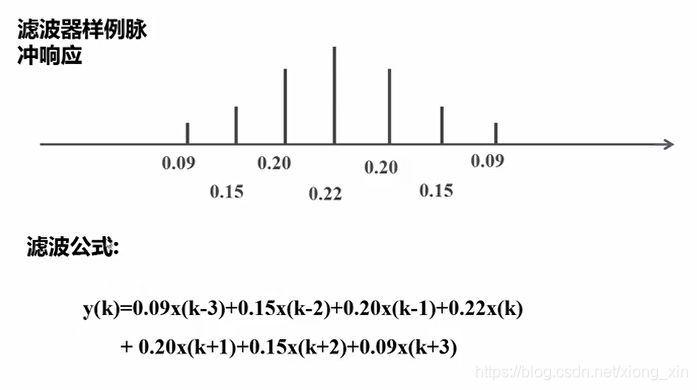
在这里插入图片描述