差分约束系统学习记录

预备知识： 最短路算法其应用

一、什么是差分约束系统

对于下面一组不等式：
x1-x2<=0
x1-x5<=1
x2-x5<=1
x3-x1<=5
x4-x1<=4
x4-x3<-1
x5-x3<=-3
x5-x4<=-3
特点是全都是两个未知数的差 小于等于(或大于等于) 某个常数(大于等于也可以，因为左右乘 −1 就可以化成小于等于的形式 ) ，这样的不等式组称作差分约束系统。
这个不等式组要么无解，要么就有无限组解。因为如果存在一组解 {x1,x2,…,xn}的话，那么对于任何一个常数 k 有 {x1+k,x2+k,…,xn+k} 也肯定是一组解，因为任何两个数加上一个数以后，它们之间的关系（差值）是不变的，这个差分约束系统中的所有不等式都不会被破坏。

二.构图求解

（这里指x[s]-x[t]的max或min）

数形结合

对一个不等式变形(等价变形)：x[i]-x[j]<=a[k] 有:x[j]+a[k]>=x[i]
将不等式中的i和j变量替换掉，i = v， j = u，将x数组的名字改成dis,令a[k] = w(j, i)：dis[u]+w(u,v)>=dis[v];
这时候联想到SPFA中的relax():

if(dis[u]+w<dis[v])
{
	dis[v]=dis[u]+w;
	q.push(v);
}

求x[n-1] - x[0] 的最大值：（最小值等下说）
对比上面两个不等式，两个不等式的不等号正好相反，但是再仔细一想，其实它们的逻辑是一致的，因为SPFA的松弛操作是在满足小于的情况下进行松弛，力求达到d[u] + w(u, v) >= d[v]，而我们之前令a[k] = w(j, i)，所以我们可以将每个不等式转化成图上的有向边：
对于每个不等式 x[i] - x[j] <= a[k]，add(j,i,a[k]); 对结点 j 和 i 建立一条 j到i的有向边 ，边权为a[k]，求x[n-1] - x[0] 的最大值就是求 0 到n-1的最短路(如图)。

三.三角不等式

我们来看下面三个不等式：
B-A<=c (1)
C-B<=a (2)
C-A<=b (3)
求C-A的最大值？
(1)+(2)得：C-A<=a+c
所以这个问题实质是求min(b,a+c).按上面的方式建图：

我们发现min{b, a+c}正好对应了A到C的最短路，而这三个不等式就是著名的三角不等式。将三个不等式推广到m个，变量推广到n个，就变成了n个点m条边的最短路问题了。

四、最大解与最小解

（这里指x[s]-x[t]的max或min）
差分约束解不等式组分为两种方法：最短路和最长路。
重要结论：

1.以 xi−xj<=y为约束条件，建图 add(j,i,y) 求最短路后得到的是最大解，所有的解都不大于且尽可能逼近 dis[x0]

2.以 xi−xj>=y为约束条件，建图 add(j,i,y) 求最长路后得到的是最小解，所有的解都不小于且尽可能逼近 dis[x0]

最短路对应最大解，最长路对应最小解，做题时根据实际情况选用；

五、解的存在性

解的情况有三种：（这里指x[s]-x[t]的max或min）

1.有解

2.无解:有负(正)环

最短路上有负环，最长路上有正环；
最短路无限短，最长路无限长；
表现为X[t] - X[s] <= T中T无限小，X[t] - X[s] >= T中T无限大；

3.无限多解:图不连通

最短路无限长，最长路无限短；
表现为X[t] - X[s] <= T中T无限大，X[t] - X[s] >= T中T无限小；

注意：实际实现时可以把最长路转化为最短路，因此只需判负环和dis[t]是否无穷大；

六、增加源点（超级源点）

具体实现时，常在原图上附加一个点，与每个点都连接一条w=0的边；
以下列不等式为例：


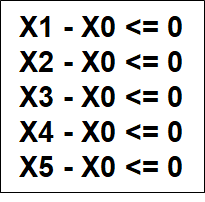
以 v0 为源点，求单源最短路，最终得到的 v0 到 vi 的最短路径长度就是 xi 的一个解；
作用：1.可以限制所有的未知数的解都不大于0 （由上面第1个重要结论可以得到）
2.判负环（图不连通时）
好像还有更多…

七、应用

1.线性约束（P4878）

线性约束一般是在一维空间中给出一些变量（一般定义位置），然后告诉你某两个变量的约束关系，求两个变量a和b的差值的最大值或最小值。
【例题1】N个人编号为1-N，并且按照编号顺序排成一条直线，任何两个人的位置不重合，然后给定一些约束条件。
X(X <= 100000)组约束Ax Bx Cx(1 <= Ax < Bx <= N)，表示Ax和Bx的距离不能大于Cx。
Y(X <= 100000)组约束Ay By Cy(1 <= Ay < By <= N)，表示Ay和By的距离不能小于Cy。
如果这样的排列存在，输出1-N这两个人的最长可能距离，如果不存在，输出-1，如果无限长输出-2。
像这类问题，N个人的位置在一条直线上呈线性排列，某两个人的位置满足某些约束条件，最后要求第一个人和最后一个人的最长可能距离，这种是最直白的差分约束问题，因为可以用距离作为变量列出不等式组，然后再转化成图求最短路。
令第x个人的位置为d[x]（不妨设d[x]为x的递增函数，即随着x的增大，d[x]的位置朝着x正方向延伸）。
那么我们可以列出一些约束条件如下：
1、对于所有的Ax Bx Cx，有 d[Bx] - d[Ax] <= Cx；
2、对于所有的Ay By Cy，有 d[By] - d[Ay] >= Cy；
3、然后根据我们的设定，有 d[x] >= d[x-1] + 1 (1 < x <= N) （这个条件是表示任何两个人的位置不重合）
而我们需要求的是d[N] - d[1]的最大值，即表示成d[N] - d[1] <= T，要求的就是这个T。
于是我们将所有的不等式都转化成d[x] - d[y] <= z的形式，如下：
1、d[Bx] - d[Ax] <= Cx
2、d[Ay] - d[By] <= -Cy
3、d[x-1] - d[x] <= -1
对于d[x] - d[y] <= z，令z = w(y, x)，那么有 d[x] <= d[y] + w(y, x)，所以当d[x] > d[y] + w(y, x)，我们需要更新d[x]的值，这对应了最短路的松弛操作，于是问题转化成了求1到N的最短路。
对于所有满足d[x] - d[y] <= z的不等式，从y向x建立一条权值为z的有向边。
然后从起点1出发，利用SPFA求到各个点的最短路，如果1到N不可达，说明最短路(即上文中的T)无限长，输出-2。如果某个点进入队列大于等于N次，则必定存在一条负环，即没有最短路，输出-1。否则T就等于1到N的最短路。

版权声明：本文为CSDN博主「英雄哪里出来」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/whereisherofrom/article/details/78922648

2.区间约束(P1986)

【例题2】给定n（n <= 50000）个整点闭区间和这个区间中至少有多少整点需要被选中，每个区间的范围为[ai, bi]，并且至少有ci个点需要被选中，其中0 <= ai <= bi <= 50000，问[0, 50000]至少需要有多少点被选中。
例如3 6 2 表示[3, 6]这个区间至少需要选择2个点，可以是3,4也可以是4,6（总情况有 C(4, 2)种 ）。

这类问题就没有线性约束那么明显，需要将问题进行一下转化，考虑到最后需要求的是一个完整区间内至少有多少点被选中，试着用d[i]表示[0, i]这个区间至少有多少点能被选中，根据定义，可以抽象出 d[-1] = 0，对于每个区间描述，可以表示成d[ bi ]  - d[ ai - 1 ] >= ci，而我们的目标要求的是 d[ 50000 ] - d[ -1 ] >= T 这个不等式中的T，将所有区间描述转化成图后求-1到50000的最长路。
  这里忽略了一些要素，因为d[i]描述了一个求和函数，所以对于d[i]和d[i-1]其实是有自身限制的，考虑到每个点有选和不选两种状态，所以d[i]和d[i-1]需要满足以下不等式：  0 <= d[i] - d[i-1] <= 1   （即第i个数选还是不选）
  这样一来，还需要加入 50000*2 = 100000 条边，由于边数和点数都是万级别的，所以不能采用单纯的Bellman-Ford ，需要利用SPFA进行优化，由于-1不能映射到小标，所以可以将所有点都向x轴正方向偏移1个单位（即所有数+1）。

版权声明：本文为CSDN博主「英雄哪里出来」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/whereisherofrom/article/details/78922648

3.未知条件约束

未知条件约束是指在不等式的右边不一定是个常数，可能是个未知数，可以通过枚举这个未知数，然后对不等式转化成差分约束进行求解。
【例题3】 在一家超市里，每个时刻都需要有营业员看管，R(i) (0 <= i < 24)表示从i时刻开始到i+1时刻结束需要的营业员的数目，现在有N(N <= 1000)个申请人申请这项工作，并且每个申请者都有一个起始工作时间 ti，如果第i个申请者被录用，那么他会连续工作8小时。 现在要求选择一些申请者进行录用，使得任何一个时刻i，营业员数目都能大于等于R(i)。
i = 0 1 2 3 4 5 6 … 20 21 22 23 23，分别对应时刻 [i, i+1)，特殊的，23表示的是[23, 0)，并且有些申请者的工作时间可能会“跨天”。
a[i] 表示在第i时刻开始工作的人数，是个未知量
b[i] 表示在第i时刻能够开始工作人数的上限， 是个已知量
R[i] 表示在第i时刻必须值班的人数，也是已知量

   那么第i时刻到第i+1时刻还在工作的人满足下面两个不等式（利用每人工作时间8小时这个条件）：
   当 i >= 7,        a[i-7] + a[i-6] + ... + a[i] >= R[i]                                     (1)
   当 0 <= i < 7,  (a[0] + ... + a[i]) + (a[i+17] + ... + a[23]) >= R[i]           (2)

   对于从第i时刻开始工作的人，满足以下不等式：
   0 <= i < 24,    0 <= a[i] <= b[i]                                                            (3)
   令 s[i] = a[0] + ... + a[i]，特殊地，s[-1] = 0
   上面三个式子用s[i]来表示，如下：
   s[i] - s[i-8] >= R[i]                               (i >= 7)                                      (1)
   s[i] + s[23] - s[i+16] >= R[i]               (0 <= i < 7)                                  (2)
   0 <= s[i] - s[i-1] <= b[i]                     (0 <= i < 24)                                (3)
   
  仔细观察不等式(2)，有三个未知数，这里的s[23]就是未知条件，所以还无法转化成差分约束求解，但是和i相关的变量只有两个，对于s[23]的值我们可以进行枚举，令s[23] = T, 则有以下几个不等式：
  
  s[i] - s[i-8] >= R[i]
  s[i] - s[i+16] >= R[i] - T
  s[i] - s[i-1] >= 0
  s[i-1] - s[i] >= -b[i]
  
  对于所有的不等式 s[y] - s[x] >= c，建立一条权值为c的边 x->y，于是问题转化成了求从原点-1到终点23的最长路。
  但是这个问题比较特殊，我们还少了一个条件，即：s[23] = T，它并不是一个不等式，我们需要将它也转化成不等式，由于设定s[-1] = 0，所以 s[23] - s[-1] = T，它可以转化成两个不等式：
  s[23] - s[-1] >= T
  s[-1] - s[23] >= -T
  将这两条边补到原图中，求出的最长路s[23]等于T，表示T就是满足条件的一个解，由于T的值时从小到大枚举的（T的范围为0到N），所以第一个满足条件的解就是答案。
  最后，观察申请者的数量，当i个申请者能够满足条件的时候，i+1个申请者必定可以满足条件，所以申请者的数量是满足单调性的，可以对T进行二分枚举，将枚举复杂度从O(N)降为O(logN)。

版权声明：本文为CSDN博主「英雄哪里出来」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/whereisherofrom/article/details/78922648