KNN从原理到实现

引文：决策树和基于规则的分类器都是积极学习方法（eager learner）的例子，因为一旦训练数据可用，他们就开始学习从输入属性到类标号的映射模型。一个相反的策略是推迟对训练数据的建模，直到需要分类测试样例时再进行。采用这种策略的技术被称为消极学习法（lazy learner）。最近邻分类器就是这样的一种方法。

注：KNN既可以用于分类，也可以用于回归。

1.K最近邻分类器原理

首先给出一张图，根据这张图来理解最近邻分类器，如下： 

 

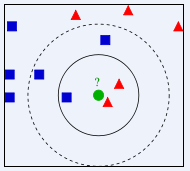
根据上图所示，有两类不同的样本数据，分别用 蓝色的小正方形 和 红色的小三角形 表示，而图正中间的那个 绿色的圆 所标示的数据则是待分类的数据。也就是说，现在， 我们不知道中间那个绿色的数据是从属于哪一类（蓝色小正方形or红色小三角形），下面，我们就要解决这个问题：给这个绿色的圆分类。

　　我们常说，物以类聚，人以群分，判别一个人是一个什么样品质特征的人，常常可以从他or她身边的朋友入手，所谓观其友，而识其人。我们不是要判别上图中那个绿色的圆是属于哪一类数据么，好说，从它的邻居下手。但一次性看多少个邻居呢？从上图中，你还能看到：

• 如果K=3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。
• 如果K=5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

于此我们看到，当无法判定当前待分类点是从属于已知分类中的哪一类时，我们可以依据统计学的理论看它所处的位置特征，衡量它周围邻居的权重，而把它归为(或分配)到权重更大的那一类。这就是K近邻算法的核心思想。其关键还在于K值的选取，所以应当谨慎。

KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

KNN 算法本身简单有效，它是一种 lazy-learning 算法，分类器不需要使用训练集进行训练，训练时间复杂度为0。KNN 分类的计算复杂度和训练集中的文档数目成正比，也就是说，如果训练集中文档总数为 n，那么 KNN 的分类时间复杂度为O(n)。

前面的例子中强调了选择合适的K值的重要性。如果太小，则最近邻分类器容易受到训练数据的噪声而产生的过分拟合的影响；相反，如果K太大，最近分类器可能会误会分类测试样例，因为最近邻列表中可能包含远离其近邻的数据点。（如下图所示） 

 
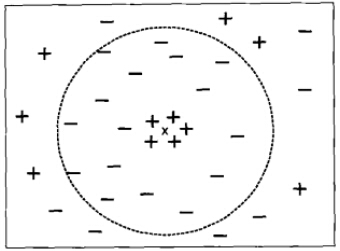
K较大时的最近邻分类 

可见，K值的选取还是非常关键。

---

2.算法

算法描述

k近邻算法简单、直观：给定一个训练数据集（包括类别标签），对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类，就把该输入实例分为这个类。下面是knn的算法步骤。

算法步骤如下所示：

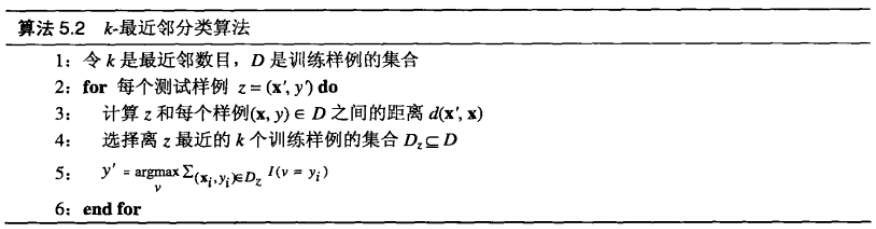
对每个测试样例 z=(x′,y′) ，算法计算它和所有训练样例 （x,y）属于D 之间的距离（如欧氏距离，或相似度），以确定其最近邻列表 Dz 。如果训练样例的数目很大，那么这种计算的开销就会很大。不过，可以使索引技术降低为测试样例找最近邻是的计算量。

特征空间中两个实例点的距离是两个实例相似程度的反映。

一旦得到最近邻列表，测试样例就可以根据最近邻的多数类进行分类，使用多数表决方法。

K值选择

k值对模型的预测有着直接的影响，如果k值过小，预测结果对邻近的实例点非常敏感。如果邻近的实例恰巧是噪声数据，预测就会出错。也就是说，k值越小就意味着整个模型就变得越复杂，越容易发生过拟合。

相反，如果k值越大，有点是可以减少模型的预测误差，缺点是学习的近似误差会增大。会使得距离实例点较远的点也起作用，致使预测发生错误。同时，k值的增大意味着模型变得越来越简单。如果k=N，那么无论输入实例是什么，都将简单的把它预测为样本中最多的一类。这显然实不可取的。

在实际建模应用中，k值一般取一个较小的数值，通常采用cross-validation的方法来选择最优的k值。

---

3.K最邻近算法实现（Python）

KNN.py（代码来源《机器学习实战》一书）

from numpy import *
import operator

class KNN:
    def createDataset(self):
        group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
        labels = ['A','A','B','B']
        return group,labels

    def KnnClassify(self,testX,trainX,labels,K):
        [N,M]=trainX.shape

    #calculate the distance between testX and other training samples
        difference = tile(testX,(N,1)) - trainX # tile for array and repeat for matrix in Python, == repmat in Matlab
        difference = difference ** 2 # take pow(difference,2)
        distance = difference.sum(1) # take the sum of difference from all dimensions
        distance = distance ** 0.5
        sortdiffidx = distance.argsort()

    # find the k nearest neighbours
        vote = {} #create the dictionary
        for i in range(K):
            ith_label = labels[sortdiffidx[i]];
            vote[ith_label] = vote.get(ith_label,0)+1 #get(ith_label,0) : if dictionary 'vote' exist key 'ith_label', return vote[ith_label]; else return 0
        sortedvote = sorted(vote.iteritems(),key = lambda x:x[1], reverse = True)
        # 'key = lambda x: x[1]' can be substituted by operator.itemgetter(1)
        return sortedvote[0][0]

k = KNN() #create KNN object
group,labels = k.createDataset()
cls = k.KnnClassify([0,0],group,labels,3)
print cls
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

---

运行： 
1. 在Python Shell 中可以运行KNN.py

>>>import os
>>>os.chdir("/home/liudiwei/code/data_miningKNN/")
>>>execfile("KNN.py")
 
 
1
2
3
 
 
1
2
3

输出:B 
（B表示类别）

2.或者terminal中直接运行

$ python KNN.py
 
 
1
 
 
1

3.也可以不在KNN.py中写输出，而选择在Shell中获得结果，i.e.,

>>>import KNN
>>> KNN.k.KnnClassify([0,0],KNN.group,KNN.labels,3)
 
 
1
2
 
 
1
2

References

【1】Introduction to Data Mining 数据挖掘导论 
【2】Rachel Zhang-K近邻分类算法实现 in Python

---

附件（两张自己的计算过程图）： 

图1 KNN算法核心部分 



图2 KNN计算过程