笔记：Matrix completion by Truncated Nuclear Norm Regularization

Zhang, D., Hu, Y., Ye, J., Li, X., & He, X. (2012, June). Matrix completion by truncated nuclear norm regularization. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2192-2199.
本文是这篇 CVPR 会议论文的笔记，主要是对文中的理论方法进行展开详解。本人学术水平有限，文中如有错误之处，敬请指正。
另外：这篇会议论文于 2013 年发表于 PAMI 期刊上，两篇 paper 的内容基本一致。
Hu, Y., Zhang, D., Ye, J., Li, X., & He, X. (2013). Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(9), 2117-2130.

摘要：估计视觉图像中缺失的值是计算机视觉中有挑战的问题，其可以被认为是一个低秩的近似问题。大部分的研究都是用核范数来代替秩操作。然而，在核范数最小化过程中，所有的奇异值一起被最小化，在实际中秩不能被很好地近似。此文提出了一种 Truncated Nuclear Norm Regularization (TNNR) 方法，只最小化较小的 $N − r$ 个部分奇异值，其中 $N$ 是奇异值的总个数，$r$ 是矩阵的秩。这样可以更好地近似矩阵的秩。此文更设计了两种高效的优化算法，alternating direction method of multipliers (ADMM) 和 accelerated proximal gradient line search (APGL) 方法。

1 简介

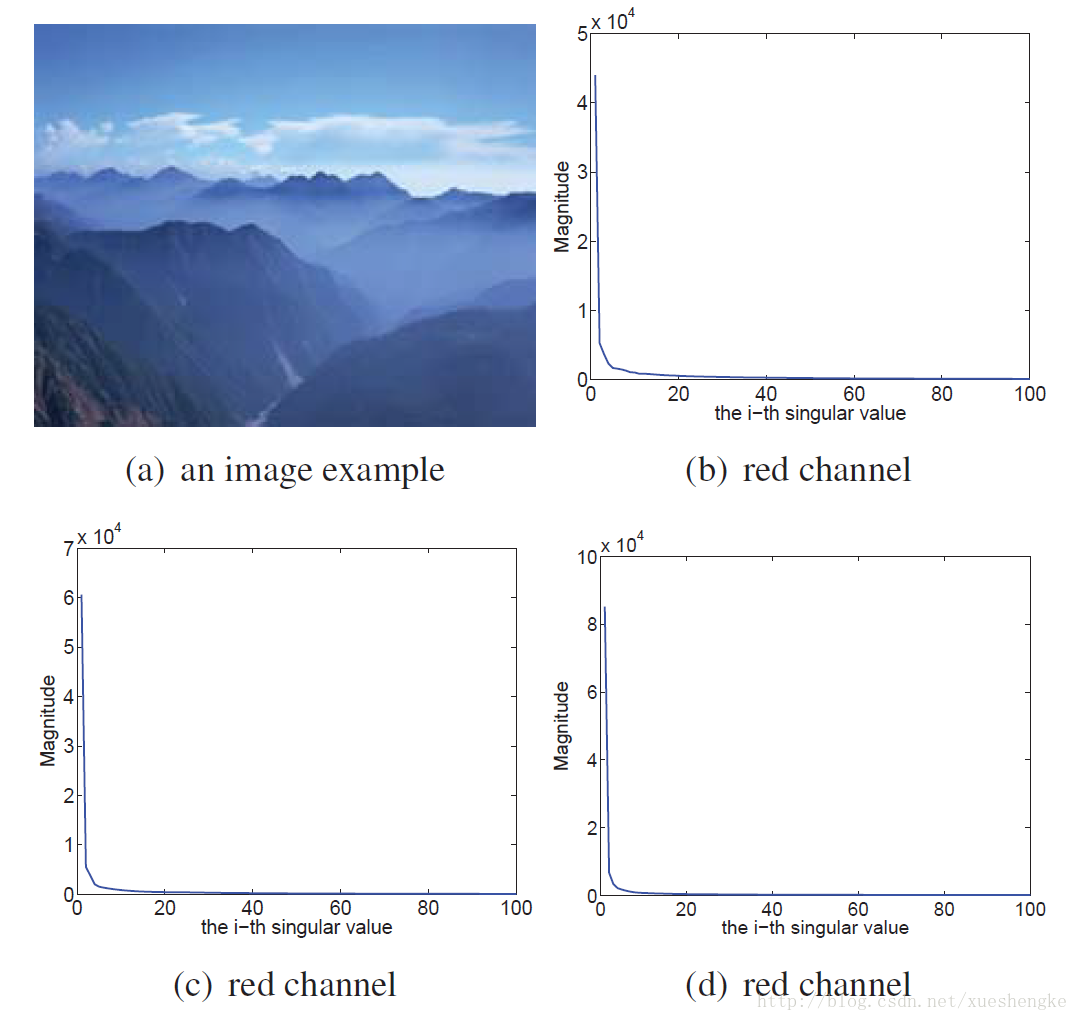
在许多的实际的计算视觉和模式识别中，比如图像恢复，数据中有丢失的部分。估计这些矩阵中丢失值得问题，即矩阵补全，已经受到了相当多的关注。视觉数据，，比如图像，有可能是低秩的，如图所示。于是，大部分的矩阵补全问题都旨在找到一个低秩的近似问题。具体的，给定一个不完整的数据 $\mathbf{M} \in \mathbb{R}^{m \times n}$，矩阵补全问题可被阐述为

$$\begin{equation} \begin{aligned} \min_{\mathbf{X}} \ & \qquad \text{rank}(\mathbf{X}) \\ \text{s.t.} \,\ & \mathbf{X}_{ij} = \mathbf{M}_{ij}, \ (i,j) \ \in \Omega, \end{aligned} \tag{1} \end{equation}$$
其中 $\mathbf{X} \in \mathbb{R}^{m \times n}$， $\Omega$ 是已知的元素的对应的位置集合。

然而， 以上的秩最小化问题是 NP-hard，因为其非凸性和不连续性。一种广泛采用的方法是核范数，即奇异值之和，作为一个凸的代替方法。受压缩感知的启发， Cand$\grave{e}$s 和 Recht 最近提出，如果矩阵的行空间和列空间是与标准基不一致的，那么核范数最小化可以恢复出矩阵，如果有足够的已知的元素。

已有的核范数方法，比如 singular value thresholding (SVT 1)，能够在无噪声的合成数据中获得较好的表现。然而，它们在真实的应用中不能得到低秩的解。这是因为核范数不能精确地近似秩函数。具体地，对比秩函数来说，所有的非零的奇异值都被平等处理，核范数则并不是。更差的是，这些方法优势甚至不收敛。因为核范数的理论的要求（比如不一致的性质）在实际中很难被满足。

此文提出了一种新的矩阵补全的方法，truncated nuclear norm regularization (TNNR)，来恢复矩阵中一些缺失的数据。于一般核范数的方法不同的是，并不是同时最小化所有奇异值的和，此文的方法仅最小化较小的 $\min(m,n)-r$ 个奇异值。这样，该方法可以获得一个更精确、鲁棒性的对秩函数的近似。此外，此文提出了两种简单的，高效的优化机制解决目标函数，即 alternating direction method of multipliers (ADMM) 2 和 accelerated proximal gradient line search method (APGL) 3 。

2 相关工作

稀疏表示，低秩矩阵分解相关，略

3 Truncated Nuclear Norm Regularization

令 $\mathbf{X}=(\mathbf{x},\cdots,\mathbf{x}_n)$ 成为一个 $m \times n$ 矩阵，$\Omega \subset\{1,\cdots,m\} \times \{1,\cdots,n\}$ 表示矩阵 $\mathbf{X}$ 中已知元素的索引，$\Omega^{\text{c}}$ 表示缺失元素的索引。可以方便的表示已知的元素

$$\begin{equation} (\mathbf{X}_{\Omega})_{ij} = \begin{cases} \mathbf{X}_{ij}, & \text{if } (i,j) \in \Omega, \\ 0, & \text{if } (i,j) \in \Omega^{\text{c}}. \end{cases} \tag{2} \end{equation}$$
正如之前描述的，核范数不能确保很好的近似秩函数在实际中。首先介绍一个定义
定义 3.1 给定一个矩阵 $\mathbf{X} \in \mathbb{R}^{m \times n}$，truncated nuclear norm $||\mathbf{X}||_r$ 定义为最小的 $\min(m,n)-r$ 个奇异值之和，也就是 $||\mathbf{X}||_r = \sum_{i=r+1}^{\min(m,n)} \sigma_i(\mathbf{X})$ 。于是，目标函数可以写为
$$\begin{align} \min_{\mathbf{X}} & \quad || \mathbf{X}||_r \\ \text{s.t.} & \ \ \mathbf{X}_\Omega = \mathbf{M}_\Omega. \tag{3} \end{align}$$
明显与传统的核范数不同，求解该问题一直可以得到低秩解，只要其存在。由于 $||\mathbf{X}||_r$ 是非凸的，不容易直接求解。于是，有如下的定义。
Theorem 3.1 对于给定的矩阵 $\mathbf{X} \in \mathbb{R}^{m \times n}$， $\mathbf{A} \in \mathbb{R}^{m \times m}$， $\mathbf{B} \in \mathbb{R}^{m \times n}$，和 $\mathbf{A} \mathbf{A}^\text{T} = \mathbf{I},\ \mathbf{B} \mathbf{B}^\text{T}=\mathbf{I}$。对于正的整数 $r \leq \min(m,n)$，我们有
$$\begin{equation} \text{tr} (\mathbf{A} \mathbf{X} \mathbf{B}^\text{T}) \leq \sum_{i=1}^{r} \sigma_i (\mathbf{X}). \tag{4} \end{equation}$$
证明 根据 Von Neumann 迹不等式，我们得到
$$\begin{equation} \text{tr} (\mathbf{A} \mathbf{X} \mathbf{B}^\text{T}) = \text{tr} (\mathbf{X} \mathbf{B}^\text{T} \mathbf{A}) \leq \sum_{i=1}^{\min(m,n)} \sigma_i (\mathbf{X}) \sigma_i (\mathbf{B}^\text{T} \mathbf{A}), \tag{5} \end{equation}$$
其中 $\sigma_1 (\mathbf{X}) \geq \cdots \geq \sigma_{\min(m,n)} (\mathbf{X}) \geq 0$ 。由于 $\text{rank} (\mathbf{A}) = r$， $\text{rank} (\mathbf{B}) = r$，所以有 $\text{rank} (\mathbf{B}^\text{T} \mathbf{A})=s \leq r$ 。对于 $i \leq s$， $\sigma_i(\mathbf{B}^\text{T} \mathbf{A}) > 0$ 和 $\sigma_i^2 (\mathbf{B}^\text{T} \mathbf{A})$ 是矩阵 $\mathbf{B}^\text{T} \mathbf{A} \mathbf{A}^\text{T} \mathbf{B} = \mathbf{B}^\text{T} \mathbf{B}$ 的第 $i$ 个特征值，也是 $\mathbf{B}^\text{T} \mathbf{B} = \mathbf{I}$ 的一个特征值。所以 $\sigma_i (\mathbf{B}^\text{T} \mathbf{A}) = 1$，对 $i=1,2,\cdots,r$，其余的都是 $0$ 。

∑i=1min(m,n)σi(X)σi(BTA)=∑i=1sσi(X)σi(BTA)+∑i=s+1min(m,n)σi(X)σi(BTA)=∑i=1sσi(X)⋅1+