【HDU4121】Xiangqi模拟象棋checkmate

Xiangqi

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3433    Accepted Submission(s): 831

Problem Description

Xiangqi is one of the most popular two-player board games in China. The game represents a battle between two armies with the goal of capturing the enemy’s “general” piece. In this problem, you are given a situation of later stage in the game. Besides, the red side has already “delivered a check”.  Your work is to check whether the situation is “checkmate”.

Now we introduce some basic rules of Xiangqi. Xiangqi is played on a 10×9 board and the pieces are placed on the intersections (points). The top left point is (1,1) and the bottom right point is (10,9). There are two groups of pieces marked by black or red Chinese characters, belonging to the two players separately. During the game, each player in turn moves one piece from the point it occupies to another point. No two pieces can occupy the same point at the same time. A piece can be moved onto a point occupied by an enemy piece, in which case the enemy piece is "captured" and removed from the board. When the general is in danger of being captured by the enemy player on the enemy player’s next move, the enemy player is said to have  "delivered a check". If the general's player can make no move to prevent the general's capture by next enemy move, the situation is called  “checkmate”.

We only use 4 kinds of pieces introducing as follows:
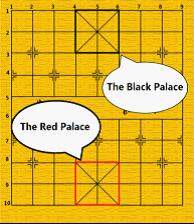
General: the generals can move and capture  one point either vertically or horizontally and cannot leave the “ palace” unless the situation called “ flying general” (see the figure above). “Flying general” means that one general can “fly” across the board to capture the enemy general if they stand on the same line without intervening pieces.
Chariot: the chariots can move and capture vertically and horizontally by any distance, but may not jump over intervening pieces
Cannon: the cannons move like the chariots, horizontally and vertically, but capture by jumping  exactly one piece (whether it is friendly or enemy) over to its target.
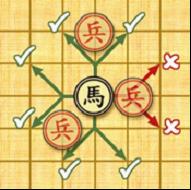
Horse: the horses have 8 kinds of jumps to move and capture shown in the left figure. However, if there is any pieces lying on a point away from the horse horizontally or vertically it cannot move or capture in that direction (see the figure below), which is called “ hobbling the horse’s leg”.



Now you are given a situation only containing a black general, a red general and several red chariots, cannons and horses, and the red side has delivered a check. Now it turns to black side’s move. Your job is to determine that whether this situation is “checkmate”.

 

Input

The input contains no more than 40 test cases. For each test case, the first line contains three integers representing the number of red pieces N (2<=N<=7) and the position of the black general. The following n lines contain details of N red pieces. For each line, there are a char and two integers representing the type and position of the piece (type char ‘G’ for general, ‘R’ for chariot, ‘H’ for horse and ‘C’ for cannon). We guarantee that the situation is legal and the red side has delivered the check.
There is a blank line between two test cases. The input ends by 0 0 0.

 

Output

For each test case, if the situation is checkmate, output a single word ‘YES’, otherwise output the word ‘NO’.

 

Sample Input

  
  

   
   2 1 4
G 10 5
R 6 4

3 1 5
H 4 5
G 10 5
C 7 5

0 0 0
  
  

 

Sample Output

  
  

   
   YES
NO


   
   

    
    

     
     Hint
    
    

    
    
     
     
    
     
In the first situation, the black general is checked by chariot and “flying general”.
In the second situation, the black general can move to (1, 4) or (1, 6) to stop check. 
See the figure above.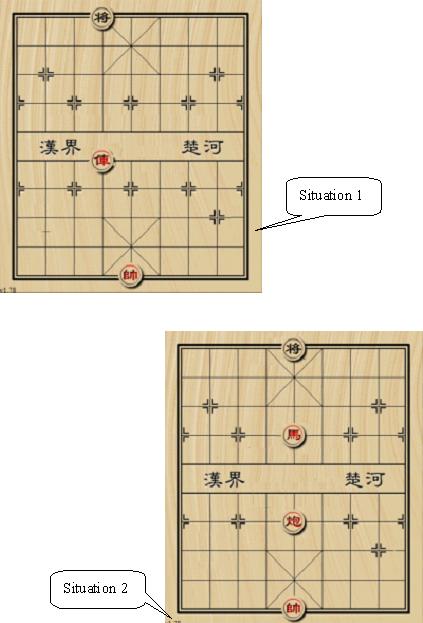

   
   
   
    
  
  

 

Source

2011 Asia Fuzhou Regional Contest

坑点有2

1： 黑棋可以走，而且必须走 ，走不了就算挂了！！！！尼玛，wa到死

2：黑棋可以杀红棋

起始状态可以不判

每次移动都进行判断即可

#define DeBUG
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <string>
#include <set>
#include <sstream>
#include <map>
#include <list>
#include <bitset>
using namespace std ;
#define zero {0}
#define INF 0x3f3f3f3f
#define EPS 1e-6
#define TRUE true
#define FALSE false
typedef long long LL;
const double PI = acos(-1.0);
inline int sgn(double x)
{
    return fabs(x) < EPS ? 0 : (x < 0 ? -1 : 1);
}
#define N 100005
int n, blackx, blacky;
int dirG[4][2] = {0, 1, 0, -1, 1, 0, -1, 0};
int dirH[8][2] = { -2, 1, -2, -1, -1, -2, 1, -2, 2, -1, 2, 1, 1, 2, -1, 2};
int dirHcheck[4][2] = { -1, 0, 0, -1, 1, 0, 0, 1};
char mp[12][12];
bool isb(int x, int y)
{
    if (x == blackx && y == blacky)
        return true;
    return false;
}
bool inborad(int x, int y)
{
    if (x > 0 && y > 0 && x <= 10 && y <= 9)
        return true;
    return false;
}
bool inboradblack(int x, int y)
{
    if (x >= 1 && x <= 3 && y >= 4 && y <= 6)
        return true;
    return false;
}
struct Node
{
    int x, y;
    char type;
    Node() {}
    Node(int a, int b, char c)
    {
        x = a;
        y = b;
        type = c;
    }
};
bool checkG(Node &n)
{
    for (int i = 0; i < 4; i++)
    {
        int x = n.x;
        int y = n.y;
        while (inborad(x, y))
        {
            x += dirG[i][0];
            y += dirG[i][1]; 
            if (isb(x, y))
            {
                return true;
            }
            if (mp[x][y] != 0)
                break;
        }
    }
    return false;
}
bool checkR(Node &n)
{
    for (int i = 0; i < 4; i++)
    {
        int x = n.x;
        int y = n.y;
        while (inborad(x, y))
        {
            x += dirG[i][0];
            y += dirG[i][1];
            if (isb(x, y))
            {
                return true;
            }
            if (mp[x][y] != 0)
                break;
        }
    }
    return false;
}
bool checkH(Node &n)
{
    int x = n.x;
    int y = n.y;
    int cx, cy;
    for (int i = 0; i < 8; i++)
    {
        x = n.x + dirH[i][0];
        y = n.y + dirH[i][1];
        cx = n.x + dirHcheck[i / 2][0];
        cy = n.y + dirHcheck[i / 2][1];
        // cout<<cx<<" "<<cy<<endl;
        if (inborad(x, y) && mp[cx][cy] == 0  && isb(x, y))
        {
            return true;
        }
    }
    return false;
}
bool checkC(Node &n)
{
    bool kill = false;
    for (int i = 0; i < 4; i++)
    {
        int x = n.x;
        int y = n.y;
        bool haskey = false;
        while (inborad(x, y))
        {
            x += dirG[i][0];
            y += dirG[i][1];
            if (isb(x, y) && haskey)
            {
                kill = true;
                break;
            }
            if (mp[x][y] != 0 && haskey)
            {
                break;
            }
            if (mp[x][y] != 0 && !haskey)
            {
                haskey = true;
                continue;
            }
           
        }
    }
    return kill;
}

Node nn[10];
bool cango[10];
bool checkall()
{
    bool kill = false;
    for (int i = 0; i < n; i++)
    {
        if (cango[i] == false)
            continue;
        if (nn[i].type == 'G')
        {
            kill = checkG(nn[i]);
            if (kill)
                break;
        }
        else if (nn[i].type == 'R')
        {
            kill = checkR(nn[i]);
            if (kill)
                break;
        }
        else if (nn[i].type == 'H')
        {
            kill = checkH(nn[i]);
            if (kill)
                break;
        }
        else
        {
            kill = checkC(nn[i]);
            if (kill)
                break;
        }
    }
    return kill;
}
bool checked()
{
    int prex = blackx;
    int prey = blacky;
    int can = 0;
    int checked = 0;
    for (int i = 0; i < 4; i++)
    {
        blackx = prex + dirG[i][0];
        blacky = prey + dirG[i][1];
        if (inboradblack(blackx, blacky))
        {
            can++;
            int j = 10;
            if (mp[blackx][blacky] != 0)
            {
                for (j = 0; j < n; j++)
                {
                    if (nn[j].x == blackx && nn[j].y == blacky)
                    {
                        cango[j] = false;
                        break;
                    }
                }
            }
            if (checkall())
                checked++;
            cango[j] = true;
        }
    }
    if (can == checked)
        return true;
    else
        return false;
}
int cnt=0;
int main()
{
#ifdef DeBUGs
    freopen("C:\\Users\\Sky\\Desktop\\1.in", "r", stdin);
#endif
    while (scanf("%d%d%d", &n, &blackx, &blacky), n || blacky || blackx)
    {
        char ty[100];
        int  x, y;
        memset(mp, 0, sizeof(mp));
        memset(nn, 0, sizeof(nn));
        for (int i = 0; i < n; i++)
        {
            scanf("%s%d%d", ty, &x, &y);
            nn[i].x = x;
            nn[i].y = y;
            nn[i].type = ty[0];
            mp[x][y] = ty[0];
            cango[i] = 1;
        }
        if (checked())
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}