[卡内基梅隆大学]10-725: Optimization Fall 2012 -Lecture 17: October 23 构造对偶函数

问题1：求解$l_{1,\infty}$范数子问题。

即求解在文献2中，有公式(10):

minw12||w−v||22+λ^||w||∞问题1

$$\min_{\mathbf w} \frac{1}{2} ||\mathbf w- \mathbf v||_2^2 +\hat{\lambda}||\mathbf w||_{\infty} \qquad 问题1$$ 因为二次函数的共轭是仍然是二次函数， $l_{\infty}$范数的共轭是 $l_1$障碍函数。因此得到公式（10）的对偶形式为如下公式(11)：
$$\begin{equation} \min_{\mathbf a}\frac{1}{2} ||\mathbf a-\mathbf v||_2^2 \\ s.t. ||\mathbf a||_1 \leq \hat \lambda \end{equation}$$
其中 $\mathbf a=\mathbf v-\mathbf w$.
公式(10)到公式（11）是怎么推导的呢？（由于 $\alpha$打不出矢量的形式（粗体），我们使用 $a$代替）
疑问：一说到函数的对偶，一般就是拉格朗日对偶，即有约束的函数才有对偶形式，公式(10）是无约束的情况，如何求解其对偶函数呢？
突破口:将无约束的问题转换为有约束的问题。从题中可以看到，公式（11）多了一个等式条件：$\mathbf a=\mathbf v-\mathbf w$.

解：
参照文献1中17.4.2 Dual construction via conjugates of pairs of functions
我们将公式(10)，引入约束$\mathbf a=\mathbf v-\mathbf w$，则$\mathbf w=\mathbf v-\mathbf a$,将其带入公式(10)中的第二个公式得到；

$$\begin{equation} \min_{\mathbf w，\mathbf a} \frac{1}{2} ||\mathbf w- \mathbf v||_2^2 +\hat{\lambda}||\mathbf v-\mathbf a||_{\infty} \\ s.t. \mathbf w=\mathbf v -\mathbf a \end{equation}$$
写成拉格朗日的形式为：
$$\begin{equation} g(u)=\min_{\mathbf w，\mathbf a} \frac{1}{2} ||\mathbf w- \mathbf v||_2^2 +\hat{\lambda}||\mathbf v-\mathbf a||_{\infty} +\mathbf u^T(\mathbf v-\mathbf w -\mathbf a) \end{equation}$$
进行变量的分解：
$$\begin{equation} g(u)={\color{red}{\min_{\mathbf w} \frac{1}{2} ||\mathbf w- \mathbf v||_2^2 -\mathbf u^T \mathbf w}}+{\color{blue}{\min_{\mathbf a}\hat{\lambda}||\mathbf v-\mathbf a||_{\infty} -\mathbf u^T (\mathbf a-\mathbf v)}} \end{equation}$$
转换为求最大值：
$$\begin{equation} g(u)={\color{red}{-\max_{\mathbf w} \mathbf u^T \mathbf w-\frac{1}{2} ||\mathbf w- \mathbf v||_2^2 }}-{\color{blue}{\max_{\mathbf a} \mathbf u^T (\mathbf a-\mathbf v)-\hat{\lambda}||\mathbf v-\mathbf a||_{\infty} }} \end{equation}$$
进行变量的替换，化简第二项：
$$\begin{equation} g(u)={\color{red}{-\max_{\mathbf w} \mathbf u^T \mathbf w-\frac{1}{2} ||\mathbf w- \mathbf v||_2^2 }}-{\color{blue}{\max_{\mathbf a} -\mathbf u^T (\mathbf v-\mathbf a)-\hat{\lambda}||\mathbf v-\mathbf a||_{\infty} }}\\ g(u)={\color{red}{-\max_{\mathbf w} \mathbf u^T \mathbf w-\frac{1}{2} ||\mathbf w- \mathbf v||_2^2 }}-{\color{blue}{\max_{\mathbf w} -\mathbf u^T (\mathbf w)-\hat{\lambda}||\mathbf w||_{\infty} }} \end{equation}$$
因此，由共轭函数的定义，上述可以表示成共轭形式，其中令 $f_1(\mathbf w)=\frac{1}{2}||\mathbf w-\mathbf v||_2^2$, $f_2(\mathbf a)=\hat \lambda ||\mathbf a||_{\infty}$：
$$\max_{\mathbf u}g(\mathbf u)=\max_{\mathbf u} -f_1^*(u)-f_2^*(-u)$$
即为：
$$arg\min_{\mathbf u}g(\mathbf u)=arg\min_{\mathbf u} f_1^*(u)+f_2^*(-u)$$

由2范数的平方的共轭函数是其本身，范数的共轭函数是其对偶范数单位球的示性函数[参见凸优化102页，例3.26]。并且由范数的性质：

$$||-x||=||x||$$
我们最终得到公式（11）。
还有一点是，函数 $f(x)=||x||$的共轭函数是：
$$\begin{equation} f^*(y)= \begin{cases} 0 &||y||_* \leq 1 \\ \infty & 其他情况 \end{cases} \end{equation}$$
那么函数 $f(x)=\lambda||x||$的共轭函数是:
$$\begin{equation} f^*(y)= \begin{cases} 0 &||y||_* \leq \lambda \\ \infty & 其他情况 \end{cases} \end{equation}$$
其可以通过参考： http://blog.csdn.net/raby_gyl/article/details/53178467
中的一维情况来理解（此时 $y,\lambda$均相当于线的斜率）。

问题2：求解$l_{1,2}$范数子问题

即求解问题：

minw12||w−v||22+λ^||w||2问题2

$$\min_{\mathbf w} \frac{1}{2}||\mathbf w-\mathbf v||_2^2 +\hat{\lambda}||\mathbf w||_2 \qquad 问题2$$
可能可行的求解方法：上面是关于 $\mathbf w$的二次函数，如果我们直接对 $f(\mathbf w)$关于 $\mathbf w$求偏导，然后令其等于0.
$$\frac{\partial f(\mathbf w)}{\partial \mathbf w}=\mathbf w-\mathbf v+\hat {\lambda} \frac{\mathbf w}{||\mathbf w||_2}=0$$
显然，通过上的公式我们很难化简出来 $\mathbf w$.
可行的方法: 和上面类似，我们引入一个等式约束，然后利用求解带有等式约束的拉格朗日对偶函数。
等式约束：
$$\mathbf a=\mathbf v-\mathbf w$$
同上面类似，范数平方的共轭是其本身，而范数的共轭是对偶范数在单位球上的示性函数，并且将最大化问题转化为共轭的问题，因此转化为下面的优化问题：
$$\begin{equation} \begin{aligned} \min_{\mathbf a}\frac{1}{2}||\mathbf a-\mathbf v||_2^2 \\ s.t. ||\mathbf a||_2 \leq \hat {\lambda} \end{aligned} \end{equation}$$
其中 $\mathbf a=\mathbf v-\mathbf w$。
很显然，如果 $||\mathbf v||_2 \leq \hat \lambda$，则 $\mathbf a=\mathbf v$,则 $\mathbf w=\mathbf v-\mathbf v=\mathbf 0$。
在观察一下公式问题2，假定存在一个 $\mathbf w^*$使得问题2最小化，并且 $\mathbf w^*$与 $\mathbf v$不共向，即不满足:
$$\mathbf w^* \neq k \mathbf v$$ ,则必然存在另外一个向量 $\mathbf w_0$，其大小和 $\mathbf w^*$相同，方向和 $\mathbf v$相同，即满足：
$$\mathbf w_0=\frac{\mathbf v}{||\mathbf v||_2}*||\mathbf w^*||$$ .
那么必有 $f(\mathbf w_0)<f(\mathbf w^*)$，与已知相矛盾，所以可得最优解 $\mathbf w^*$与 $\mathbf v$同方向，即满足:
$$\mathbf w^*=k\mathbf v$$
那么 $\mathbf a$也与 $\mathbf v$同向，即满足:
$$\mathbf a=k'\mathbf v$$

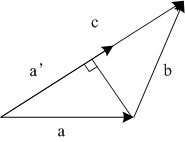
如上图，向量b=c-a,令向量c代表v,向量a代表w,那么我们总能找到一个a’,其大小与a相同，方向与c同向，可知道|c-a’|<|c-a|=|b|.
现在我们已知的条件有:
$$\begin{equation} \begin{aligned} \min_{\mathbf w}\frac{1}{2}||\mathbf a-\mathbf v||_2^2 \\ s.t. ||\mathbf a||_2 \leq \hat {\lambda} \\ \quad \mathbf a=k'\mathbf v \end{aligned} \end{equation}$$
我们可以通过画图的方式简单的求解：

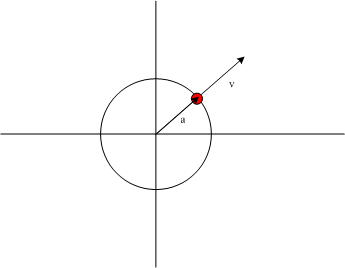
点 $\mathbf v$或者说向量 $\mathbf v$到圆内最近投影肯定在圆的边界上，并且投影后的矢量与 $\mathbf v$同向，即图中红色的点所示，其大小为圆的半径，其方向为 $\mathbf v$的方向，因此有：
$$\mathbf a=尺度*方向=\hat \lambda \frac{\mathbf v}{||\mathbf v||_2}$$
则 $\mathbf w=\mathbf v-\hat \lambda \frac{\mathbf v}{||\mathbf v||}$.
因此最后的最优解为：
$$\begin{equation} \mathbf w*= \begin{cases} \left ( 1- \frac{\hat \lambda}{||\mathbf v||_2} \right ) \mathbf v &||\mathbf v||_2 > \hat \lambda \\ \mathbf 0 & ||\mathbf v||_2 \leq \hat \lambda \end{cases} \end{equation}$$

参考文献：
1. 10-725: Optimization Fall 2012
Lecture 17: October 23
Lecturer: Geoff Gordon/Ryan Tibshirani Scribes: Yifei Ma, Mahdi Pakdaman Naeini
2. Accelerated Gradient Method for Multi-Task Sparse Learning Problem