简谈并查集 By angry_snail
一.并查集简介
二.路径压缩
三.并查集的应用
四.并查集的离线算法
五.带权并查集
六.可持久化并查集
一并查集简介
并查集是一种抽象的数据结构。其操作对象为集合。并:给出两个元素,若
个元素不在同一个集合当中,则合并两个元素所在的集合 查:给出两个元素,询问这两个元素是否在同一个集合当中。
引题 1(poj 2524)宗教信仰:
给出m对关系,没对关系x,y表示这两人信仰同一个宗教,每人仅信仰一个宗教。问这n个人最多信仰多少个宗教?
传统思路:
N个人相当于n个集合,每个集合标号id[i]=i;当输入一组关系时,我们先看这两个人的id是否一样。不一样就选择其中一个为标准,遍历一下n个人,将属于另一个集合的人的id全部修改。最后统计有n个人有多少个不同的id就可以了。
主要代码
Void fun()
{
for(int i=1;i<=n;i++)id[i]=i;
for(int i=1;i<=m;i++)
scanf(x,y);
if(id[x]!=id[y])
for(j=1;j<=n;j++)
if(id[j]==id[x])id[j]=id[y];
for(int i=1;i<=n;i++)
if(!h[id[i]])ans++,h[id[i]]=1;
}
可以看出,最坏情况下每次都要遍历一遍,时间复杂度为O(n*m);在数据大的时候难以接受;
并查集思路:
并查集采用树的方式来实现:
用father[x]来表示与x在同一个集合的上一个元素,每个元素有且仅有一个直接父亲。初始化f[i]=I;
图一.

合并过程:
- 1 2合并 f[2]=1;
- 1 3 合并 f[3]=1;
- 4 5 合并 f[4]=5;
- 3 5 合并 f[5]=3;
相关代码:
void find(int x)
If(f[x]!=x)return find(f[x])l
return x;
void unionn(int x,int y);
if(find(x)!=find(y))f[x]=y;
效率分析:
合并时间为O(1),查找O(L),L为路径上点的个数。有时数据极端树会退化为链,即为O(n). 总时间复杂度O(n*m); 可以看出,和暴力法的集合操作时间一致;
因此需要优化;
二并查集的路径压缩
在图一第4步的合并中我们可以这样做:当要合并3 5 所在的集合时,我们不要直接将3 5合并,而是去找3 5所在集合的根节点,即1 5。我们不要直接让5指向3,而是指向它的根节点1. 并且在查找的时候把路径上的点都指向根节点。从图中可以看出,节点5直接指向根节点1,这样就减少了链的长度。
虽然1-5-4长度为3,但每次查询时都会进行路径压缩,使得链的长度很小。
可以证明这样操作每次查询的时间是个常数(然而我不会证)
图二
图
故代码
Void find(int x)
If(f[x]!=x)f[x]=find(f[x]); //递归结束时将f[x]指向所在集合的根节点
return f[x];
void unionn(int x,int y)
x=find(x),y=find(y); //找到各自集合的根节点
if(x!=y)f[x]=y;
最后带上本例题的代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=50001+10;
int n,m,tot;
int f[N],h[N];
int find(int x)
{
return f[x]=f[x]==x?x:find(f[x]);
}
int main()
{
while(1)
{
scanf("%d%d",&n,&m);
if(n==0&&m==0)break;
for(int i=0;i<=n;i++)f[i]=i,h[i]=0;
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
x=find(x);y=find(y);
if(x!=y)f[x]=y;
}
int ans=0;
for(int i=1;i<=n;i++)
{
int t=find(i);
if(!h[t])
{
ans++;
h[t]=1;
}
}
tot++;
printf("Case %d: %d\n",tot,ans);
}
return 0;
}
三并查集的应用
1. kruskal求最小生成树
思路:首先将边从小到大排序,若两点不在同一生成树中,则加边,合并两点所在的集合。至到选取完n个点。
2. CodeForces 915F
题意:给定一颗树求 ,其中I(I,j)表示节点I,j路径中最大值与最小值之差。n<=1e6.
**思路:**暴力法是枚举ij,再加上遍历两点间的路径,时间复杂度O(nnn)
分析求i(I,j),可以拆分成sum_max(I,j)-sum_min(I,j)两个部分。现在单独考虑如何求sum_max(I,j); 先建图,如下图所示。考虑最小的边2对答案的影响。可以看出只有1,4节点经过这条边权为2的点。Sum+=112。再考虑第二小的边3,可以看出节点3和1,2所在集合中的元素都会经过这条最大边,因此答案贡献为sum+=123。所以可以得到这样一个算法,将边从小到大排序,对于每条边对答案的影响为其两边集合中点的数量之积再乘以边权值。对于求sum_min就需要对边按照从大到小排序。同理可求。

代码如下:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e6+10;
int n;
int a[N],f[N],c[N],xi[N],yi[N];
struct node
{
int next,u,v,d;
bool operator < (const node &x)const
{
return d<x.d;
}
}edge[N];
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
f[i]=i;
c[i]=1;
}
for(int i=1;i<=n-1;i++)scanf("%d%d",&xi[i],&yi[i]);
for(int i=1;i<=n-1;i++) //加边
{
int u=xi[i],v=yi[i];
edge[i].u=u;edge[i].v=v;
edge[i].d=max(a[u],a[v]);
}
long long int maxx=0;
sort(edge+1,edge+n); //从小到大排序
for(int i=1;i<=n-1;i++) //计算每条边的贡献
{
int u=edge[i].u,v=edge[i].v,d=edge[i].d;
u=find(u);v=find(v);
if(u!=v)
{
f[u]=v;
//printf("%d %d %d %d %d--\n",u,v,d,c[u],c[v]);
maxx+=(long long int)c[u]*c[v]*d;
c[v]+=c[u];
}
}
//printf("%d++\n",maxx);
for(int i=1;i<=n;i++)
{
f[i]=i;
c[i]=1;
}
//求sum_min
for(int i=1;i<=n-1;i++) //加边
{
int u=xi[i],v=yi[i];
edge[i].u=u;edge[i].v=v;
edge[i].d=min(a[u],a[v]);
}
long long int minn=0;
sort(edge+1,edge+n); //从小到大排序
for(int i=n-1;i>=1;i--) //从大到小取边
{
int u=edge[i].u,v=edge[i].v,d=edge[i].d;
u=find(u);v=find(v);
if(u!=v)
{
f[u]=v;
minn+=(long long int)c[u]*c[v]*d;
c[v]+=c[u];
}
}
//printf("%d--\n",minn);
printf("%I64d\n",maxx-minn);
}
return 0;
}
四.并查集与离线算法
**离线算法:**所谓的离线算法,就是对于多组询问,每次的询问不会改变原先的数据。因而,可以将每次询问保存下来。1.进行集体处理,像上面一题就是进行集体处理,但是并没有多组询问。2.改变处理询问的次序,算法效率也会提升一个档次。
1. 并查集在lca中的应用 tarjan
对于一棵有根树,m次询问。每次询问两个点的最近公共祖先是节点几
思路:暴力法:建完树后,根据两个点的深度关系一步一步往上爬
优化:倍增
方法二:tarjan算法
基本思想:对一颗树进行bfs,当递归结束时,标记并将其与其父亲加到同一个并查集集合中,父亲节点在并查集树中同样是父亲。再遍历改点的询问,如果另一个节点也被遍历过了,那么最近公共祖先就是另一个节点所在并查集集合的根节点。如图所示:假设遍历完6号节点(已经遍历的用黑点圈出),假设有询问6,2,则答案为2所在并查集的根节点1.
又假设6,7,则lca为6.又假设6,3,由于3还没有被遍历,所以没输出。
等到回溯到3时。有询问3,6,则lca为6所在集合的根节点3.
代码如下:
**
#include<cstdio>
#include<algorithm>
using namespace std;
cons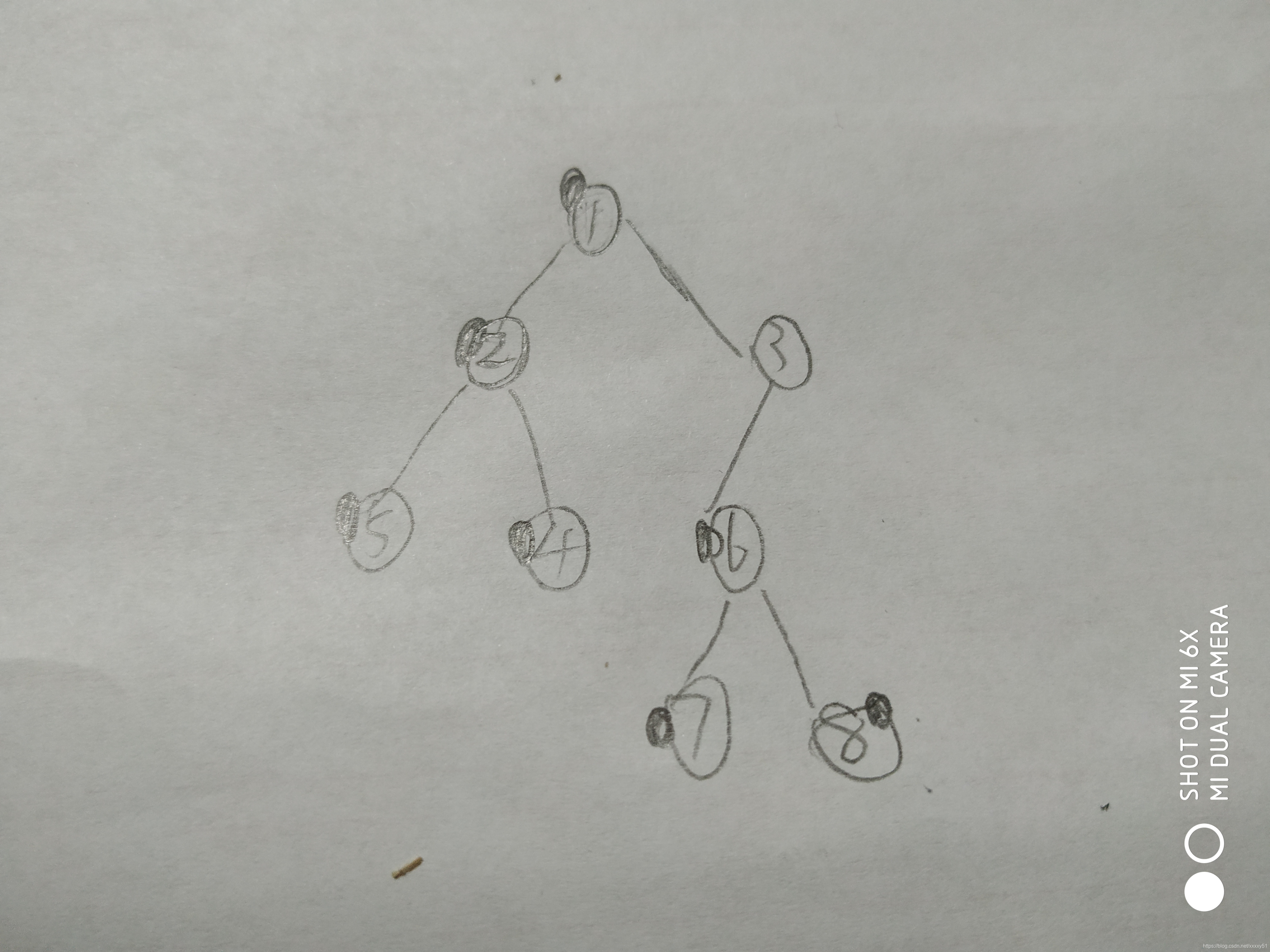t int N=10001;
int n,m,s,nl;
int hd[N],h[N],f[N],vis[N],ans[N];
struct node
{
int u,v,id,next;
}edge[N],e[N];
void add_edge(int u,int v)
{
edge[++nl].next=hd[u];
edge[nl].u=u;
edge[nl].v=v;
hd[u]=nl;
}
void add_node(int u,int v,int id)
{
e[++nl].next=h[u];
e[nl].u=u;
e[nl].v=v;
e[nl].id=id;
h[u]=nl;
}
int find(int x)
{
return f[x]==x?x:find(f[x]);
}
void dfs(int u,int fa)
{
for(int i=hd[u];i;i=edge[i].next)
{
int v=edge[i].v;
if(v!=fa)dfs(v,u);
}
vis[u]=1;
for(int j=h[u];j;j=e[j].next)
{
int to=e[j].v,id=e[j].id;
if(vis[to])ans[id]=find(to);
}
f[u]=fa;
}
int main()
{
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=n;i++)f[i]=i;
for(int i=1;i<=n-1;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add_edge(u,v);
add_edge(v,u);
}
nl=0;
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add_node(u,v,i);
add_node(v,u,i);
}
dfs(s,s);
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
return 0;
}
**
2. 星球大战
**题意:**给定一个n点m边的图,k次操作,每次摧毁一个点,求每次过后联通块的个数。
**分析:*暴力:对于一个图每次消除一个点后,要将和这个点连接的所有点的边都删除,重新建图,然后dfs一遍求联通块。时间k(m+n);
并查集:对于k次操作,每次消除一个点,如果每次消除的都不一样,那么k次过后还剩下n-k个点是在一个或多个联通块中。那我们先把这k个点用并查集合并。然后从后往前加点,若边的两点不在同一连通块中,则合并,连通块数-1。否则跳过。保存到答案数组里。时间o(k*a)a为并查集常数。
**比较:**正向处理时删边后会多x个联通块,要重新建图。而反向处理时,每次加边,答案至多-1.省去了判断和建图的时间。
代码如下:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=4e5+10;
int n,m,k,nl,tot,last;
int a[N],b[N],fa[N],ans[N],vis[N],hd[N];
struct node
{
int u,v,next;
}edge[N*2];
void add_edge(int u,int v)
{
edge[++nl].next=hd[u];
edge[nl].u=u;edge[nl].v=v;
hd[u]=nl;
}
int findx(int x)
{
return fa[x]==x?x:fa[x]=findx(fa[x]);
}
void dfs()
{
for(int i=0;i<n;i++)fa[i]=i;
for(int i=0;i<n;i++)
if(!b[i])
{
for(int j=hd[i];j;j=edge[j].next)
{
int v=edge[j].v;
if(b[v])continue;
int x=findx(i),y=findx(v);
if(x!=y)
{
fa[x]=y;
}
}
}
for(int i=1;i<=n;i++)fa[i]=findx(i);
for(int i=0;i<n;i++)
if(!b[i]&&!vis[fa[i]])
{
tot++;
vis[fa[i]]=1;
}
}
void kruskal()
{
for(int i=k;i>=1;i--)
{
tot++;//printf("%d --",tot);
b[a[i]]=0;
int u=a[i];//printf("%d %d--\n",i,u);
for(int j=hd[u];j;j=edge[j].next)
{
int v=edge[j].v;
if(b[v])continue; //v已被摧毁
int x=findx(u),y=findx(v);
if(x!=y)
{
fa[x]=y;
tot--;
}//printf("%d %d %d %d**++\n",i,u,v,tot);
}
ans[i]=tot;
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add_edge(u,v);
add_edge(v,u);
}
scanf("%d",&k);
for(int i=1;i<=k;i++)
{
scanf("%d",&a[i]);
b[a[i]]=1; //要摧毁的点
}
dfs();last=tot;
kruskal();
for(int i=1;i<=k;i++)
printf("%d\n",ans[i]);
printf("%d\n",last);
return 0;
}
五.带权并查集
**带权并查集:**普通的并查集只要求两个节点之间所在集合的关系。而带权并查集则是给每条边赋予一个权值。带权并查集既要维护节点间的关系,又要考虑到边权值对结果的影响。比如说:
1. noi2002 银河英雄传说
题目描述:有n列战舰,T次操作。(1).将战舰i合并到战舰上。(2)询问战舰I,j之间有多少战舰,若两个战舰不在一列上,则输出-1。
分析:判断I,j是否在同一个集合中,显然可以用并查集来实现。现在又要求同一个集合中两节点间的距离。我们可以设一个数组front[i]表示i节点到并查集根结点的距离。Num[i]表示当前列的战舰的个数。在路径压缩时,我们可以先纪录一个节点的父亲节点,当回缩时父亲节点指向根节点,但我们保留了原先的父亲节点t。因此,根据前缀和思想front[x]+=front[t];
查找代码:
int find(int n){
if(fa[n]==n)return fa[n];
int fn=find(fa[n]);
front[n]+=front[fa[n]];
return fa[n]=fn;
}
**合并操作时:**设x合并到y,先找到根节点x=find(x),y=find(y);
则y作为新集合的根节点。X插入到y的尾部,其front值要加上num[y]
集合的大小num[y].之后num[x]=0.这个新的集合只有根节点的num值非0,表示当前集合的大小。以后更新的过程中也是如此。
总代码:
#include<bits/stdc++.h>
using namespace std;
int fa[30001],front[30001],num[30001],x,y,i,j,n,T,ans;
char ins;
int find(int x)
{
if(fa[x]==x)return x;
int t=fa[x];
fa[x]=find(fa[x]);
front[x]+=front[t];
return fa[x];
}
int main()
{
cin>>T;
for(i=1;i<=30000;++i)
{
fa[i]=i;
front[i]=0;
num[i]=1;
}
while(T--)
{
cin>>ins>>x>>y;
int fx=find(x);
int fy=find(y);
if(ins=='M')
{
front[fx]+=num[fy];
fa[fx]=fy;
num[fy]+=num[fx]; //新集合大小
num[fx]=0;
}
if(ins=='C')
{
if(fx!=fy)cout<<"-1"<<endl;
else cout<<abs(front[x]-front[y])-1<<endl;
}
}
return 0;
}
2. HihoCoder-1515-分数调查
输入
第一行包含三个整数N, M和Q。N表示学生总数,M表示小Hi知道消息的总数,Q表示小Hi想询问的数量。
以下M行每行三个整数,X, Y和S。表示X号同学的分数比Y号同学的分数高S分。
以下Q行每行两个整数,X和Y。表示小Hi想知道X号同学的分数比Y号同学的分数高几分。
对于50%的数据,1 <= N, M, Q <= 1000
对于100%的数据,1 <= N, M, Q<= 100000 1 <= X, Y <= N -1000 <= S <= 1000
数据保证没有矛盾。
输出
对于每个询问,如果不能判断出X比Y高几分输出-1。否则输出X比Y高的分数。
**分析:**此题和上题差不多。查找操作一样。合并时要将a=find(x),b=find(y),把a连接到b上。其front[a]=front[y]-front[x]+s;s表示x比y高s分。查询时直接减下就行。(代码略)
小结:带权并查集求和的题型只需要在路径压缩时处理好和,在合并的时候正确的将两个节点间的信息“缝合”就行了。
六.可持久化并查集
** 我不会**
























 2047
2047











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








