手搓传染病模型（SEI）

在公共卫生与传染病研究领域，数学模型是理解疾病传播规律的强大工具。今天，我们就来通过 MATLAB 代码，深入探索 SEI 模型，看看如何模拟流行病的传播过程。

📌模拟参数设置

首先，设定初始比例：

• S₀ = 0.99：表示 99% 的人群初始为易感者，对疾病没有免疫力。
• E₀ = 0：初始没有暴露者（已感染但未具备传染性）。
• I₀ = 0.01：1% 的人群初始为感染者，作为疾病传播的 “源头”。 将这些初始条件组合成向量 init = [S₀; E₀; I₀]。 时间范围 tspan = 0:80，意味着我们将模拟 80 天内的传播情况，每天记录一个数据点。

🔢模型参数定义

• β = 0.8：传染率，反映感染者将疾病传播给易感者的能力。数值越高，传播越快。
• ω = 0.1：潜伏期转化率，即暴露者转为感染者的速率。

🧮求解微分方程

利用 MATLAB 的 ode45 函数求解 SEI 模型的微分方程组。这里的匿名函数 @(t, y) SEI_ode(t, y, β, ω) 定义了微分方程的形式（假设 SEI_ode 函数已正确实现，描述 S、E、I 随时间的变化率）。将初始条件 init 代入，即可得到各时间点的 S、E、I 数值。

% 模拟参数设置
S0 = 0.99;   % 初始易感者比例
E0 = 0;      % 初始暴露者比例
I0 = 0.01;   % 初始感染者比例
init = [S0; E0; I0];  % 初始条件向量

tspan = 0:80; % 时间范围（0到80天，每天一个点）

% 模型参数
beta = 0.8;   % 传染率
omega = 0.1;  % 潜伏期转化率

% 求解微分方程
[~, y] = ode45(@(t, y) SEI_ode(t, y, beta, omega), tspan, init);

% 提取结果
S = y(:, 1);
E = y(:, 2);
I = y(:, 3);

% 绘制结果
figure;
plot(tspan, S, 'Color', [0.3922, 0.5843, 0.9294], 'LineWidth', 1.5); % 易感者
hold on;
plot(tspan, E, 'Color', [1, 0.5, 0], 'LineWidth', 1.5);            % 暴露者
plot(tspan, I, 'Color', [0.5451, 0, 0], 'LineWidth', 1.5);         % 感染者

% 图表美化
xlabel('时间（天）');
ylabel('人数比例');
title('SEI模型：流行病传播模拟');
legend('易感者 (S)', '暴露者 (E)', '感染者 (I)', 'Location', 'best');
grid on;
set(gca, 'FontName', 'Microsoft YaHei');  % 设置中文字体（根据系统调整）
hold off;

% 定义SEI模型的微分方程
function dydt = SEI_ode(t, y, beta, omega)
    S = y(1);
    E = y(2);
    I = y(3);
    
    % 各群体变化率
    dSdt = -beta * S * I;       % 易感者变化率
    dEdt = beta * S * I - omega * E; % 暴露者变化率
    dIdt = omega * E;            % 感染者变化率
    
    dydt = [dSdt; dEdt; dIdt];
end

 

📊提取与可视化结果

从解 y 中提取三列数据，分别对应易感者（S）、暴露者（E）、感染者（I）。 绘图部分是亮点：

• 用不同颜色区分：
  • 易感者（S）：清新的蓝色 [0.3922, 0.5843, 0.9294]，象征未受感染的 “纯净” 状态。
  • 暴露者（E）：醒目的橙色 [1, 0.5, 0]，代表处于潜伏期的 “过渡” 状态。
  • 感染者（I）：深沉的红色 [0.5451, 0, 0]，凸显疾病感染的 “危险” 状态。
• 添加清晰的标签 xlabel (' 时间（天）')、ylabel (' 人数比例 ')，以及标题 title ('SEI 模型：流行病传播模拟 ')，让图表主题一目了然。 - 通过 legend 函数添加图例，注明各曲线含义，并设置 'Location', 'best' 自动选择最佳显示位置。
• grid on 显示网格，辅助观察数据变化趋势。
• set(gca, 'FontName', 'Microsoft YaHei') 确保中文显示正常（可根据系统调整字体）。

🌟图表背后的意义

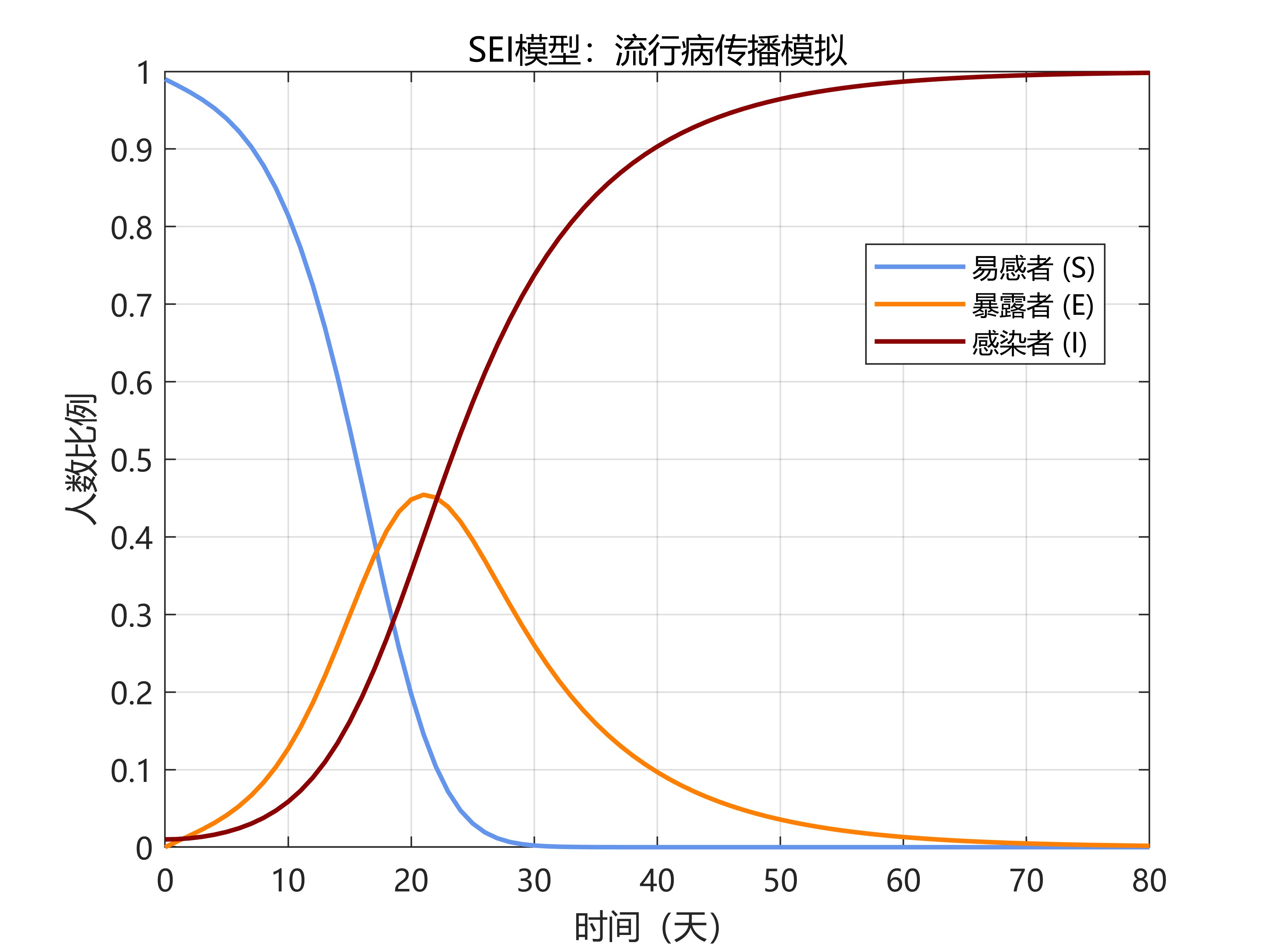
通过这张图，我们能直观看到：

• 易感者（S）随时间逐渐减少，因为不断被感染，这体现了疾病的传播对易感人群的消耗。
• 暴露者（E）先增加后减少，反映了潜伏期人群的动态变化 —— 初期感染后进入潜伏期的人增多，后期逐渐转为感染者。
• 感染者（I）的变化趋势，受传染率（β）和潜伏期转化率（ω）共同影响。若 β 增大，感染者上升速度会加快；若 ω 增大，暴露者转为感染者的时间缩短，曲线形态也会改变。

📌注意事项

• 确保 SEI_ode 函数正确定义微分方程（如：\(\frac{dS}{dt} = -\beta S I\)，\(\frac{dE}{dt} = \beta S I - \omega E\)，\(\frac{dI}{dt} = \omega E\)），否则求解会出错。
• 参数调整：修改 β 和 ω，观察传播趋势如何变化。例如，降低 β（如采取隔离措施），可明显看到感染者增长放缓，这对模拟公共卫生政策的效果极具价值。

SEI 模型虽简化了现实（如未考虑康复和免疫），但为我们理解流行病传播提供了基础框架。通过 MATLAB 代码，我们能快速模拟不同参数下的传播情况，为进一步研究更复杂的模型（如 SEIR）打下基础。快来动手试试，调整参数，看看疫情趋势如何变化吧！ 💻🦠