地理数据处理实战：从城市坐标到距离矩阵的可视化分析-CSDN博客

本文链接：https://blog.csdn.net/xyhxx99499/article/details/148100845

在数据分析与地理信息处理中，计算空间距离并可视化城市间的关联是基础却关键的任务。今天，我们以中国 5 个典型城市（北京、上海、广州、成都、杭州）为例，演示如何用 MATLAB 高效计算球面距离矩阵，并通过地理分布图和热力图直观呈现数据特征。代码巧妙运用向量化运算和条件判断，兼顾专业性与可读性，快跟我一起解锁地理数据的 “空间密码” 吧～😉

一、数据准备：构建城市坐标 “数据库” 🏙️

1. 城市经纬度初始化

vertexs = [
    116.40, 39.90;   % 北京
    121.47, 31.23;   % 上海
    113.26, 23.12;   % 广州
    104.06, 30.67;   % 成都
    120.15, 30.28;   % 杭州
];

直接按顺序输入城市的经度和纬度（单位：度），形成5×2矩阵vertexs
包含北方（北京）、东部（上海、杭州）、南部（广州）、西部（成都）城市，覆盖全国主要区域

二、距离计算：用向量化运算高效求解球面距离 🌍

1. 大圆距离公式（球面距离计算）

地球近似为球体时，两点间最短距离（大圆距离）公式为：\(d = R \cdot 2 \arcsin\left( \sqrt{\sin^2(\Delta\phi/2) + \cos\phi_1 \cos\phi_2 \sin^2(\Delta\lambda/2)} \right)\) 其中：

\(R = 6378.137 \, \text{km}\) 为地球半径
\(\Delta\phi\) 为纬度差，\(\Delta\lambda\) 为经度差

2. 向量化代码实现（避免循环，提升效率）

lon = vertexs(:,1);  % 提取经度（x轴）
lat = vertexs(:,2);  % 提取纬度（y轴）

% 计算经纬度差（矩阵运算实现两两相减）
dlon = lon' - lon;  % 经度差矩阵（5×5），每行是某城市与所有城市的经度差
dlat = lat' - lat;  % 纬度差矩阵

% 代入大圆距离公式（向量化计算每个元素）
a = sin(dlat/2).^2 + cos(lat') .* cos(lat) .* sin(dlon/2).^2;
h = 2 * atan2(sqrt(a), sqrt(1-a));  % 计算弧度距离
dist = 6378.137 * h;  % 转换为千米

核心技巧：利用矩阵运算替代双重循环，计算复杂度从 \(O(n^2)\) 优化为向量操作，适合大规模数据
结果：得到5×5距离矩阵dist，例如dist(1,2)表示北京到上海的距离

三、可视化呈现：让数据 “地图化” 与 “热力化” 📊

1. 地理分布图：直观展示城市位置关系

try
    % 尝试使用Mapping Toolbox绘制带地图背景的可视化
    figure;
    geoscatter(lat, lon, 100, 'filled', 'MarkerFaceColor', 'r');  % 绘制地理散点
    geobasemap('streets');  % 添加街道地图背景
    title('城市地理位置分布');
    % 添加城市名称标签（注意经纬度顺序：geoscatter输入为[lat, lon]）
    text(lat, lon, {'北京','上海','广州','成都','杭州'},
         'VerticalAlignment','bottom', 'FontWeight','bold');
catch
    % 若未安装Mapping Toolbox，使用普通二维图
    figure;
    plot(lon, lat, 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');  % 二维散点图
    xlabel('经度 (°)'); ylabel('纬度 (°)'); 
    title('城市地理位置分布');
    text(lon, lat, {'北京','上海','广州','成都','杭州'},
         'VerticalAlignment','bottom', 'FontWeight','bold');
    grid on;
end

智能兼容：通过try-catch自动判断是否使用专业地图工具，确保代码可移植
细节处理：标签垂直对齐设为bottom，避免遮挡标记点；字体加粗增强可读性

2. 距离矩阵热力图：量化城市间的空间关联

figure;
imagesc(dist);  % 绘制热力图（颜色越深距离越远）
colorbar;  % 添加颜色标尺
title('城市间距离矩阵 (km)');

% 设置坐标轴标签（45度倾斜避免重叠）
cities = {'北京', '上海', '广州', '成都', '杭州'};
set(gca, 'XTick',1:5, 'XTickLabel',cities, 'XTickLabelRotation',45);
set(gca, 'YTick',1:5, 'YTickLabel',cities);

% 叠加具体距离数值（四舍五入到整数）
for i = 1:5
    for j = 1:5
        text(j, i, sprintf('%.0f', dist(i,j)),
             'HorizontalAlignment','center');  % 居中对齐
    end
end
colormap hot;  % 使用热图配色方案（红色系突出远距离）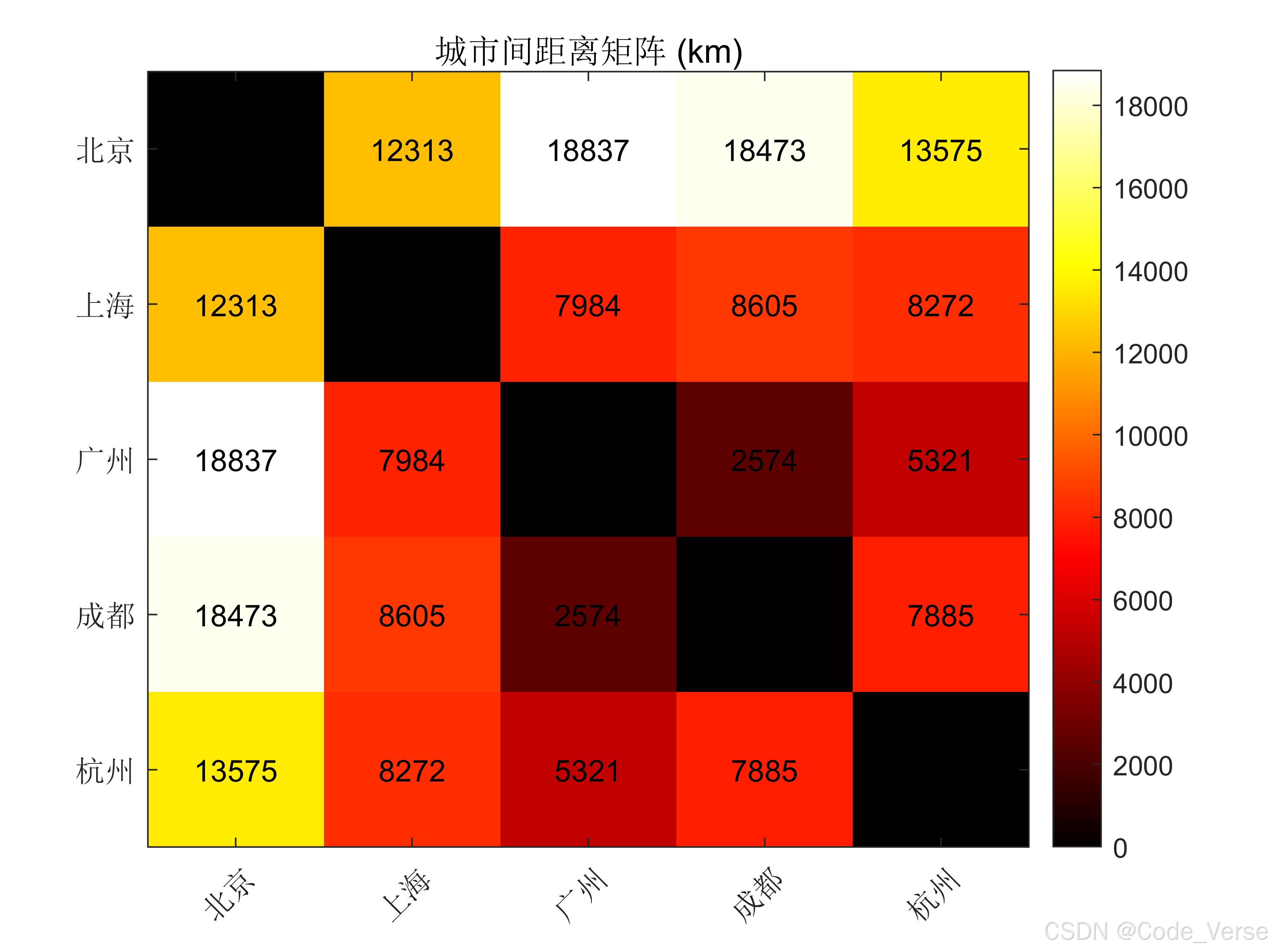

信息分层：热力图提供宏观趋势，数值标签补充精确数据，满足不同分析需求
交互设计：横轴 / 纵轴标签倾斜 45 度，解决中文标签过长导致的重叠问题

四、数据背后的故事：从距离矩阵看城市关联 🌐

1. 距离矩阵解读（部分关键数据）

出发地 \ 目的地	北京	上海	广州	成都	杭州
北京	0	1067	1888	1517	1217
上海	1067	0	1206	1679	177
杭州	1217	177	1113	1851	0

区域邻近性：上海到杭州仅 177km，体现长三角城市群的紧密联系
地理跨度：北京到广州近 1900km，反映南北跨度；成都作为西部中心，到其他城市距离均超 1500km

2. 应用场景拓展

物流规划：根据距离矩阵优化运输路线，降低配送成本
旅游攻略：快速定位邻近城市（如上海 - 杭州周末短途游）
城市研究：分析区域经济圈的空间辐射范围（如长三角、京津冀）

五、技术总结：向量化运算与可视化技巧 🛠️

1. 向量化运算优势

效率：避免for循环，利用 MATLAB 矩阵运算特性，数据量越大优势越明显
简洁：用几行代码实现原本需要嵌套循环的功能，提升代码可读性

2. 可视化最佳实践

兼容性：通过try-catch适应不同环境，确保代码在无专业工具时仍能运行
信息密度：热力图 + 数值标签 + 颜色标尺，多维度呈现数据特征
细节打磨：标签对齐、字体样式、配色方案，提升图表专业性

结语：让地理数据 “说话” 🌟

从经纬度到距离矩阵，从地理分布到热力可视化，这段代码展示了如何用技术手段解锁地理数据的隐藏信息。无论是分析城市关联、优化物流路线，还是制作可视化报告，核心思想始终是：用简洁的代码实现专业的分析，让数据通过可视化 “开口说话”。下次处理地理相关数据时，不妨试试这些技巧，让空间关系一目了然～🌍

互动话题：如果增加更多城市（如西安、武汉），你会如何扩展这段代码？欢迎在评论区分享你的改进思路！👇

完整代码（省流版）

% 生成示例数据（5个中国城市的经纬度：北京、上海、广州、成都、杭州）
vertexs = [
    116.40, 39.90;   % 北京
    121.47, 31.23;   % 上海
    113.26, 23.12;   % 广州
    104.06, 30.67;   % 成都
    120.15, 30.28;   % 杭州
];

% 计算距离矩阵（直接使用用户提供的向量化代码）
lon = vertexs(:,1);
lat = vertexs(:,2);
dlon = lon' - lon;
dlat = lat' - lat;
a = sin(dlat/2).^2 + cos(lat') .* cos(lat) .* sin(dlon/2).^2;
h = 2 * atan2(sqrt(a), sqrt(1-a));
dist = 6378.137 * h;

% 可视化地理分布图
try
    % 如果安装Mapping Toolbox则显示地图背景
    figure;
    geoscatter(lat, lon, 100, 'filled', 'MarkerFaceColor', 'r');
    geobasemap('streets');
    title('城市地理位置分布');
    text(lat, lon, {'北京','上海','广州','成都','杭州'},...
        'VerticalAlignment','bottom', 'FontWeight','bold');
catch
    % 无Mapping Toolbox时使用普通二维图
    figure;
    plot(lon, lat, 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
    xlabel('经度 (°)'); ylabel('纬度 (°)'); title('城市地理位置分布');
    text(lon, lat, {'北京','上海','广州','成都','杭州'},...
        'VerticalAlignment','bottom', 'FontWeight','bold');
    grid on;
end

% 可视化距离矩阵热力图
figure;
imagesc(dist);
colorbar;
title('城市间距离矩阵 (km)');
cities = {'北京', '上海', '广州', '成都', '杭州'};
set(gca, 'XTick',1:5, 'XTickLabel',cities, 'XTickLabelRotation',45);
set(gca, 'YTick',1:5, 'YTickLabel',cities);
colormap hot;

% 在热力图中添加数值标签
for i = 1:5
    for j = 1:5
        text(j, i, sprintf('%.0f', dist(i,j)),...
            'HorizontalAlignment','center');
    end
end