L1和L2及其正则化

大尾巴兔子

已于 2024-11-30 14:41:10 修改

阅读量1.2k

点赞数 20

分类专栏：深度学习文章标签：算法

于 2024-11-30 14:07:28 首次发布

本文链接：https://blog.csdn.net/y330388094/article/details/144150505

版权

深度学习专栏收录该内容

6 篇文章

订阅专栏

1.L1范数（曼哈顿范数）：

表示为从原点到向量所在点的曼哈顿距离。

2.L2范数（欧几里得范数）：

表示为从原点到向量所在点的欧几里得距离。

L1是通过稀疏参数（减少参数的数量）来降低复杂度，L2是通过减小参数值的大小来降低复杂度。

正则化解决过拟合问题

正则化通过降低模型的复杂性，达到避免过拟合的问题。防止模型的过拟合，需要在损失函数LOSS(MSE或者交叉熵)再加上正则项。常用的惩罚项有L1正则项或者L2正则项。

L1、L2的适用场景

由于L1、L2的特点，因此它们也有各自不同的适用场景。

L1：使模型中尽可能多的参数值为0，因此适用于：模型剪枝，模型压缩，特征选择。是一种从改变模型结构的角度（减少模型参数的数量）解决过拟合的方式。

L2：使模型中的所有参数值尽可能小，使得模型尽量不依赖于某几个特殊的特征，而是使每个特征都得到尽量均衡的权重，因此适用于解决普通的过拟合问题，即从参数分布（让分布尽可能的均匀）的角度解决过拟合的问题，这也是常用的解决过拟合的方式。

正则化解释

最基本的正则化方法是在原目标（代价）函数中添加惩罚项（即损失函数），对复杂度高的模型进行“惩罚”。其数学表达形式为：

这里设置J=J0+L，J0为损失函数（目标函数），L为惩罚项损失函数（即L1或者L2）

L1范数：考虑二维的情况，即只有两个权值 w1 和 w2 ，此时 L=|w1|+|w2| 。对于梯度下降法，求解J0的过程可以画出等值线，同时L1正则化的函数L也可以在w1，w2的二维平面上画出来。如下图：

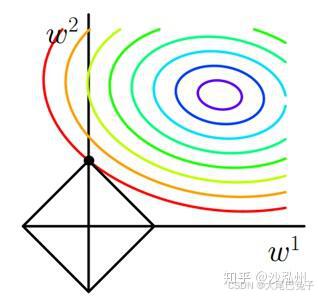
在 L约束下求出 J0 取最小值的解:

根据梯度下降法， J0（椭圆）越靠近圆心，其取值越小；越远离圆心，其取值越大。
同时w1和w2的取值要满足L约束（即最优点要落在 L 菱形图的框上）。
根据上述两个条件可知，当等值线（椭圆）向外扩散时，J0与 L 图形首次相交的地方就是最优解。上图中 J0 与 L 在 L 的一个顶点处相交，这个顶点就是最优解。注意到这个顶点的值是 (w1,w2)=(0,w) 。可以直观想象，因为 L 函数有很多『突出的角』（二维情况下四个，多维情况下更多）， J0 与这些角接触的机率会远大于与 L（菱形）其它部位接触的机率，而在这些角上，会有很多权值等于0，这就是为什么L1正则化可以产生稀疏模型（所谓稀疏权值矩阵指的是很多元素为0，只有少数元素是非零值的矩阵，即得到的线性回归模型的大部分系数都是0）。

在正则化函数前面的系数 α ，可以控制 L 图形的大小。 α 越小， L 的图形越大（上图中的黑色方框）； α越大， L 的图形就越小，可以小到黑色方框只超出原点范围一点点，这时最优点的值 (w1,w2)=(0,w) 中的 w 可以取到很小的值。总而言之，通过调节正则化前面的系数 α，可以控制模型参数取到很小的值，进而防止过拟合。

L2范数：L2正则化不具有稀疏性，同样可以画出他们在二维平面上的图形，如下：

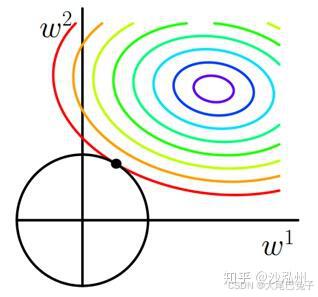
二维平面下L2正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此 J0 与 L 相交时使得 w1 或 w2 等于零的机率小了许多，这就是为什么L2正则化不具有稀疏性的原因。

设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响。专业一点的说法是『抗扰动能力强』。

举个例子，训练集里一共有三男三女6个学生（样本），男生全部红衣服，女生全部绿衣服。现在根据身高、体重和衣服颜色来预测性别。最后在训练集训练出来的结果，衣服颜色这一特征的重要性会非常高，其对应的参数非常大。这就出现了过拟合现象。而一旦拿到测试集中，模型对衣服颜色过分关注的结果必然是预测准确率很低。这种时候，我们对参数的大小是有一定先验的，即通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。

一般认为，参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。

总体来说，L2正则化可以有效的使决策边界更平滑且量级较小，同时也降低了特征之间的依赖度，避免出现过拟合现象，提高了模型的稳定性和泛化能力。 L2正则化可以防止过拟合的原因在于它对模型中的权重进行约束，使权重趋向于较小的值。具体来说，L2正则化在模型优化的过程中，会在损失函数中增加对模型权重平方的正则化惩罚项，使得模型在训练时更加关注权重的大小，并将较大的权重进行惩罚，从而降低了过拟合的风险。通过引入正则化项，L2正则化可以有效控制模型过于复杂，过拟合的情况。同时，L2正则化还可以使模型具有更好的泛化能力，从而适用于更多的数据集。总之，L2正则化通过对权重进行约束，降低模型复杂度，减少过拟合的风险，提高模型的泛化能力。

权重大了可能会导致过拟合的原因有几个方面：

过大的权重会导致模型对于训练数据的细节特征过度拟合，而无法泛化到新的数据上，导致过拟合。
过大的权重也会导致模型的复杂度增加，这会增加模型对于数据的拟合能力，但同时也会降低模型的泛化能力，因为模型可能会学习到训练数据的噪声和不必要的特征。
过大的权重也会导致模型的优化难度加大，因为梯度下降等优化算法可能会因为权重过大而无法收敛。

那为什么L2正则化可以获得值很小的参数？

另一种解释：

C0代表原始的代价函数，后面的那一项是L2正则化项。

正则化项：所有参数w的平方的和，除以训练集的样本大小n。λ就是正则项系数，权衡正则项与C0项的比重。另外还有一个系数1/2，1/2经常会看到，主要是为了后面求导的结果方便，后面那一项求导会产生一个2，与1/2相乘刚好凑整。

我们推导一下看看，先求导：

在不使用L2正则化时，求导结果中w前系数为1，现在w前面系数为 1−ηλ/n ，因为η、λ、n都是正的，所以 1−ηλ/n小于1，它的效果是减小w，这也就是权重衰减（weight decay）的由来。当然考虑到后面的导数项，w最终的值可能增大也可能减小。

另外，需要提一下，对于基于mini-batch的随机梯度下降，w和b更新的公式跟上面给出的有点不同：

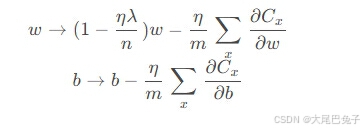
对比上面w的更新公式，可以发现后面那一项变了，变成所有导数加和，乘以η再除以m，m是一个mini-batch中样本的个数。

一个所谓“显而易见”的解释就是：更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合刚刚好（这个法则也叫做奥卡姆剃刀），而在实际应用中，也验证了这一点，L2正则化的效果往往好于未经正则化的效果。

代码测试：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
 
# 生成数据
np.random.seed(10)
X = np.linspace(0, 1, 10)
y = np.sin(2 * np.pi * X) + np.random.normal(0, 0.2, len(X))
X_test = np.linspace(0, 1, 100)
y_test = np.sin(2 * np.pi * X_test) + np.random.normal(0, 0.2, len(X_test))
 
# 不同的模型复杂度
degrees = [1, 3, 10]
X = X[:, np.newaxis]
X_test = X_test[:, np.newaxis]
 
# 绘制结果
plt.figure(figsize=(18, 6))
 
for i in range(len(degrees)):
    
    plt.subplot(1, len(degrees), i+1)
 
    degree = degrees[i]
 
    # 标准多项式拟合
    model = make_pipeline(PolynomialFeatures(degree), Ridge(alpha=0))
    model.fit(X, y)
    y_poly_pred = model.predict(X_test)
    plt.plot(X_test,y_test, color='red', label='True function')
    plt.plot(X_test, y_poly_pred, color='blue', label='Polynomial fit (no L2)')
    plt.scatter(X, y, color='navy', s=40, marker='o', label="training points")
 
    # 将多项式拟合添加L2正则化
    model = make_pipeline(PolynomialFeatures(degree), Ridge(alpha=0.1))
    model.fit(X, y)
    y_poly_pred = model.predict(X_test)
    plt.plot(X_test, y_poly_pred, color='orange', label='Polynomial fit (with L2)')
 
    plt.ylim(-2, 2)
    plt.legend(loc='best')
    plt.title("Degree {}\nTrain Score: {:.3f}, Test Score: {:.3f}".format(
        degree, model.score(X, y), model.score(X_test, y_test)))
 
plt.show()