【8】算法基础：动态规划

最新推荐文章于 2021-02-24 22:55:52 发布

yfraquelle

最新推荐文章于 2021-02-24 22:55:52 发布

阅读量414

点赞数

分类专栏：算法

本文链接：https://blog.csdn.net/y_f_raquelle/article/details/88753969

版权

算法专栏收录该内容

6 篇文章 3 订阅

订阅专栏

如果问题是由交叠的子问题构成的，就可以用动态规划技术来解决它，一般这样的子问题出现在对给定问题求解的递推关系中，这个递推关系中包含了相同类型的更小子问题的解。动态规划法认为与其对交叠的子问题一次又一次地求解，还不如对每个较小的字问题只求解一次并把结果记录下来，这样就可以从记录中得到原始问题的解。

一个经典的使用动态规划思想的问题：斐波那契数列，F(n)是由F(n-1)和F(n-2)两个更小的交叠子问题来得到的，所以，可以在一张一维表中填入n+1个F(n)的连续值，开始时通过初始条件填入0和1，然后根据运算规则计算出其他所有元素。

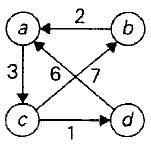
动态规划大多数应用都是求解最优化问题。最优化法则：最优化问题任一实例的最优解都是由其子实例的最优解构成的。最优化法则在大多数情况下是成立的（除了少数情况，如图中的最长简单路径）。

示例1：背包问题

有n个重量为w1,w2,……,wn，价值为v1,v2,……,vn的物品和一个承重W的背包，求这些物品中最有价值的一个子集，且能装到背包中。

假设所有的重量和背包的承重量都是正整数，物品的数量不必是整数。动态规划考虑推导一个递推关系，用较小实例的解的形式来表示背包问题的实例的解。考虑一个由前i个物品定义的实例，物品的重量为w1,w2,……,wi，价值为v1,v2,……,vi，背包承重为j，即求能够放进承重为j的背包中的前i个物品中最有价值子集。将前i个物品中能够放到承重j的背包中的子集分成两类：包括第i个物品的子集和不包括第i个物品的子集。在不包括第i个物品的子集中，最优子集的价值是F(i-1,j)，包括第i个物品的子集(j-wi>=0)中最优子集是由该物品和前i-1个物品中能够放进承重为j-wi的背包的最优子集组成，此时最优子集的总价值等于vi+F(i-1,j-wi)。因此，在前i个物品中最优解的总价值等于这两个价值中的较大者。如果第i个物品不能放入背包，从前i个物品中选出的最优子集的总价值等于从前i-1个物品中选出的最优子集的总价值。

递推式：

F(i,j)=max{F(i-1,j)，F(i-1,j-wi)+vi}（j-wi>=0）

F(i,j)=F(i-1,j)（j-wi<0）

初始条件：j>=0时，F(0,j)=0；i>=0时，F(i,0)=0。

回溯计算过程得到最优子集的组成元素。

def thing_bag(thing_list,W):
    F=[]
    n=len(thing_list)
    for i in range(n+1):
        row=[]
        for w in range(W+1):
            row.append(0)
        F.append(row)
    for t in range(1,n+1):
        for w in range(1, W+1):
            if w-thing_list[t-1][0]>=0:
                F[t][w]=max(F[t-1][w],F[t-1][w-thing_list[t-1][0]]+thing_list[t-1][1])
            else:
                F[t][w]=F[t - 1][w]
    return F
def track_back(F,thing_list,track_stack):
    r,c=track_stack[-1]
    if r>1 and c>1:
        if F[r][c]>F[r-1][c]:
            r_next=r-1
            c_next=c-thing_list[r-1][0]
            track_stack.append([r_next, c_next])
        else:
            track_stack.pop()
            track_stack.append([r-1,c])
        track_back(F,thing_list,track_stack)

def thing_bag_trackback(F,thing_list):
    r=len(F)-1
    c=len(F[0])-1
    track_stack=[]
    track_stack.append([r,c])
    track_back(F,thing_list,track_stack)
    return track_stack
if __name__=="__main__":
    thing_list=[[2, 12], [1, 10], [3, 20], [2, 15]]
    F=thing_bag(thing_list,5)
    for f in F:
        print(f)
    track=thing_bag_trackback(F,thing_list)
    print(track)

示例2：传递闭包

一个有向图的邻接矩阵A={aij}是一个布尔矩阵，当且仅当从第i个顶点到第j个顶点之间有一条有向边时，矩阵第i行第j列的元素为1，如果矩阵表示从i到j是否存在任意长度的有向路径，称为有向图的传递闭包，能够让我们在常数时间内判断第j个顶点是否可从第i个顶点到达。

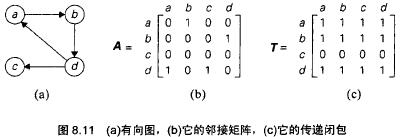
可以在深度优先查找和广度优先查找的帮助下生成有向图的传递闭包，从第i个顶点开始，无论采用哪种遍历方法，都能够得到通过第i个顶点访问到的所有顶点的信息，传递闭包的第i行的相应列置为1。但这个方法对同一个有向图遍历了多次。

Warshall算法通过一系列n阶布尔矩阵来构造传递闭包：

每一个这种矩阵都提供了有向图中有向路径的特定信息，当且仅当从第i个顶点到第j个顶点之间存在一条有向路径（长度大于0），并且路径的每一个中间顶点的编号不大于k时，矩阵Rk的第i行第j列的元素的值等于1。因此，这一系列矩阵从R0开始，这个矩阵不允许它的路径中包含任何中间顶点，所以R0就是有向图的邻接矩阵，R1包含允许使用第一个顶点作为中间顶点的路径信息，推广开来，之后的每一个后继矩阵相对于它的前驱来说，都允许增加一个顶点作为其路径上的顶点，所以可能会包含更多的1。序列中的最后一个矩阵，反映了能够以有向图的所有n个顶点作为中间顶点的路径，因此它就是有向图的传递闭包。

该算法的中心思想是，任何Rk中的所有元素都可以通过它在序列中的直接前驱Rk-1计算得到，把矩阵Rk中第i行第j列的元素rk,ij置为1，这意味着存在一条从第i个顶点vi到第j个顶点vj的路径，路径中每一个中间顶点的编号都不大于k：vi，..每个顶点编号都不大于k的一个中间顶点列表..，vj。

对于这种路径，有两种可能的情况，第一种情况下，路径的中间顶点列表中不包含第k个顶点，那么这条从vi到vj的路径中顶点的编号不会大于k-1，所以rk-1,ij=1。第二种情况是上面这条路径的中间顶点的确包含第k个顶点vk，假设vk在列表中只出现一次（如果出现多次就把头部vk和尾部vk之间的点都去掉），路径就可以改写成这种形式：vi，..编号<=k-1的顶点，vk，编号<=k-1的顶点..，vj。这个表现形式的第一部分意味着存在一条从vk到vk的路径，路径中每个中间顶点的编号都不大于k-1（rk-1,ik=1），第二部分意味着存在一条从vk到vj的路径，路径中每个中间顶点的编号都不大于k-1（rk-1,kj=1）。

以上，如果rk,ij=1，则要么rk-1,ij=1，要么rk-1,ik=1且rk-1,kj=1。易见，它的逆命题也成立，因此：

rk,ij = rk-1,ij或（rk-1,ik和rk-1,kj）。

规则：

如果一个元素rij在Rk-1中是1，它在Rk中仍然是1；如果一个元素rij在Rk-1中是0，当且仅当矩阵中第i行第k列的元素和第k行第j列的元素都是1，该元素在Rk中才能变成1.

import copy

def closure(neigh_mat):
    n=len(neigh_mat)
    R=[neigh_mat]
    for k in range(n):
        R.append(copy.deepcopy(neigh_mat))
    for k in range(1,n+1):
        for i in range(n):
            for j in range(n):
                if R[k-1][i][j]==1 or (R[k-1][i][k-1]==1 and R[k-1][k-1][j]==1):
                    R[k][i][j] = 1
                else:
                    R[k][i][j] = 0
    return R[n]

if __name__=="__main__":
    neigh_mat=[[0,1,0,1,0],
               [0,0,0,0,1],
               [0,0,0,0,0],
               [0,0,1,0,0],
               [0,0,0,0,0]]
    closure=closure(neigh_mat)
    for r in closure:
        print(r)

示例3：完全最短路径

给定一个加权连通图（无向或有向），完全最短路径问题要求找到从每个顶点到其他所有顶点之间的距离。

把最短路径长度记录在一个距离矩阵的n阶矩阵D中，矩阵的第i行第j列的元素dij指出了从第i个顶点到第j个顶点之间的最短路径的长度。

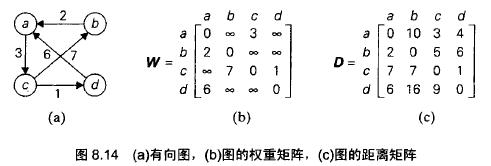
可以使用一种类似于Warshall方法的算法来生成这个距离矩阵，称为Floyd算法。只要图中不包含长度为负的贿赂，这个算法既可以用于无向加权图，也可以用于有向加权图。这个算法通过扩展后不仅可以找到所有顶点对的最短长度，同时还能保存最短路径本身。

Floyd算法通过一系列n阶矩阵来计算一个n顶点加权图的距离矩阵：D0,……,Dk-1,Dk,……Dn，每一个这种矩阵都包含了所讨论的矩阵在特定路径约束下的最短路径长度。Dk的第i行第j列的元素dk,ij等于从第i个顶点到第j个顶点之间所有路径中一条最短路径的长度，并且路径的每一个中间顶点（如果有的话）的编号不大于k。D0不允许路径中包含任何中间顶点，所以D0就是图的权重矩阵，Dn中包含了能够以所有n个顶点作为中间顶点的全部路径中最短路径的长度，所以它就是我们要求的距离矩阵。

和Warshall算法一样，每一个Dk中的任何元素都可以通过它在序列中的直接前驱Dk-1计算得到，把dk,ij作为矩阵Dk中第i行第j列的元素，则dk,ij等于从第i个顶点到第j个顶点之间所有路径中一条最短路径的长度，并且路径的每一个中间顶点的编号不大于k。同样分成两个不相交的子集，中间以顶点vk隔开。所以每条这种路径都由两条路径构成：一条从vi到vk，一条从vk到vj，每个中间顶点的编号都不大于k-1。

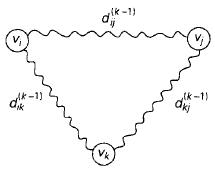
所以得到递推式：dk,ij=min{dk-1,ij，dk-1,ik+dk-1,kj}（k>=1，d0,ij=wij）

另一种表述就是，如果把当前距离矩阵Dk-1中的第i行第j列元素替换为第i行（同一行）第k列元素和第k行第j列（同一列）元素的和，当且仅当后者的和小于它的当前值。

def floyd(distance_mat):
    n=len(distance_mat)
    D=distance_mat
    for k in range(n):
        for i in range(n):
            for j in range(n):
                D[i][j]=min(D[i][j],D[i][k]+D[k][j])
    return D

if __name__=="__main__":
    distance_mat=[[0,float('inf'),3,float('inf')],
                  [2,0,float('inf'),float('inf')],
                  [float('inf'),7,0,1],
                  [6,float('inf'),float('inf'),0]]
    D=floyd(distance_mat)
    for d in D:
        print(d)

示例4：卡塔兰数

卡塔兰数是一种经典的组合数：1，1，2，5，14，42，132，429……

递推式：h(n)=h(0)*h(n-1)+h(1)*h(n-2)+……+h(n-1)h(0)，h(0)=1，h(1)=1

另类递推公式： $h(n)=h(n-1)*\frac{4*n-2}{n+1}$

计算公式： $h_{n}=\frac{1}{n+1} \begin{pmatrix} 2n\\n \end{pmatrix} = \frac{(2n)!}{(n+1)!n!}$

另类计算公式： $hn= \begin{pmatrix} 2n\\n \end{pmatrix} - \begin{pmatrix} 2n\\n-1 \end{pmatrix}$

应用：

n个元素入栈的出栈顺序：先入栈才能出栈，当有n个元素时，我们把问题拆成两个阶段：前k个元素的出入栈和后n-k个元素的出入栈，0<=k<=n，h(n)。

n对括号的组合：先有左括号才能有右括号，h(n)

凸多边形通过互不相交的对角线划分，求划分方案数

圆上选择2n个点，将这些点连接起来，使得所得到的n条线段不相交的方法数

2n边的凸多边形，连接对角线可以分出的三角形的个数

nxn格点中不越过对角线的单调路径的个数

给定n个节点组成二叉搜索树的个数

2n个高矮不同的人站两排，每排从左到右越来越高，有多少种排列方式（由于人不同，需要）

2n个人按顺买票，票价50，其中n个人只有一张50，n个人只有一张100，售票员没有初始零钱，求排队顺利购票的方案数目：有一个50的人买好票才能有一个100的人买，并且带相同面值的人还可以有序：h(n)*n!*n!

https://blog.csdn.net/wu_tongtong/article/details/78161211

https://blog.csdn.net/wookaikaiko/article/details/81105031

https://blog.csdn.net/u010582082/article/details/69569237?locationNum=7&fps=1

def catalan(n):
    H=[1]
    for i in range(1,n):
        sum=0
        for j in range(i):
            sum+=H[j]*H[i-1-j]
        H.append(sum)
    return H
if __name__=="__main__":
    print(catalan(5))

示例5：最优二叉查找树

最优二叉查找树在查找中的平均键值比较次数是最低的。

例如以概率0.1，0.2，0.4，0.3来查找4个键A，B，C，D，包含这些键的二叉查找树有14种不同的可能，下图给出两种情况，左边的平均键值比较次数为0.1x1+0.2x2+0.4x3+0.3x4=2.9，右边是0.1x2+0.2x1+0.4x1+0.3x2=2.1。

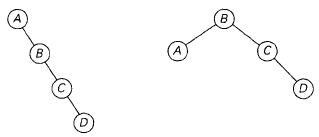
为了找到一种通用的算法，不能使用穷举所有可能的情况。包含n个键的二叉查找树的总数量等于第n个卡塔兰数：

设a1,a2,……,an是从小到大排列的互不相等的键，p1,p2,……,pn是它们的查找概率，Ti,j是ai,……,aj构成的二叉树，C(i,j)是在这棵树中成功查找的最小平均查找次数。虽然只需要C(1,n)，但遵循经典的动态规划方法，求出该问题的所有较小实例的C(i,j)值。对于一棵二叉树，根包含了键ak，则左子树Ti,k-1中的键ai,……,ak-1和右子树Tk+1,j中的键ak+1,……,aj都是最优排列的。

如果从1开始对树的层数进行计算，以使得比较的次数等于键所在的层数，就可以得到下面的递推关系：

递推式：

当1<=i<=n+1时，C(i,i-1)=0，可以解释为空树的比较次数；1<=i<=n时，C(i,i)=pi，是一棵包含ai的单节点二叉树。

动态规划表中的值如下图，他们是i行中位于j列左边的列中的值和j列中在i行下边行中的值，箭头指出需要对元素求和的一对对单元格，求出这些元素对的和的最小值，把它作为C(i,j)的值记录下来，所以我们要沿着表格的对角线填写，目标是右上角。

如果还想得到最优二叉树本身，需要维护另一个二维表来记录达到最小值时的k值。

def fill_c(i,j,p_list,C,K):
    if C[i][j]==-1:
        value_list=[]
        for k in range(i,j+1):
            print(str(i) + "-" + str(j)+" from "+str(i) + "-" + str(k-1)+" and "+str(k+1) + "-" + str(j))
            value_list.append(fill_c(i,k-1,p_list,C,K)+fill_c(k+1,j,p_list,C,K))
        min_value=value_list[0]
        min_k=i
        for x in range(1,len(value_list)):
            if value_list[x]<min_value:
                min_value=value_list[x]
                min_k=i+x
        sum_p=0
        for x in range(i,j+1):
            sum_p+=p_list[x-1]
        C[i][j]=min_value+sum_p
        K[i][j]=min_k
    return C[i][j]
def search_binary_tree(p_list):
    n=len(p_list)
    C=[]
    K=[]
    for i in range(n+2):
        row=[]
        krow=[]
        for r in range(n+1):
            row.append(-1)
            krow.append(-1)
        C.append(row)
        K.append(krow)
    for i in range(1,n+2):
        C[i][i-1]=0
        if i<n+1:
            K[i][i]=i
            C[i][i]=p_list[i-1]
    min_time=fill_c(1,n,p_list,C,K)
    return min_time,C,K
def construct_tree(i,j,start,end,K,path):
    k=K[i][j]
    print(str(k) + " " + str(i) + "-" + str(j))
    if i>=j:
        if i==j:
            path.append(k)
        return
    else:
        path.append(k)
        construct_tree(i,k-1,start,end,K,path)
        construct_tree(k+1,j,start,end,K,path)

if __name__=="__main__":
    p_list=[0.1,0.2,0.4,0.3]
    min_time,C,K=search_binary_tree(p_list)
    print(min_time)
    for c in C:
        print(c)
    print()
    for k in K:
        print(k)
    print()
    path=[]
    construct_tree(1,4,1,4,K,path)
    print(path)

示例6：记忆

直接自顶向下对递推式求解导致一个算法要不止一次地公共的子问题，因此效率是非常低的。经典的动态规划方法是自底向上工作的，它用所有较小子问题的解填充表格，但是每个子问题只解一次。在求解给定问题时，有些较小字问题的解常常不是必须的，由于这个缺点没有在自顶向下法中表现出来，所以我们希望把自顶向下和自底向上方法的优势结合起来，目标是得到一种对必要子问题求解并只解一次，这种方法使用了记忆功能，用自顶向下的方式对给定的问题求解，但还需要维护一个类似自底向上的动态规划算法使用的表格，需要用某个值初始化所有单元格，之后一旦需要计算一个新值，先检查表中相应的单元格，如果不是该值，就从表中取值，否则，递归调用进行计算，然后将返回的结果记录在表中。

仍然是背包问题：

def thing_bag_cell(r,c,thing_list,F):
    if F[r][c]<0:
        if c<thing_list[r-1][0]:
            value=thing_bag_cell(r-1,c,thing_list,F)
        else:
            value=max(thing_bag_cell(r - 1, c, thing_list, F),thing_bag_cell(r - 1, c - thing_list[r-1][0], thing_list, F)+thing_list[r-1][1])
        F[r][c]=value
    return F[r][c]
def thing_bag_memery(thing_list,W):
    F=[]
    n = len(thing_list)
    for i in range(n + 1):
        row = []
        for w in range(W + 1):
            row.append(-1)
        F.append(row)
    for i in range(n+1):
        F[i][0]=0
    for j in range(W+1):
        F[0][j]=0
    thing_bag_cell(n,W,thing_list,F)
    return F
def track_back(F,thing_list,track_stack):
    r,c=track_stack[-1]
    if r>1 and c>1:
        if F[r][c]>F[r-1][c]:
            r_next=r-1
            c_next=c-thing_list[r-1][0]
            track_stack.append([r_next, c_next])
        else:
            track_stack.pop()
            track_stack.append([r-1,c])
        track_back(F,thing_list,track_stack)
def thing_bag_trackback(F,thing_list):
    r=len(F)-1
    c=len(F[0])-1
    track_stack=[]
    track_stack.append([r,c])
    track_back(F,thing_list,track_stack)
    return track_stack

if __name__=="__main__":
    thing_list=[[2, 12], [1, 10], [3, 20], [2, 15]]
    F = thing_bag_memery(thing_list, 5)
    for f in F:
        print(f)
    track=thing_bag_trackback(F,thing_list)
    print(track)

示例7：最长公共子序列LCS

求两个字符串的最长公共子序列，N的长度为n，M的长度为m。F[i,j]表示N的前i个字符与M的前j个字符的最长公共子序列的长度，分为两种情况，如果N的第i个字符和M的第j个字符相等，F[i,j]=F[i-1,j-1]+1，如果不等，F[i,j]=max{F[i-1,j]，F[i,j-1]}，当i或j为0时，F[i,j]=0。

def lcs(l1,l2):
    F=[]
    for i in range(len(l1)+1):
        row=[]
        for j in range(len(l2)+1):
            if i==0 or j==0:
                row.append(0)
            else:
                row.append(-1)
        F.append(row)
    for i in range(1,len(l1)+1):
        for j in range(1,len(l2)+1):
            if l1[i-1]==l2[j-1]:
                F[i][j]=F[i-1][j-1]+1
            else:
                F[i][j] = max(F[i][j-1],F[i-1][j])
    return F,F[-1][-1]
def track_back(F,l1,l2,track_stack,commons):
    i,j=track_stack[-1]
    if i<=0 or j<=0:
        common=[]
        for t in reversed(track_stack[:-1]):
            common.append(l1[t[0]-1])
        commons.append(common)
    else:
        if l1[i-1]==l2[j-1]:
            track_stack.append([i-1,j-1])
            track_back(F,l1,l2,track_stack,commons)
            track_stack.pop()
        else:
            if F[i][j]==F[i-1][j]:
                track_stack.pop()
                track_stack.append([i-1,j])
                track_back(F, l1, l2, track_stack,commons)
            elif F[i][j]==F[i][j-1]:
                track_stack.pop()
                track_stack.append([i, j-1])
                track_back(F, l1, l2, track_stack,commons)

def lcs_trackback(l1,l2,F):
    track_stack=[]
    commons=[]
    i=len(l1)
    j=len(l2)
    track_stack.append([i,j])
    track_back(F,l1,l2,track_stack,commons)
    return commons

if __name__=="__main__":
    l1=['A','D','B','C','D','A','C','B','A']
    l2=['A','B','C','A','D','B','A','C','B']
    F,length=lcs(l1,l2)
    for f in F:
        print(f)
    commons=lcs_trackback(l1,l2,F)
    for c in commons:
        print(c)

示例8：二次项系数

(a+b)^n = C(n,0)*a^n*b^0+ C(n,1)*a^(n-1)*b^1 + … + C(n,k)*a^(n-k)*b^k + … + C(n,n)*a^0*b^n

当n>k>0时nC(n,k) = C(n-1,k-1) + C(n-1,k)，当k=0或k=n时，C(n,0) = C(n,n) = 1

def binary_param(n):
    C=[]
    for i in range(n+1):
        row=[]
        for k  in range(n+1):
            if k==0 or k==i:
                row.append(1)
            else:
                row.append(0)
        C.append(row)

    for i in range(1,n+1):
        for k in range(i+1):
            C[i][k]=C[i-1][k-1]+C[i-1][k]

    return C[-1]
if __name__=="__main__":
    print(binary_param(5))

示例9：最短路径

国际象棋中的车可以水平或竖直移到棋盘中同行或同列的任何一格，将车从棋盘的一角移到另一对角，有多少条最短路径。

只要不走回头路就是最短路径，所以P[i,j]=P[i-1,j]+P[i,j-1]，P[i,0]=1，P[0,j]=1。

def shortest_path(n):
    P=[]
    for r in range(n):
        row=[]
        for c in range(n):
            if r==0 or c==0:
                row.append(1)
            else:
                row.append(0)
        P.append(row)
    for r in range(1,n):
        for c in range(1,n):
            P[r][c]=P[r-1][c]+P[r][c-1]
    return P
if __name__=="__main__":
    P=shortest_path(5)
    for p in P:
        print(p)

yfraquelle

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【8】算法基础：动态规划

如果问题是由交叠的子问题构成的，就可以用动态规划技术来解决它，一般这样的子问题出现在对给定问题求解的递推关系中，这个递推关系中包含了相同类型的更小子问题的解。动态规划法认为与其对交叠的子问题一次又一次地求解，还不如对每个较小的字问题只求解一次并把结果记录下来，这样就可以从记录中得到原始问题的解。一个经典的使用动态规划思想的问题：斐波那契数列，F(n)是由F(n-1)和F(n-2)两个更小的交叠...
复制链接

扫一扫