青蛙一次可以跳上一级台阶,也可以一次跳上两级台阶。那么青蛙跳上n级台阶有多少种方法?
台阶数 方法数
1 1
2 2
3 3
4 5
5 8
· ·
· ·
· ·
由以上数据可以推出从青蛙跳三级台阶开始,f(n) = f(n - 1) + f(n - 2) 这里(n >= 3)(斐波那契数列)
import java.util.Scanner;
public class Test3 {
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();//从键盘输入青蛙要跳的台阶数
int ret = frogjump(n);
System.out.println("青蛙跳" + n + "级台阶,共有" + ret + "种方法");
}
public static int frogjump(int x){
int methonds = 0;
if(x == 1||x == 2)//当台阶数为1和2时,方法数与台阶数相同
methonds = x;
else{//当台阶数大于等于3时,方法数等于前两个台阶数对应的方法数之和
methonds = frogjump(x - 1) + frogjump(x - 2);
}
return methonds;
}
}
测试:
跳一级台阶

跳3级台阶:

青蛙跳45级台阶:
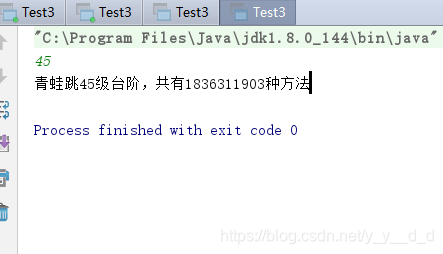
当青蛙跳45级台阶时,方法数已经大约达到18亿种
青蛙跳50级台阶:
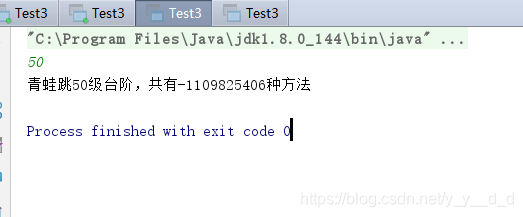
当青蛙跳到50级台阶时,运行时间明显变长,并且结果已经不正确了,这说明int类型的变量已经不够用了
将变量ret,methonds的类型改为double型,将frogjump函数的返回类型也改为double
double ret = frogjump(n);
public static double frogjump(int x)
double methonds = 0;
再次运行青蛙跳
50级台阶的情况,(运行时间依旧很漫长)
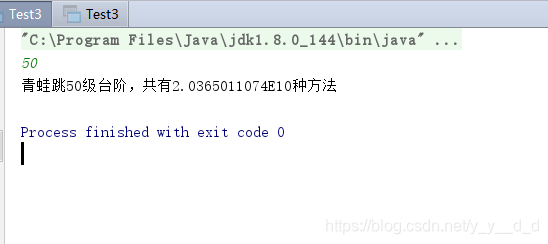







 青蛙跳台阶问题中,从一级到n级台阶有不同的跳跃方式。当n为45时,方法数约达18亿,而跳50级时,使用int类型导致结果错误和运行时间增加。解决方案是将变量类型升级为double。
青蛙跳台阶问题中,从一级到n级台阶有不同的跳跃方式。当n为45时,方法数约达18亿,而跳50级时,使用int类型导致结果错误和运行时间增加。解决方案是将变量类型升级为double。
















 2288
2288

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








