深度学习系统学习系列【5】之深度学习基础（激活函数&损失函数&超参数）-CSDN博客

本文链接：https://blog.csdn.net/yang2330648064/article/details/147722017

不懂机器学习数学原理的算法工程师，并不能称为真正的算法工程师。不懂神经网络数学原理的算法工程师，并不是真正的深度学习拥护者

说明

文章属于个人学习笔记内容，仅供学习和交流。
内容参考深度学习原理与实践》陈仲铭版和个人学习经历和收获而来。

激活函数(Activiation Function)

激活函数实际上隐藏在神经网络模型中的连接线上。

激活函数的一般性质

单调可微：使用梯度下降算法更新神经网络中的参数，因此必须要求激活函数可微。如果函数是单调递增的，求导后函数必大于零（方便计算），因此需要激活函数具有单调性
限制输出值的范围：输入的数据通过神经元上的激活函数来控制输出一个非线性值。通过激活函数求得的数值，根据极限值来判断是否需要激活该神经元。
非线性：激活函数为神经网络模型加入非线性因素。

激活函数的核心意义：一个没有激活函数的神经网络不过是一个线性回归模型，它不能表达复杂的数据分布。神经网络中加入激活函数（引入非线性因素），解决线性模型不能解决的问题。

常见激活函数及优缺点

线性函数

线性（Linear）函数是最基本的激活函数，其因变量与自变量之间有直接的比例关系。因此，线性变换类似于线性回归。
在神经网络中线性变换，意味着节点按原样通过数据信号通常与单层神经网络一起使用。
线性函数的实现：

def liner(x,a,b):
	return a*x+b

在这里插入图片描述

Sigmoid函数

Sigmoid 函数是一种在不删除数据的情况下，减少数据的极值或异常值的函数。未激活值为0，完全饱和的激活值则为1。
Sigmoid 激活函数为每个类输出提供独立的概率。
Sigmoid激活函数具体形式：
$s(x)=\frac{1}{1+e^{-ax}}$
Sigmoid激活函数代码实现

def sigmoid(x,w=1)
	return 1/(1+snp.sum(np.exp(-wx)))

Sigmoid函数图像

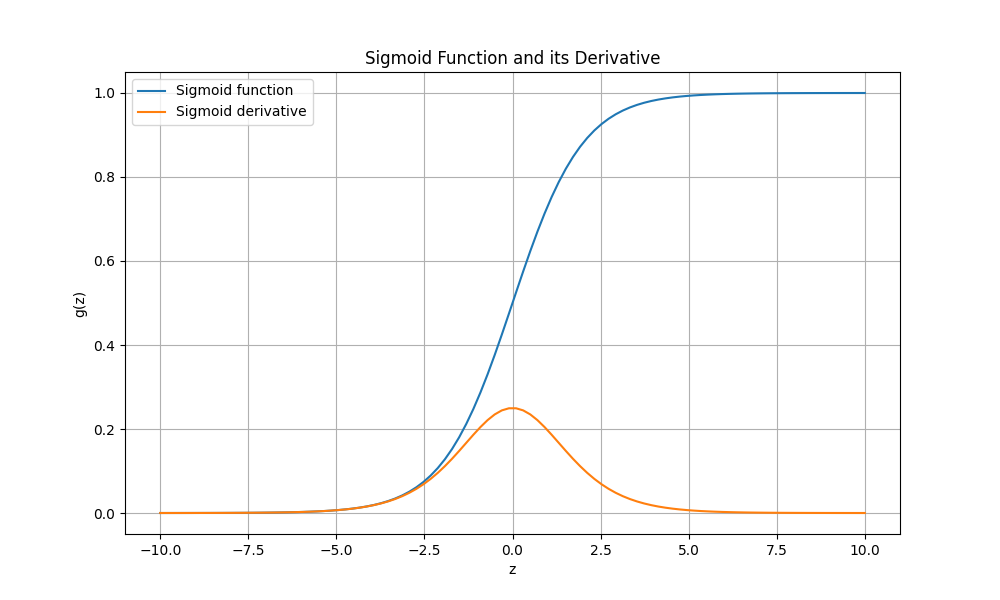
Sigmoid函数优点：
1. 输出映射在［0, 1］范围内，函数单调连续且输出范围有限制，优化稳定。
2. 易于求导，Sigmoid的导数为 $s^{'}(x)=s(x)(1-s(x))$ 。
3. 输出值为独立概率，可以用在输出层。
Sigmoid函数缺点：
- Sigmoid 函数容易饱和，导致训练结果不佳。
- 其输出并不是零均值，数据存在偏差，分布不平均。

Tanh函数

双曲正切函数（Tanh）的归一化范围为[-1,1]，Tanh均值是0，解决了Sigmoid 函数的非 0 均值的缺点。
Tanh 函数会比 Sigmoid 函数更常用。
Tanh函数的公式为：
$tanh(x)=\frac{sinh(x)}{cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
Tanh激活函数代码实现

def tanh(x)
	return np.tanh(x)

Tanh函数图像：
Tanh函数的优点：
1. Tanh 函数比 Sigmoid 函数收敛速度更快，更加易于训练。
2. 其输出以0为中心，数据分布平均。
Tanh函数的缺点：
1. 没有改变Sigmoid 函数由饱和性引起的梯度消失问题。

ReLU函数

研究表明，大脑同时被激活的神经元只有 1% ～ 4%，这表明神经元工作的稀疏性。神经元同时只对输入信号的少部分进
行选择性响应，大量信号被刻意地屏蔽，这样可以提高神经网络的学习精度，更好地提取稀疏特征。

ReLu函数满足仿生学中的稀疏性，只有当输入值高于一定数目时才激活该神经元节点。当输入值低于 0 时进行限制，当输入
上升到某一阈值以上时，函数中的自变量与因变量呈线性关系。
Relu函数的公式表达
$re l u (x) = ma x (0, x)$
ReLu函数的代码实现：

def relu(x)
	return x if x>0 else 0

Relu函数的图像
ReLu函数相较于Sigmoid的变化：

单侧抑制：Sigmoid函数（如 $\frac{1}{1+e^{-x}}$ ）对正负输入均产生平滑响应（输出范围 $(0, 1)$ ），缺乏明确的抑制机制，可能导致梯度在反向传播时因正负输入的混合而减弱。ReLU函数定义为 $\max(0, x)$ ，当输入 $\leq 0$ 时输出恒为0，而 $x > 0$ 时输出线性增长。这种特性使得神经元对负输入完全抑制（“关闭”状态），仅对正输入激活（“兴奋”状态）。
相对宽阔的兴奋边界：Sigmoid函数在 $∣ x ∣$ 较大时进入饱和区（梯度接近0），导致反向传播时梯度指数级衰减（“梯度消失”），尤其对深层网络训练不利。ReLU在 $x > 0$ 时具有线性无饱和的特性（梯度恒为1），允许神经元对大幅正值输入保持强响应，避免了梯度消失问题。这种线性增长的特性使得网络能够更快地适应大范围的数据分布。
稀疏激活性：Sigmoid函数对所有输入均产生非零输出（密集激活），导致神经元间耦合度高，可能引入冗余计算，且不利于特征选择的稀疏性。ReLU的“单侧抑制”特性使得网络中部分神经元在训练过程中输出为0（即“死亡”），仅激活部分神经元。这种稀疏性模拟了生物神经系统的效率，减少了参数间的依赖性，降低了过拟合风险。

ReLu函数的优点：
1. 相比 Sigmoid 函数和 Tanh 函数， ReLU 函数在随机梯度下降算法中能够快速收敛。
2. ReLU 函数的梯度为0或常数，因此可以缓解梯度消散问题。
3. ReLU 函数引入稀疏激活性，在无监督预训练时也能有较好的表现。
ReLu函数的缺点：

ReLU 神经元在训练中不可逆地死亡。某些神经元在训练过程中永久性地停止激活（即输出恒为0），且无法恢复。这种现象被称为“神经元死亡”（Dead ReLU）。
随着训练进行，可能会出现神经元死亡、权重无法更新的现象，流经神经元的梯度从该点开始将永远是零。

Leak Relu函数

Leak ReLu函数是ReLu函数的变体。
- Leaky ReLU：在 $\leq 0$ 时赋予微小斜率（如 $f (x) = 0.01 x$ ），避免梯度消失。
- Parametric ReLU (PReLU)：将负区斜率作为可学习参数。
- Exponential Linear Unit (ELU)：通过指数函数平滑负区，缓解死亡问题。
Leak Relu函数公式：
$\begin{cases} x & \text{if } x > 0\\ kx & \text{if } x \leq 0, k<1 \end{cases}$
Leak ReLu函数的代码实现：

def relu(x,k)
	return x if x>0 else kx

Softmax函数

Softmax 函数的本质是将一个K维的任意实数向量，压缩（映射）成另一个K维的实数向量，其中向量中的每个元素取值都介于（0, 1 ）范围内。
Softmax 是对逻辑回归（Logistic Regression, LR）的推广，逻辑回归用于处理二分类问题，Softmax 回归则用于处理多分类问题。深入内容推荐阅读：从广义线性回归推导出Softmax：理解多分类问题的核心
Softmax函数表达式：
$softmax(x_i)=\frac{e^{x_i}}{\sum_{k=1}^{K}e^{x_k}}$
在数学上，softmax 函数会返回输出类的互斥概率分布。例如，网络的输出为 (1,1,1,1)，经过softmax 函数后输出为(0.25, 0.25, 0.25, 0.25)。
Softmax函数的代码实现

def Softmax(x):
	return np.exp(x)/np.sum(np.exp(x))

Softmax函数通常作为输出层的激活函数。如神经网络有 3 个分类，分别为“野马”，“河马”，“斑马”，使用 Softmax 作为输出层的激活函数。最后只能得到一个最大的分类概率如：野马（0.6）、河马（0.1）、斑马（0.3），其中最大值为野马（0.6）。

激活函数的选择技巧

在选择激活函数时，一般隐层选择LeakReLU 函数。直接使用 ReLU 函数作为激活函数，注意梯度下降算法的学习率参数 $η$ 不能设置得过高，避免神经元的大量 “消亡”。
对输出层，一般使用softmax 函数获得同分布最高概率作为输出结果。

常用损失函数（Loss Function）

在机器学习任务中，大部分监督学习算法都会有一个目标函数 (Objective Function)，算法对该目标函数进行优化，称为优化算法的过程。例如在分类或者回归任务中，使用损失函数（Loss Function）作为其目标函数对算法模型进行优化。
不同的损失函数在梯度下降过程中的收敛速度和性能都是不同的。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 参数设置
plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号

# 生成参数网格
w1 = np.linspace(-4, 4, 100)
w2 = np.linspace(-4, 4, 100)
W1, W2 = np.meshgrid(w1, w2)

# 定义更真实的损失函数
def mse_loss(w1, w2):
    """模拟回归问题的MSE损失"""
    return 0.2*(w1**2 + w2**2) + 0.5*np.sin(w1)*np.cos(w2) + 1

def cross_entropy_loss(w1, w2):
    """模拟分类问题的交叉熵损失"""
    return 2 / (1 + np.exp(-(w1**2 + w2**2)/2)) + 0.3*np.abs(w1-w2)

# 计算损失曲面
MSE = mse_loss(W1, W2)
CE = cross_entropy_loss(W1, W2)
Total = MSE + CE  # 模拟总损失

# 创建三维图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制曲面（调整透明度增强层次感）
surf_mse = ax.plot_surface(W1, W2, MSE, rstride=2, cstride=2, 
                          color='red', alpha=0.7, label='MSE损失')
surf_ce = ax.plot_surface(W1, W2, CE, rstride=2, cstride=2,
                         color='gray', alpha=0.7, label='交叉熵损失')
surf_total = ax.plot_surface(W1, W2, Total, rstride=2, cstride=2,
                            color='blue', alpha=0.5, label='总损失')

# 添加等高线投影（增强立体感）
ax.contour(W1, W2, MSE, zdir='z', offset=0, cmap='Reds')
ax.contour(W1, W2, CE, zdir='z', offset=0, cmap='Greys')

# 设置视角和标签
ax.view_init(elev=30, azim=-45)
ax.set_xlabel(r'$w_1$', fontsize=12)
ax.set_ylabel(r'$w_2$', fontsize=12)
ax.set_zlabel('损失值', fontsize=12)
ax.set_zlim(0, 5)

# 手动创建图例（解决3D图例显示问题）
from matplotlib.patches import Patch
legend_elements = [Patch(facecolor='red', alpha=0.7, label='MSE损失'),
                   Patch(facecolor='gray', alpha=0.7, label='交叉熵损失'),
                   Patch(facecolor='blue', alpha=0.5, label='总损失')]
ax.legend(handles=legend_elements, loc='upper right')

# 添加标题和网格
plt.title('损失函数曲面可视化', pad=20)
ax.grid(True, linestyle=':', alpha=0.5)

plt.tight_layout()
plt.show()

在这里插入图片描述

针对自定义的深度神经网络，深度神经网络中的输出结果包括分类和回归问题，损失函数的模型会变得更加复杂

损失函数的定义

损失函数 $L(Y,\hat y)$ (非负实值函数)，评价预测值 $\hat y=f(X)$ 与真实值 $Y$ 之间的差值。假设网络模型中有 N个样本，样本的输入和输出向量为 $X,Y)=(x_i,y_j),i∈[1,N]$ ，损失函数 $L(Y,\hat Y)$ 是每一个输出预测值与真实值的误差值和。
$L(Y,\hat Y)=\sum_{i=0}^{N}l(y_i,\hat y_i)$

回归损失函数

均方误差损失函数（MSE）

运用均方误差（Mean Squared Error Loss，MSE）的典型回归算法有线性回归（Linear Regression）。
MSE的数学表达：
$loss(Y,\hat Y)=\frac{1}{N} \sum_{i=1}^{N}(\hat y_i-y_i)^2$
MSE的代码实现

def mean_squared_error(y_true,y_pred):
	return np.mean(np.square(y_pred-y_true),axis=-1)

均方误差损失函数的计算公式可以看作欧式距离的计算公式。欧式距离的计算简单方便，而且是一种很好的相似性度量标准，因此通常使用 MSE作为标准的衡量指标。

平均绝对误差损失函数（MAE）

平均绝对误差损失（Mean Absolute Error Loss, MAE），是对数据的绝对误差求平均。
MAE的数学表达：
$loss(Y,\hat Y)=\frac{1}{N} \sum_{i=1}^{N}|\hat y_i -y_i|$
MAE的代码实现：

def mean_absolute_error(y_true,y_pred):
	return np.mean(np.abs(y_pred-y_true),axis=-1)

均方误差对数损失函数（MSLE）

均方误差对数损失(Mean Squared Log Error Loss，MSLE)的数学表达：
$loss(Y,\hat Y)=\frac{1}{N}\sum_{i=1}^{N}(log\hat y_i -log y_i)^2$
MSLE的代码实现：

def mean_squared_logarithmic_error(y_true,y_pred):
	first_log = np.log(np.clip(y_pred, 10e-6, None) + 1.)
	second_log = np.log(np.clip(y_true, 10e-6, None) + 1.)
	return np.mean(np.square(first_log - second_log),axis=-1)

均方误差对数损失函数的实现代码中涉及对数计算，为了避免计算 $l o g 0$ 没有意义，因此加入一个很小的常数 $ε=10^{-6}$ 作为计算补偿。

平均绝对百分比误差损失函数（MAPE）

平均绝对百分比误差损失（Mean Absolute Percentage Error Loss，MAPE）的数学表达：
$loss(Y,\hat Y)=\frac{1}{N} \sum_{i=1}^{N} \frac{100\times |\hat y_i-y_i|}{y_i}$
MAPE的代码实现：

def mean_absolute_percentage_error(y_true, Y_pred):
	diff = np.abs((y_pred - y_true) / np.clip(np.abs(y_true), 10e-6, None))
	return 100 * np.mean(diff,axis=-1)

回归损失函数总结

均方误差函数（MSE）是使用最广泛的损失函数，大部分情况下，均方误差的不错的性能。
MAE 则会比较有效地惩罚异常值，如果数据异常值较多，需要考虑使用平均绝对误差损失作为损失函数。
均方误差对数损失（MSLE）对每个输出数据进行对数计算，目的是缩小函数输出的范围值。
平均绝对百分比误差（MAPE）损失则计算预测值与真实值的相对误差。
均方误差对数损失(MSLE)与平均绝对百分比误差(MAPE)损失实际上是用来处理大范围数据（如 $10^5，10^5]$ ）的。
在神经网络中，常把输入数据归一化到一个合理范围的（如[-1,1])，然后再使用均方误差（MSE）或者平均绝对误差（MAE）损失来计算损失。

神经网络常把输入数据归一化到合理范围方便GPU/CPU进行运算，并提高浮点运算精度，方便观察数据的变化趋势和变化形式。

分类损失函数

Logistic 损失函数

Logistic 损失函数：用于多分类问题，通过最大似然估计使预测概率最大化。
概率定义：
$y_i^{y_i} \times (1 - y_i)^{1 - y_i}$
最大似然函数：
$\text{loss}(Y,\hat{Y}) = \prod_{i=0}^{N} \hat{y}_i^{y_i} \times (1 - \hat{y}_i)^{1 - y_i}$

负对数似然损失函数

为方便数学运算，在处理概率乘积时通常把最大似然函数转化为概率的对数，把最大似然函数中的连乘转化为求和。在前面加一个负号之后，最大化概率 $P (Y ∣ X)$ 等价于寻找最小化的损失。
将概率乘积转化为对数求和形式：

$\text{loss}(Y,\hat{Y}) = -\sum_{i=0}^{N} \left[ y_i \log \hat{y}_i + (1 - y_i)\log(1 - \hat{y}_i) \right]$

交叉熵损失函数

多分类扩展形式（M个类别）：
$\text{loss}(Y,\hat{Y}) = -\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{M} y_{ij} \log \hat{y}_{ij}$

def cross_entropy(y_true, y_pred):
    """交叉熵损失实现"""
    return -np.sum(y_true * np.log(y_pred + 1e-6))

Hinge损失函数

Hinge 损失函数的典型分类器是 SVM 算法，因为Hinge损失可以用来解决间隔最大化问题。当分类模型需要硬分类结果的，例如分类结果是0 或 1、 -1或1的二分类数据， Hinge 损失是最方便的选择。
SVM算法使用的损失函数：
$\text{loss}(Y,\hat{Y}) = \frac{1}{N} \sum_{i=1}^{N} \max(0, 1 - \hat{y}_i \times y_i)$

指数损失函数

典型分类器AdaBoost算法专用：
$\text{loss}(Y,\hat{Y}) = \sum_{i=1}^{N} e^{-y_i \times \hat{y}_i}$

def exponential(y_true, y_pred):
    """指数损失实现"""
    return np.sum(np.exp(-y_true * y_pred))

神经网络中常用的损失函数

自定义损失函数需要考虑输入的数据形式和对损失函数求导的算法。
常见组合：

ReLU + MSE：在神经网络中如果需要使用均方误差损失函数，一般采用 Leak ReLU 等可以减少梯度消失的激活函数。
Sigmoid+ Logistic（交叉熵损失函数）：Sigmoid 函数会引起梯度消失问题，Logistic 损失函数求导时，加上对数后连乘操作转化为求和操作，在一定程度上避免梯度消失。
Softmax + Logistic（交叉熵损失函数）： Softmax 激活函数会返回输出类的互斥概率分布，类 Logisitc 损失函数是基于概率的最大似然估计函数而来的，因此输出概率化能够更加方便优化算法进行求导和计算。

超参数(Hyper Parameters)

在机器学习中，有两种类型参数：一种是与网络模型相关的参数，另一种是与网络模型调优训练相关的参数。与模型调优训练有关的参数目的是让模型训练的效果更好、收敛速度更快，而这些调优参数被称为超参数（HyperParameters）。
超参数选择需要保证神经网络模型在训练、阶段既不会拟合失败，不会过度拟合，同时让网络尽可能快地学习数据结构特征。

学习率（Leaming Rate）

梯度下降算法： $\theta \leftarrow \theta -\eta \frac{\partial L}{\partial \theta}$
$\eta$ 为学习率， $\theta$ 为网络模型参数， $L(\theta)$ 为损失函数。
网络参数 $\theta$ 的更新依赖于梯度误差与学习率：在神经网络的训练阶段，调整梯度下降算法的学习率可以改变网络权重参数的
更新幅度。学习率越大，参数θ的更新步长越大：学习率越小，参数θ的更新步长越小。
为使梯度下降法具有更好的性能，需要把学习率的值设定在合适的范围内，因为学习率决定参数能否移动到最优值和参数移动到最优值的速度。
学习率影响算法性能表现，好的学习率，对应的误差曲线应该具有很好的平滑性，并且最终使得网络达到最优的性能。一般情况下，高学
习率使得误差下降得很快，低学习率可以使得误差下降平滑。
在网络训练初期使用高学习率，当误差降低幅度减少时转而采用较低的学习率，让误差继续平滑下降，让模型训练得到更好的效果。例如将学习率的初始值设为 0.1，若在验证集上误差性能不再提高，可以将学习率除以2或者5，如此循环，直到算法收敛。

动量（Momentum）

动量（Momentum）是梯度下降优化算法的改进技术，通过引入历史梯度信息来加速收敛并减少震荡。
当梯度保持相同方向维度时，动量不断增大，梯度方向在不停变化的维度上，动量持续减少。因此可以加快收敛速度并减
少震荡。网络中的参数通过动量来更新，参数向量会在任何有持续梯度的方向上增加速度。
$v_t = \gamma v_{t-1} + \eta \nabla_\theta J(\theta) \\ \theta_{t+1} = \theta_t - v_t$
$v_t$ ：当前时刻的动量向量
$\gamma$ ：动量系数（通常设为0.9）
$\eta$ ：学习率
$\nabla_\theta J(\theta)$ ：参数θ的梯度

动量法的物理类比：

类似小球滚下山坡时积累动量
在梯度方向一致的维度上加速更新
在梯度方向变化的维度上抑制震荡

class MomentumOptimizer:
    def __init__(self, lr=0.01, gamma=0.9):
        self.lr = lr
        self.gamma = gamma
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = np.zeros_like(params)
        
        self.v = self.gamma * self.v + self.lr * grads
        return params - self.v