多阶段决策过程的最优化问题（动态规划）

多阶段决策过程，是指这样的一类特殊的活动过程，问题可以按时间顺序分解成若干相互联系的阶段，在每一个阶段都要做出决策，全部过程的决策是一个决策序列。

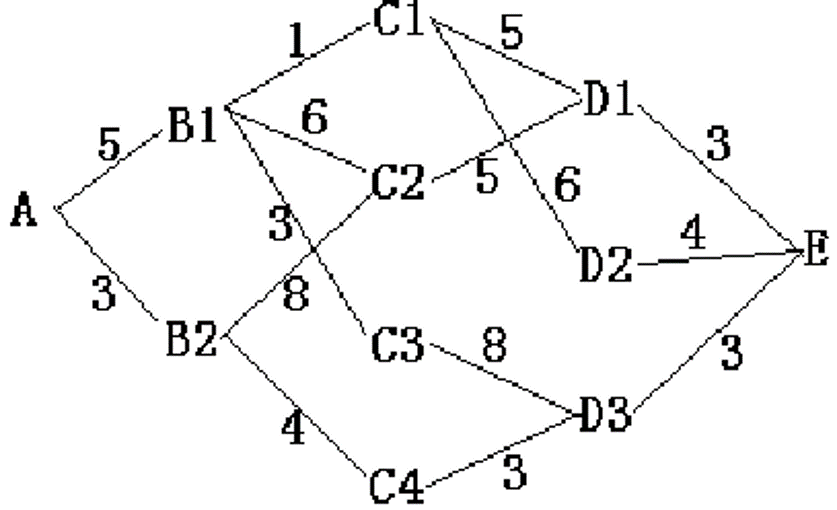
【例题】最短路径问题。下图给出了一个地图，地图中的每个顶点代表一个城市，两个城市间的一条连线代表道路，连线上的数值代表道路的长度。现在想从城市A到达城市E，怎样走路程最短？最短路程的长度是多少？

#include<iostream>
#include<cstring>
using namespace std;
int f[6][6];//f[i][j]表示第i个阶段第j个数的最短路径
int a[6][6][6];//a[i][j][k]表示第i个阶段第j个数到下一阶段第k个数的路径长度 
int main()
{
	memset(a,0x3f,sizeof(a));//求最小值时一定要记得初始化为最大值 
    memset(f,0x3f,sizeof(f));
	a[1][1][1]=5;a[1][1][2]=3;
	a[2][1][1]=1;a[2][1][2]=6;a[2][1][3]=3;
	a[2][2][2]=8;a[2][2][4]=4;
	a[3][1][1]=5;a[3][1][2]=6;
	a[3][2][1]=5;
	a[3][3][3]=8;
	a[3][4][3]=3;
	a[4][1][1]=3;a[4][2][1]=4;a[4][3][1]=3;
	f[5][1]=0;
	for(int i=4;i>=1;i--)
	{
		for(int j=1;j<=4;j++)
		{
			for(int k=1;k<=4;k++)
			{
				if(f[i][j]>a[i][j][k]+f[i+1][k]) 
			    {
			    	f[i][j]=a[i][j][k]+f[i+1][k];
			    }
			}
		}
	}
	 
	cout<<f[1][1]<<endl;
	return 0;
} 

输出答案：13