二分查找万能模板（基础版）

IncludeFun

已于 2023-02-19 18:28:19 修改

阅读量825

点赞数 4

分类专栏：算法文章标签：算法数据结构 c++ 剪枝

于 2023-02-19 16:45:10 首次发布

本文链接：https://blog.csdn.net/yaoyaoxuanxuan1/article/details/129110080

版权

算法专栏收录该内容

5 篇文章 0 订阅

订阅专栏

1.前言

二分思想并不难理解，但是其难点在于根据题目的实际要求设计算法的过程中的细节把握，包括但不限于：

区间类型怎么取（左闭右闭？左开右闭？or其他？）
循环条件怎么写（l<=r还是l<r甚至l+1<r）
剪枝语句的条件和执行体如何设计
对于不同的题目模板应采用怎样的设计（序列是严格单调还是非严格单调？所求为满足条件的位置还是“第一个”满足条件的位置抑或“最后一个”满足条件的位置）

每当这些需要考虑的因素综合在一起，就变成了一场大脑的灾难。因此这篇文章希望通过对二分进行高度的归纳和概括，并在文章最后给出一种解决二分问题的万能模板

2.两种经典模型

严格单调序列中查找值x的位置

题目：小明从[A,B]区间中随机想一个数字，小红需要猜出他想的是什么数字，每猜一次小明都会告诉她她猜的数字比自己想的数字大还是小还是正好相等，设计一个让小红猜最少次数的算法
代码：

//在[A,B]区间内查找x的位置，若不存在则返回-1
int search(int A,int B,int x)
{
	while(A<=B)
	{
        //取中间位置为本轮的猜测值
        int mid = (A+B)/2;
        if(mid==x) {
            return mid;
        }
        else if(mid<x){
            A=mid+1;
        }else{
            B=mid-1;
        }
	}
    return -1;
}

代码很简单，但是里面蕴含着二分的关键基础，我将其命名为“单行道性”，即每轮迭代中，三个条件语句if,else if和else只能进入其中一个，其他的都是不可能的答案区间
下图是二叉树的搜索过程示例，如当前搜索的是2号结点，虽然3号结点还未搜索，但是3号结点及其子树中依然可能存在可行解
在这里插入图片描述

而下图是二分的查找过程示意图，可以看到一旦进入2号区间搜索，那么3号区间就一定不可能有解
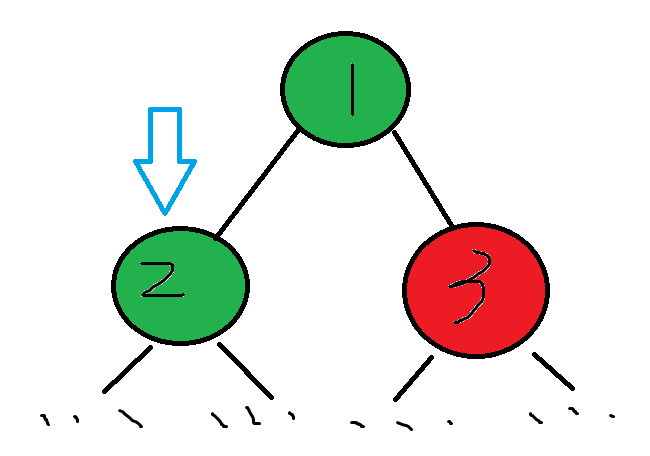
在这里插入图片描述
这种特性的基础是二分序列的有序性，这种特性的好处是高效的剪枝效率，由此可以导出一个重要的中间结论：一旦搜索进入到最后的叶子区间也即[l,r]（l==r）的并且不管是因为何种原因退出的时候，整个算法就一定结束了，根本不存在这个叶子区间爆了，然后还需要再换另一侧区间或者其他某个合理区间再查找的情况。用一句话概括：当前搜索的这个区间一定是唯一的可能和希望，如果它都不行那其他区间一定也不行,整个求解路径是一条单行道，没有后退可言也没有后退的必要。理解了这一点，就可以更好地理解后面提到的种种纷繁复杂的情况下当退出while循环的时候究竟意味着什么。

非严格单调序列中第一个大于等于x的位置

题目：查找非递减序列中第一个大于等于x的元素的位置
代码：

int lower_bound(int l,int r,int x)
{
    int mid;//mid为l和r的中点
    int answer = -1;
    while(l<=r)
    {
        mid=(l+r)/2;
        if(A[mid]>=x){//中间的数大于等于x
            answer = mid;
            r = mid;//往左子区间[l,mid]中继续找
        }else{
            l = mid + 1;//往右子区间[mid+1,r]中找
        }
        if(l==r)break;
    }
    return answer;//返回夹出来的位置
}

这个模型本身并不难理解，和前面查找x位置的模型的区别有三条：

1.满足条件时的处理方式不同

在查找x位置的模型（后称模型1）中，一旦发现满足条件的位置就要立即返回，因为任务已经完成；但是在查找第一个大于等于x的位置的模型（后称模型2）中，发现满足条件的位置后（A[mid]>=x）并没有返回而是在包含当前值的左区间内继续查找，这是一种骑驴找马的思想，即已经有了mid是满足的，但是还想要第一个满足的，于是想往前再试试，但是试的过程中又不能丢了当前已经发现的解，万一前面没有了呢，于是这里并非模型1的r=mid-1而是r=mid，在下一次搜索中把已知解mid也包含了进去，下一次搜索如果找到新的更靠左更让我们满意的可行解，就对其也进行相同的处理（进入保留其值的左区间搜索），要是下一次搜索没有找到新的更好的解，那么就进入右区间，这样本轮的解依然被沉淀在了搜索区间的最右侧，由此我们可以得到另外一条重要的信息：在搜索过程中一旦遇到一次可行解，那么在之后的任何一次迭代中，搜索空间的右端点都是当前最优最靠左的可行解，这条结论后面会用到

2.退出迭代的条件不同

在模型1的论述中我们说过，退出迭代意味着所有的可能都已经考虑完毕，模型1属于见好就收，而模型2则需要不撞南墙不回头，但是在试探的过程中使用answer记录了最后一个也是最优的可行解，也即“序列中第一个大于等于x的位置”，退出迭代后将其返回即可，若answer=-1表示序列中没有这样的位置，说明在搜索中一次都没有找到满足条件的mid就退出的迭代

3.新增if(l==r)break;语句

由于将r=mid-1改为了r=mid，因此搜索区间在收敛到l==r时如果满足条件则会进入死循环，因此需要补充判断退出语句

3.由两种经典模型外推

在单调非减序列中求解第一个大于等于x的位置问题中，有时又将它写成这样

int lower_bound(int l,int r,int x)
{
    int mid;//mid为l和r的中点
    while(l<r)
    {
        mid=(l+r)/2;
        if(A[mid]>=x){//中间的数大于等于x
            r = mid;//往左子区间[l,mid]中继续找
        }else{
            l = mid + 1;//往右子区间[mid+1,r]中找
        }
    }
    return l;//返回夹出来的位置
}

区别在于，去除了answer变量，最终返回值为区间左端点l，并且将迭代条件替换为了l<r，在初学的时候我也将其看作是[l,r)左闭右开区间的意思（当然这么认为也没问题，只是解读视角不同而已），虽然脑海中能演练出这个算法的流程和合理性，但是却因为无法与l<=r的模型联系起来而没有融汇贯通，这里我继续采用[l,r]左闭右闭区间的视角来解读这段代码：
之前提到：在搜索过程中一旦遇到一次可行解，那么在之后的任何一次迭代中，搜索空间的右端点都是当前最优最靠左的可行解，当进入[l,r],l==r区间时，只有两种可能：要么l就是沉淀下来的那个最优解，要么整个A数组中根本不存在这样的位置。照l<=r判断的逻辑来说，这里应该这么判断，要是是最优解就输出，要不是退出返回-1，这样当然没有问题。有趣的是，我们得到过结论：当前搜索的区间一定是唯一可能的区间，也即现在只剩l（或r）一个可能的点了，如果这时候还不满足则说明假设x在序列中，那么它一定应该正好排在这个位置（可惜不在），因此我们没有必要再对l=r进行处理，将迭代循环条件退化为l<r，这时候最终输出的l是假设x存在的话应该在的位置。
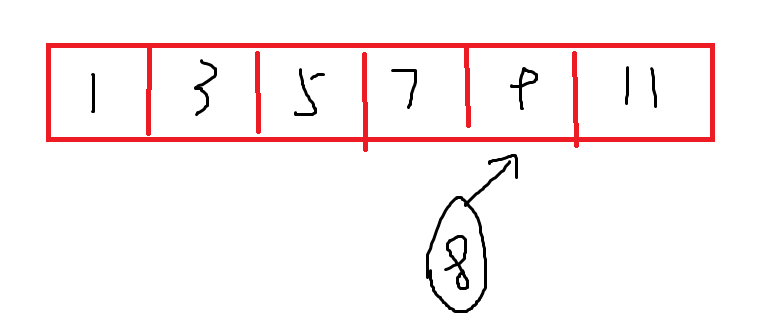
在这里插入图片描述
**如上图，8本应存在的位置正好就是第一个大于等于8的数的位置。**但这依然不完全解决问题，假如我们要搜索的时第一个大于等于15的位置

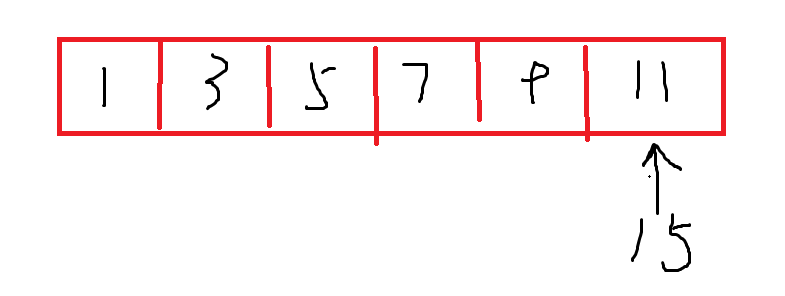
程序会在这里停止迭代并退出，该位置是显然不是第一个大于等于15的位置。处理这种情况的方法是：将起始边界扩展一个单位，比如我们一开始要搜索的区间是A[0]-A[N]，即调用lower_bound(0,N,x)，但是我们故意将起始搜索区间置为A[0]-A[N+1]，即调用lower_bound(0,N+1,x)，这样当退出迭代时的l=N+1时就说明它应该在这个原序列中根本不存在的位置，换言之：原序列中没有大于等于它的数
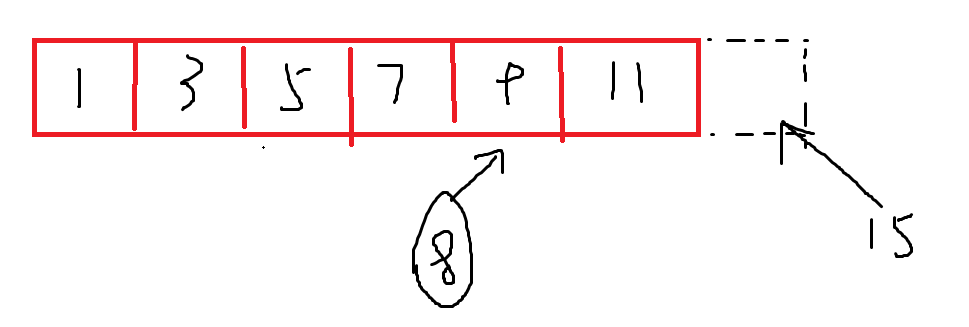
在这里插入图片描述
这里使用[0,N+1]区间来搜索[0,N]区间的问题和迭代条件l<r搭配则提供了从另一个角度解读算法的空间，即将所有搜索区间视为左闭右开区间，但这只是解读视角的问题，同时也对理解造成了干扰，因此本文从始至终始终采用统一的原则即左闭右闭区间的视角来解读所有二分问题。

总结

这节我们得到了一个非常有用的结论：while()语句中的条件，调用时是否扩展一个单位的边界以及返回l还是返回维护的answer值是三位一体，相互配合的，下面做出总结：

1.while(l<=r) 配合 return 直观答案

思想：一是一，二是二，无的说不成有，有的说不成无，退出迭代时，l和r的值不再使用，因为就是因为l和r交错开才导致的退出迭代，因此其值或许可以看作混乱没有意义，返回值需要另外维护（如模型1中一旦发现就返回mid，否则返回-1，以及模型2中手动维护answer值）

使用方法：传参时不扩展原有边界

2.while(l<r) 配合 return l（或return r）

思想：旁敲侧击，间接论证，退出迭代时一定为l==r的情况，这种“夹起来”的区间或点有直接意义，即“假设x存在的话应该在这里”，可以间接转换为题目需要的“第一个XXXX的位置”

使用方法：传参时扩展一个单位的原有边界

4.二分查找万能模板

在前言中提到，二分查找问题存在如下这些让人头疼的变量

区间类型怎么取（左闭右闭？左开右闭？or其他？）
循环条件怎么写（l<=r还是l<r甚至l+1<r）
剪枝语句的条件和执行体如何设计
对于不同的题目模板应采用怎样的设计（序列是严格单调还是非严格单调？所求为满足条件的位置还是“第一个”满足条件的位置抑或“最后一个”满足条件的位置）

而在之前的论述中，已经解决的问题有：区间类型的选取和循环条件的写法。其中区间类型可以选择任何类型，只要解读问题的视角正确，这个不是影响二分的关键，使用左闭右开区间能解决的问题，使用左闭右闭，甚至左开右开思路一样能解决，只需要设计配套的流程即可，本文全称使用左闭右闭视角，所得结论也全部基于此前提下；循环条件的选择也在上个小节进行了论述。
因此剩下的问题有两个：1.剪枝语句的条件和执行体的设计 2.不同的题目类型。下面的万能模板由题目类型搭起基本框架，再由题目具体要求完善剪枝设计：

1.在A序列（0~n-1）中查找满足条件B的位置

A=单调递增，单调递减，单调非增，单调非减
B=等于x，大于x，小于x，大于等于x，小于等于x……

int main()
{
	int res = search(0,n-1,x);//不外扩边界
}
int search(int left,int right,int x)
{
	while(left<=right)
	{
        //取中间位置为本轮的猜测值
        int mid = (left+right)/2;
        if(满足条件B) {
            return mid;
        }
        else if(不满足条件B但可以由
        	1.理想：希望满足的x和mid间的条件B
            2.现实：x和mid之间实际存在的关系
            3.序列的有序关系A
            三个信息简单推得解只可能在mid的右边){
            left=mid+1;
        }else{
            right=mid-1;
        }
	}
    return -1;
}

2.在A序列中查找第B个满足C条件的位置

A=单调递增，单调递减，单调非增，单调非减
B=第一个，最后一个
C=等于x，大于x，小于x，大于等于x，小于等于x……

int main()
{
	int res = search(-1或0,n-1或n,x);//根据需要外扩边界
}
int search(int l,int r,int x)
{
    int mid;//mid为l和r的中点
    while(l<r)
    {
        mid=(l+r)/2;
        mid=(l+r)/2+1;//若需要找最后一个，需要调整这里，否则会死循环
        if(满足条件B){
            要么 r = mid;//若需要找第一个，则往左子区间[l,mid]中继续找
            要么 l = mid;//若需要找最后一个，则往右子区间[mid,r]中继续找
        }else if(不满足条件B但可以由
        	1.理想：希望满足的x和mid间的条件B
            2.现实：x和mid之间实际存在的关系
            3.序列的有序关系A
            三个信息简单推得解只可能在mid的右边){
            left=mid+1;
        }else{
            right=mid-1;
        }
    }
    return l;//返回夹出来的位置
}

总结

int main()
{
	int res = search(0,n-1,x);//问题模型1
	int res = search(-1或0,n-1或n,x);//问题模型2
}
int search(int l,int r,int x)
{
    int mid;
    while(l<=r)//问题模型1
    while(left<r)//问题模型2
    {
        mid=(l+r)/2;//问题模型1和问题模型2之找第一个xxx
        mid=(l+r)/2+1;//问题模型2之找最后一个xxx
        if(满足条件B){
            return mid;//问题模型1
            r = mid;//问题模型2之找第一个xxx
            l = mid;//问题模型2之找最后一个xxx
        }else if(不满足条件B但可以由
        	1.理想：希望满足的x和mid间的条件B
            2.现实：x和mid之间实际存在的关系
            3.序列的有序关系A
            三个信息简单推得解只可能在mid的右边){
            left=mid+1;
        }else{
            right=mid-1;
        }
    }
    return-1;//问题模型1
    return l;//问题模型2
}