数据结构（Java）--排序

排序的基本概念

• • （1）排序的数据序列与关键字
  • • n数据序列指待排序的数据元素集合，排序是以关键字为基准进行的，
      n排序过程指将一个数据序列中的元素按照关键字值大小递增（或递减）的次序重新排列。
      n升序（正序）：按关键字从小到大排列得到的序列。
      n降序（反序） ：按关键字从大到小排列得到的序列。

（2）

排序算法的性能评价

（a）评价排序算法好坏的标准：

     ① 执行时间和所需的辅助空间

     ② 算法本身的复杂程度

（b）排序算法的空间复杂度

     Ø若排序算法所需的辅助空间并不依赖于问题的规模n，即辅助空间是O(1)，则称之为就地排序。

     Ø非就地排序一般要求的辅助空间为O(n)。

（c）

排序算法的时间开销

     大多数排序算法的时间开销主要是关键字之间的比较和记录的移动。有的排序算法其执行时间不仅依赖于问题的规模，还取决于数据序列中数据的初始状态（升序、降序、随机顺序？）。

（d）排序算法的基本操作

     （a）比较两个关键字大小（比较）

                    keys[i]    ?    keys[j]

     （b）将记录从一个位置挪到另一个位置（移动、交换）

      private static void swap(int[] keys, int i, int j)   

 //交换keys[i]与keys[j]元素，i、j范围由调用者控制

 {
        int temp = keys[j];
        keys[j] = keys[i];
        keys[i] = temp;
    }

• 
  

（3）排序算法的稳定性（相同元素排序之后的顺序）

l当按照数据序列的主关键字进行排序时，排序结果是唯一的，否则排序结果不唯一。

在数据序列中，若存在多个关键字相同的记录，经过排序后这些具有相同关键字的记录之间的相对次序保持不变，该排序方法是稳定的。

  l 若具有相同关键字的记录之间的相对次序发生变化，则称这种排序方法是不稳定的。

（4）内排序与外排序（与内存有关）

n在排序过程中，若整个数据序列都是放在内存中处理，即排序时不涉及数据的内、外存交换，则称之为内部排序(简称内排序)；

n

反之，若排序过程中要进行数据的内、外存交换，则称之为外部排序

(简称外排序)

。

注意：
① 内排序适用于记录个数不很多的小文件
② 外排序则适用于记录个数太多，不能一次将 

   其全部记录放入内存的大文件。

按排序所采用的策略对内排序分类

插入排序：直接插入排序、二分法  插入排序、希尔排序

交换排序：冒泡排序、快速排序

选择排序：直接选择排序、堆排序

归并排序

     基数排序

  1  插入排序

• 插入排序的基本思想是：每趟将一个元素，按其关键字大小，插入到它前面已排序的子序列中，使得插入后的子序列仍是排序的，依次重复直到全部元素插入完毕。
• • • • 1.1  直接插入排序和二分法插入排序
      • • 1、直接插入排序
        • • 
            
        • 2、直接插入排序算法分析

        • • (1)算法的时间性能分析

            对于具有n个记录的数据序列，要进行n-1趟排序。
          • • 
              

          • (2)算法的空间复杂度分析

              算法所需的辅助空间是一个临时变量temp，辅助空间复杂度S(n)=O(1)。是一个就地排序。

            (3)直接插入排序的稳定性

              直接插入排序是稳定的排序方法。
      • 3、二分法插入排序

        直接插入排序是采用顺序查找寻找插入位置。

        二分法插入排序是采用二分法查找寻找插入位置。
      • • 
          
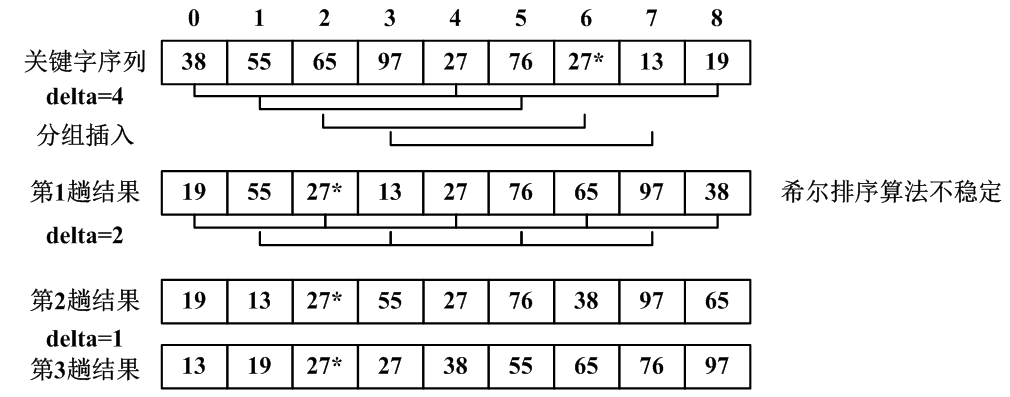
      • 1.2   希尔排序（shell sort）
      • • 希尔排序又称缩小增量排序。
        • 实质是分组的直接插入排序。
        • 改进的依据是：
      1. 1. 若数据序列接近有序，则时间效率越高；
         2. 当n较小时，时间效率也较高。
      • 1、希尔排序算法
      • • 
          
      • 2、希尔排序算法分析

  2   交换排序

• • • • 交换排序的基本思想是：两两比较数据序列中的关键字，发现两个记录的次序相反时即进行交换，直到没有反序的记录为止。

•  1   冒泡排序
• • 
    
  • • 交换排序的基本思想是：两两比较数据序列中的关键字，发现两个记录的次序相反时即进行交换，直到没有反序的记录为止。

• • 1   冒泡排序
    1、冒泡排序算法
  • • • • 
          

                               2、冒泡排序算法分析

（1）算法的最好时间复杂度

若初始数据序列的初始状态是升序的，一趟扫描即可完成排序。所需的关键字比较次数C和记录移动次数M均达到最小值：

        Cmin=n-1

        Mmin=0。

冒泡排序最好的时间复杂度为O(n)。

（2）算法的最坏时间复杂度

若初始数据序列的初始状态是降序的，需要进行n-1趟排序。每趟排序要进行n-i次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录3次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值：
        Cmax=n(n-1)/2=O(n2)
        Mmax=3n(n-1)/2=O(n2)

冒泡排序的最坏时间复杂度为O(n2)。

• （3）算法的平均时间复杂度为O(n2)

     数据序列的初始排列越接近升序，冒泡排序效率越高。

       虽然冒泡排序不一定要进行n-1趟，但由于它的记录移动次数较多，     故平均时间性能比直接插入排序要差得多。

（4）算法稳定性

     冒泡排序是就地排序，且它是稳定的。

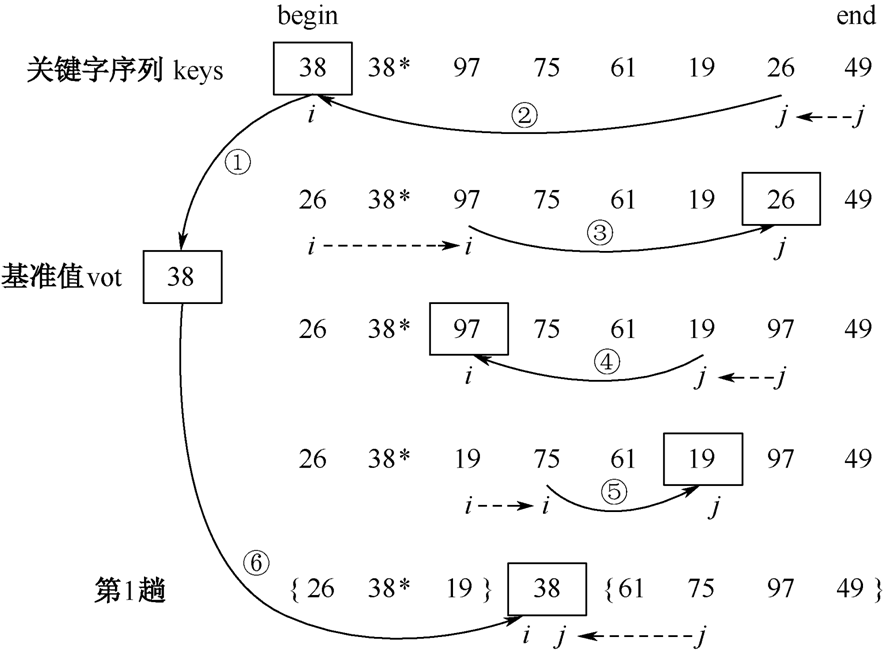
• • 2   快速排序（原顺序越乱越好）
    1、快速排序算法
    n快速排序是一种分区交换排序算法。
    n快速排序算法尽可能地减少重复的数据移动。
    n当n较大且数据序列随机排列时，快速排序是“快速”的。
  • • • • 
          
        • 快速排序过程
        • • • • • • 
                    
    • 2、快速排序算法分析
    • • • • n快速排序的时间主要耗费在划分操作上，对长度为k的子序列进行划分，共需k-1次关键字的比较。

            （1）最坏时间复杂度
               　最坏情况是每次划分选取的基准都是当前排序子序列中关键字最小(或最大)的记录，划分的结果是基准左边的子序列为空(或右边的子序列为空)，而划分所得的另一个非空的子序列中记录数目，仅仅比划分前的排序子序列中记录个数减少一个。
                　因此，快速排序必须做n-1次划分，第i次划分开始时子序列长度为n-i+1，所需的比较次数为n-i(1≤i≤n-1)，故总的比较次数达到最大值：
                           Cmax= n(n-1)/2=O(n2)
                　如果按上面给出的划分算法，每次取当前数据序列的第1个记录为基准，那么当记录已呈升序(或降序)排列时，每次划分所取的基准就是当前数据序列中关键字最小(或最大)的记录，则快速排序所需的比较次数反而最多。

          • （2） 最好时间复杂度

            在最好情况下，每次划分所取的基准都是当前子序列的“中值”记录，划分的结果使得基准的左、右两个子序列的长度大致相等。总的关键字比较次数： O(nlog2n)。
            因为快速排序的记录移动次数不大于比较的次数，所以快速排序的最坏时间复杂度应为O(n2)，最好时间复杂度为O(nlog2n)。

            （3）平均时间复杂度
            尽管快速排序的最坏时间为O(n2)，但就平均性能而言，它是基于关键字比较的内部排序算法中速度最快者，快速排序亦因此而得名。它的平均时间复杂度为O(nlog2n) 。

（4）空间复杂度

    　快速排序在系统内部需要一个栈来实现递  归。若每次划分较为均匀，则其递归树的  高度为O(log2n)，故需栈空间为  O(log2n) 。最坏情况下，递归树的高度  为O(n)，所需的栈空间为O(n)。

（5）稳定性

    　快速排序是非稳定的。

• • • • • • • 3   选择排序 
            • • • 选择排序(Selection Sort)的基本思想是：每一趟从待排序的记录中选出关键字最小的记录，顺序放在已排好序的子文件的最后，直到全部记录排序完毕。

                                1  直接选择排序（需要一个元素来存待交换元素的值）

• • • • • • • 1、直接选择排序算法
            • • 
                

2、直接选择排序算法分析

（1）关键字比较次数

无论数据序列的初始状态如何，在第i趟排序中选出最小关键字的记录，需做n-i次比较，因此，总的比较次数为：

（2）记录的移动次数

  当数据序列的初始状态为升序时，移动次数为0当数据序列的初始状态为降序时，每趟排序均要执行1次交换操作，总的移动次数取最大值3(n-1)。

直接选择排序的平均时间复杂度为O(n2)。

• • • • • • • （3）直接选择排序是一个就地排序

• • • • • • •   需要临时变量temp做交换的中间变量。

（4）稳定性分析

• • • • • • • 直接选择排序是不稳定的

4   归并排序（一个一个分，然后再一对一对的合）

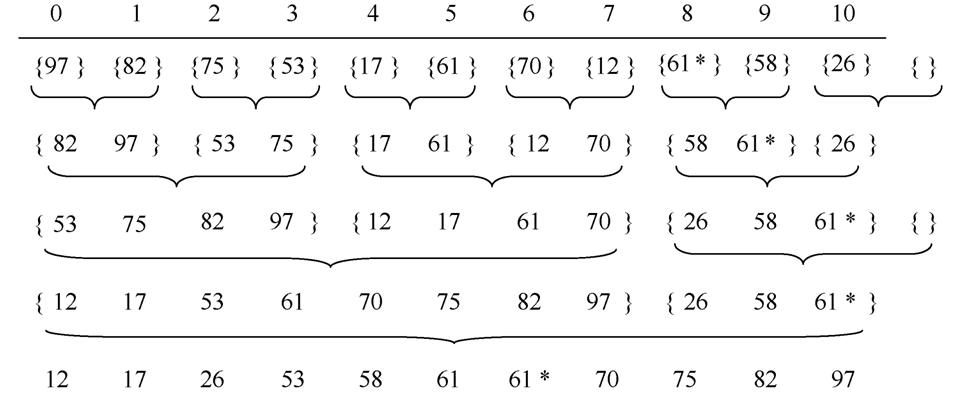
• • • • • • • • • • 归并排序(Merge Sort)是利用“归并”技术来进行排序。
                • 归并：是指将若干个已排序的数据序列合并成一个更大的有序数据序列。
                • 二路归并:将两个已排序的数据序列合并成一个更大的有序数据序列。
              • 1、归并排序算法描述
        • 
          
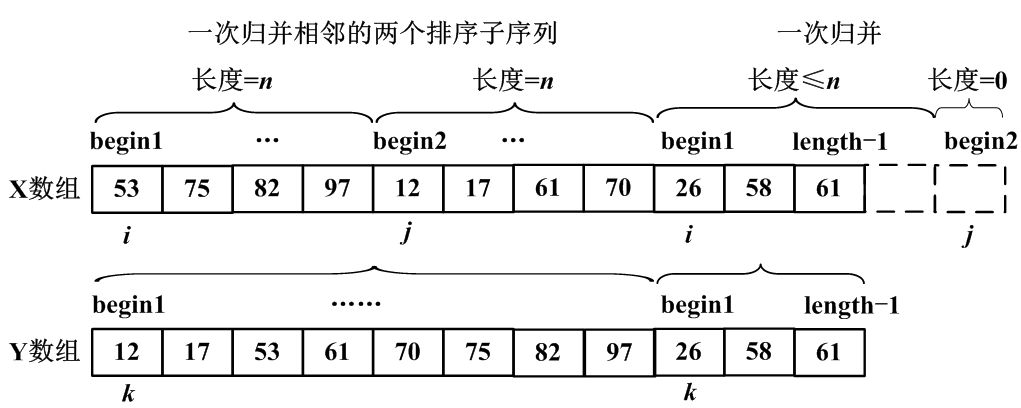
        • 一次归并
        • 
          
        • 2. 归并排序算法实现

          void merge (int[] X, int[] Y, int begin1, int begin2, int n)    //一次归并

          void mergepass(int[] X, int[] Y, int n)

                            //一趟归并，子序列长度为n

          void mergeSort(int[] X)       //归并排序
        • 3、归并排序算法分析

          1、时间复杂度
              　对长度为n的数据序列，需进行趟二路归并，每趟归并的时间为O(n)，故其时间复杂度无论是在最好情况下还是在最坏情况下均是O(nlog2n)。
          2、空间复杂度
             　 需要一个辅助数组来暂存每趟归并的结果，故其辅助空间复杂度为O(n)，显然它不是就地排序。

          3、稳定性
               归并排序是一种稳定的排序。
        • 总结--各种内排序方法的比较和选择

        • • • 1. 按平均时间将排序分为三类：

              （1）平方阶(O(n2))排序
                    一般称为简单排序，例如直接插入、直接  选择和冒泡排序。

              （2）线性对数阶(O(nlog2n))排序
                    如快速、归并排序。

              （3）O(n1+a)阶排序
                    a是介于0和1之间的常数，即0<a<1，如  希尔排序。
            • 2. 影响排序效果的因素

              因为不同的排序方法适应不同的应用环境和要求，所以选择合适的排序方法应综合考虑下列因素：

              • 待排序的数据序列的记录数n；
              • 记录的大小；
              • 关键字的初始状态；
              • 对稳定性的要求；
              • 存储结构；
              • 时间和空间复杂度等。

          3. 不同条件下，排序方法的选择

(1)若n较小(如n≤50)，可采用直接插入或直接选择排序。

• • • • • • • 当记录的大小较小时，直接插入排序较好；
            • 否则因为直接选择移动的记录数少于直接插人，应选直接选择排序为宜。

(2)若数据序列初始状态基本呈现出升序，则应选用直接插入、冒泡排序为宜；

(3)若n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、归并排序。

• 快速排序是目前基于比较的内部排序中被认为是最好的方法，当数据序列的关键字是随机分布时，快速排序的平均时间最短；
• 但是快速排序是不稳定的排序算法。若要求排序稳定，则可选用归并排序。