4种经典位置编码_sinusoidal位置编码和绝对位置编码-CSDN博客

本文链接：https://blog.csdn.net/yinyu19950811/article/details/146180967

显式位置编码

将word ebedding 与position embedding进行拼接，送入到transformer中

缺点：

不具有外推性
需要额外训练一个size：【seq_len， embedding_size】的向量矩阵，占用显存与训练资源

Sinusoidal位置编码

公式：

在这里插入图片描述
这是Transformer原始论文中提出的位置编码方法。它通过使用不同频率的正弦和余弦函数来为每个位置产生一个独特的编码。选择三角函数来生成位置编码有两个良好的性质：

编码相对位置信息，数学上可以证明 $PE_{(pos+k)}$ 可以被 $PE_{(pos)}$ 线性表示，这意味着位置编码中蕴含了相对位置信息。
远程衰减：不同位置的position embedding点乘结果会随着相对位置的增加而递减。
代码：

import numpy as np

def sinusoidal_positional_encoding(max_len, d_model):
    """
    生成Sinusoidal位置编码
    
    参数：
        max_len (int): 序列的最大长度
        d_model (int): 嵌入向量的维度
    
    返回：
        pos_enc (numpy.ndarray): 形状为(max_len, d_model)的位置编码矩阵
    """
    assert d_model % 2 == 0, "d_model必须是偶数"
    
    # 初始化位置编码矩阵
    pos_enc = np.zeros((max_len, d_model))
    
    # 生成位置序列 [0, 1, ..., max_len-1]
    position = np.arange(max_len, dtype=np.float32).reshape(-1, 1)
    
    # 计算除数项，形状为(d_model//2,)
    div_term = np.exp(
        np.arange(0, d_model, 2, dtype=np.float32) * 
        (-np.log(10000.0) / d_model)
    )
    
    # 计算所有位置的角度值
    angle_rads = position * div_term  # 形状：(max_len, d_model//2)
    
    # 应用sin到偶数列，cos到奇数列
    pos_enc[:, 0::2] = np.sin(angle_rads)  # 偶数列
    pos_enc[:, 1::2] = np.cos(angle_rads)  # 奇列
    
    return pos_enc

# 示例用法
if __name__ == "__main__":
    max_len = 50
    d_model = 128
    pe = sinusoidal_positional_encoding(max_len, d_model)
    print(pe.shape)  # 输出：(50, 512)

奇数位

三角函数基础知识

对于标准形式的正弦或余弦函数，它们的基本周期为 $2\pi$ ，也就是说，对于 $y = s in (x)$ ，当 x 增加到
$x+2\pi$ 时，函数的值会重复。

对于一般形式的正弦函数： $y = A s in (B x + c) + D$ ，其中，周期T与B相关，其计算公式为 $T=2\pi/B$ , B是控制频率的参数。 B的绝对值越大，频率越大，周期越小，函数变化得越快。

随位置的变化

对固定的维度i来说，位置pos的变化将影响PE的值。例如，如果我们固定一个维度 $i = 0$ 和 $i = 1$ ，那么正弦和余弦函数将随着位置pos呈现出周期性变化（正弦和余弦是周期函数）。这意味着通过正余弦函数能够区分输入序列中token的不同位置。

随维度的变化

固定位置 pos随着维度i的增加，正弦和余弦函数的频率会降低，周期会变长(见上图)。因此，较低维度具有短的周期，即在较小的位置范围内完成一个周期，换句话说其变化迅速，对小的位移敏感，也就是即使是相邻位置，位置编码的差异也会很大，这有助于模型识别相邻位置间的细微差异。相反，较高维度具有较长的周期，在较大的位置范围内才完成一个周期。变化缓慢，对小的位移不敏感，这能帮助模型感知全局位置关系，捕获长距离依赖。这种多尺度的编码使得Transformer模型能够同时捕捉全局和局部的位置信息。

位置编码向量之间的相似度矩阵:

随着距离变长，内积分数逐渐衰减
在这里插入图片描述
内积分数震荡衰减。

可区分的序列长度

RoPE

详细公式推导：https://zhuanlan.zhihu.com/p/642884818
总结下来就是将q，k向量转换为复数形式，乘以欧拉公式，就可以得到加入位置信息之后q，k的向量内积就是q，k矩阵和旋转矩阵相乘的形式，并且能够代表相对位置编码信息。

所以简单来说 RoPE 的 self-attention 操作的流程是，对于 token 序列中的每个词嵌入向量，首先计算其对应的 query 和 key 向量，然后对每个 token 位置都计算对应的旋转位置编码，接着对每个 token 位置的 query 和 key 向量的元素按照两两一组应用旋转变换，最后再计算 query 和 key 之间的内积得到 self-attention 的计算结果。

与Sinusoidal编码的异同：

Sinusoidal编码是绝对位置编码，RoPE是相对位置编码
更高效：Sinusoidal编码需要将位置向量与词向量相加，再通过矩阵乘法计算注意力分数，可能引入冗余计算；RoPE将位置编码直接融入注意力得分计算中，通过旋转操作修改Query和Key向量，公式上可等价为在点积中引入相对位置项，无需额外存储位置嵌入矩阵。（DeepSeek的回答）
（时间效率有提升吗？乘法加法时间复杂度一致吗？空间效率有提升？）
Sinusoidal编码需要额外计算一个向量 $p_i$ :

RoPE是将位置编码信息融入到q,k中（做矩阵乘法）；

看代码也是额外生成一个矩阵，为什么说无需额外存储位置嵌入矩阵？矩阵乘法的时间复杂度应该大于加法的时间复杂度吧？有同学清楚的帮忙解答一下。

在这里插入图片描述

RoPE外推性更强，RoPE的旋转机制对位置差异的建模具有尺度不变性（相对位置差通过旋转角度体现，与绝对位置无关），因此在处理超出训练时最大长度的序列时表现更稳定。
数学优雅性：RoPE通过旋转矩阵变换（正交变换）更新Query和Key向量，旋转操作不改变向量的模长，从而保持了向量空间的几何性质，避免因位置编码引入的数值偏差。？？详细解释：https://www.zhihu.com/tardis/bd/art/647109286?source_id=1001

Alibi位置编码

Alibi是谷歌发表在ICLR2022的一篇工作，Alibi主要解决了位置编码外推效果差的痛点，算法思想非常的简单，而且非常直观。与直接加在Embedding 上的绝对位置编码不同，
在这里插入图片描述
Alibi的思想是在 Attention score matrix上施加一个与距离成正比的惩罚偏置，惩罚偏置随着相对距离的增加而增加。在具体实现时，对于每个head会有一个超参m 来控制惩罚偏置随着相对距离增加的幅度（斜率）（实现不同head的惩罚程度是有差异的）。
该文提出随着推理token的长度增长，其他模型的困惑度会增加。
在这里插入图片描述
要注意这个惩罚项的值与相似度分数的数值量级要一致。

混合精度下位置编码的bug

从上面的算法原理中，不管是RoPE 的 cos(m \theta) 还是alibi 的 i-1（m, i 代表postion id), 都需要为每个位置生成一个整型的position_id, 在上下文窗口比较大的时候，百川智能发现目前主流的位置编码实现在混合精度下都存在因为低精度（float16/bfloat16)浮点数表示精度不足导致位置编码碰撞的问题。尤其当模型训练（推理）时上下文长度越来越长，低精度表示带来的位置编码碰撞问题越来越严重，进而影响模型的效果.
bfloat16表示的不同数值范围时表示的数据精度，可以看到当数值>256时，无法表示一个整数。这样当序列长度变长时，会造成位置碰撞。

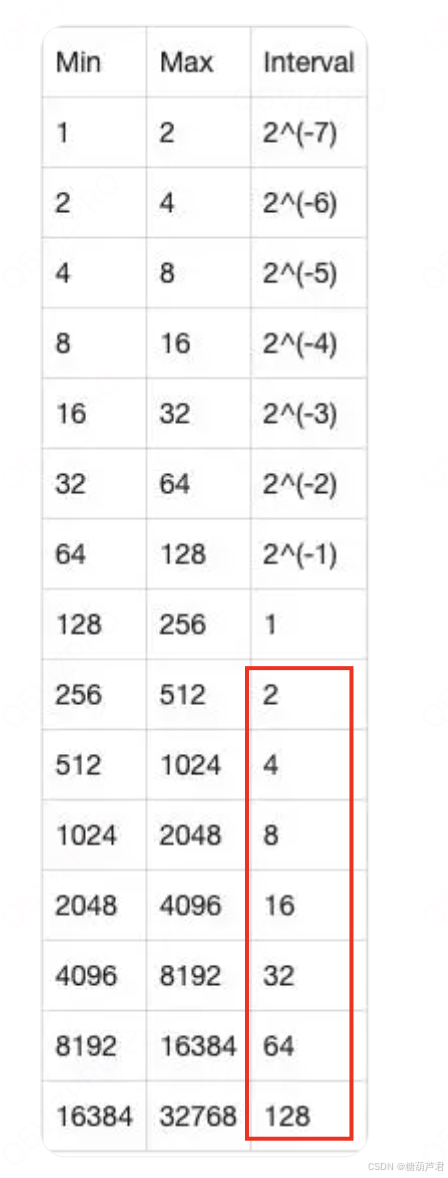
根据bfloat16的表示精度可知，训练（推理）时上下文长度越长，位置编码碰撞的情况越严重，长度为8192的上下文推理中，仅有大约10%的token位置编码是精确的，好在位置编码碰撞有局域性的特质，只有若干个相邻的token才会共享同一个position Embedding, 在更大的尺度上，不同位置的token 还是有一定的区分性。

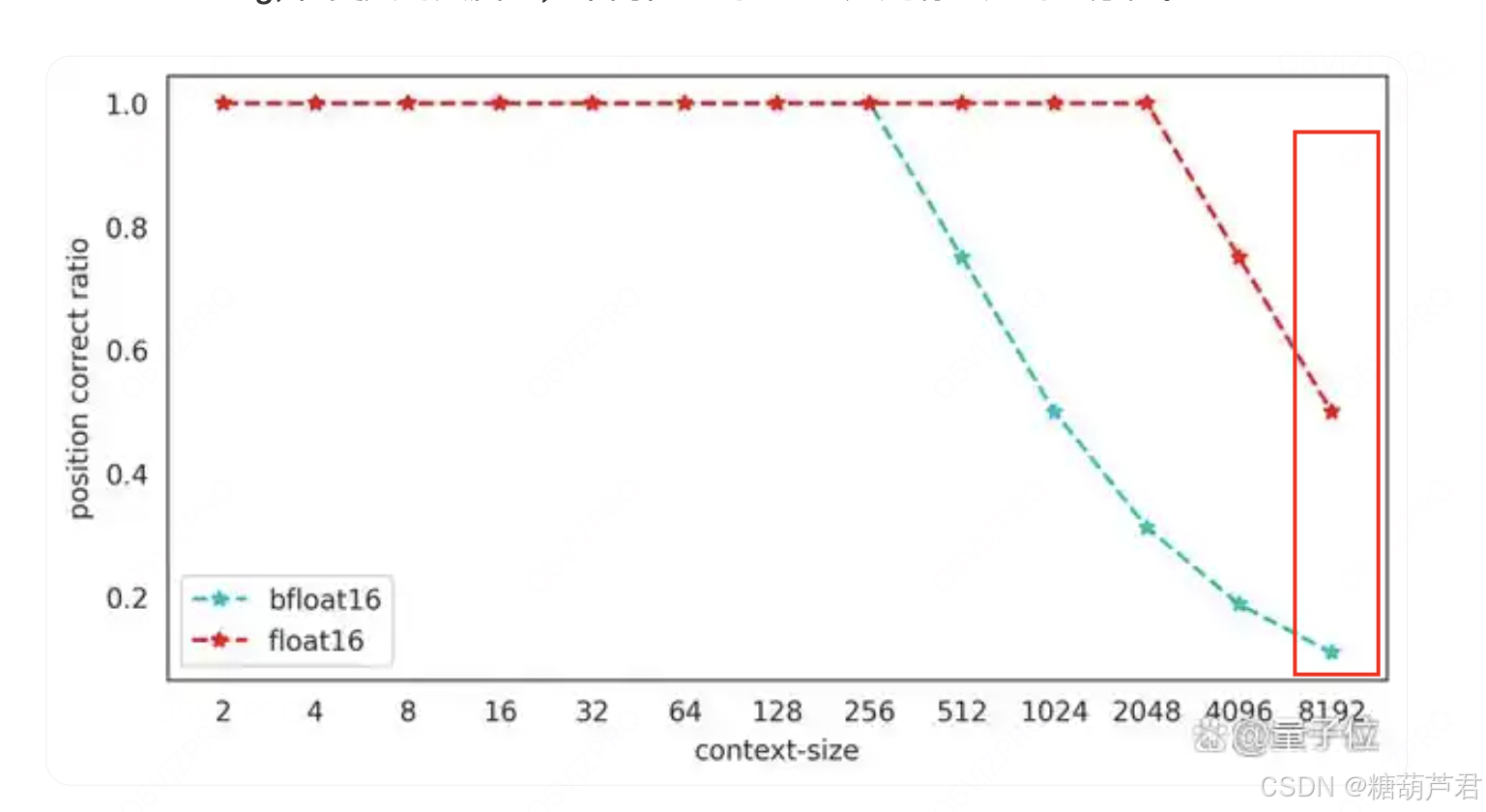
参考：

混合精度下位置编码竟有大坑，LLaMA等主流开源模型纷纷中招
Alibi ： TRAIN SHORT, TEST LONG: ATTENTION WITH LINEAR
BIASES ENABLES INPUT LENGTH EXTRAPOLATION
https://baijiahao.baidu.com/s?id=1774904299506648763&wfr=spider&for=pc
正弦余弦位置编码：https://zhuanlan.zhihu.com/p/580739696
https://www.zhihu.com/tardis/bd/art/647109286?source_id=1001
PoPE： Roformer: Enhanced Transformer With Rotray Position Embedding