基于地图的深度优先、广度优先、Dijkstra算法Java实现。

最新推荐文章于 2024-10-01 15:02:37 发布
最新推荐文章于 2024-10-01 15:02:37 发布
阅读量5.4k 收藏 3
点赞数
分类专栏： 算法学习 文章标签： 算法 java string 扩展 游戏 import
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/yinzhuo1/article/details/7177456
版权

       本文主要通过基于一张简单的游戏地图，实现深度优先、广度游戏、Dijkstra算法（说明：主要参考了别人滴代码，自己改写了下）。    

 深度优先算法， 先附截图一张：

           

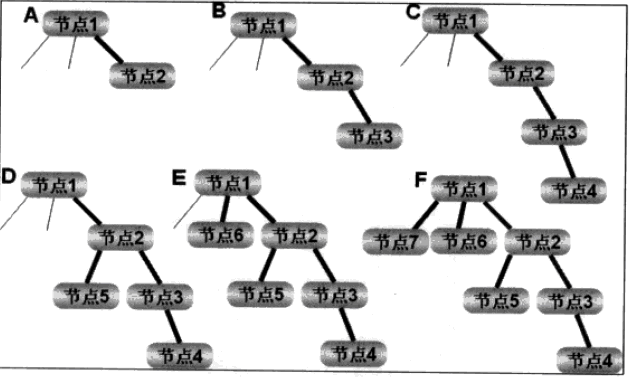
  深度优先搜索算法在搜索过程中不考虑各个边的开销，只考虑路径的选择，基本思路是：站在一个连通图的的一个节点上，然后尽可能的沿着一条边深入，当遇到死角时回溯，然后继续搜索，直到搜索到目的节点为止，深度优先一般使用栈结构实现，结合上面滴图 ， 应该比较容易理解了。


广度优先搜索，  在附截图一张   ：

              

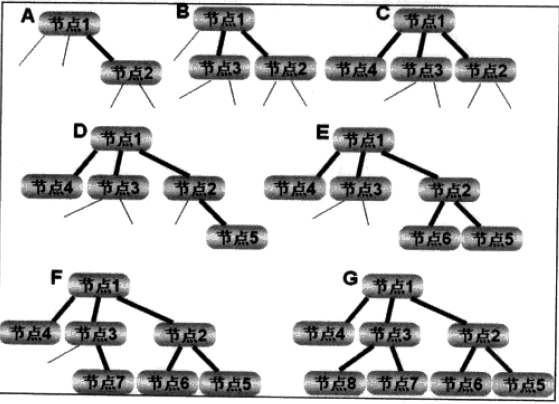
从图就可以很显然的看出，广度优先和深度优先的不同，广度优先是：在一个连通图的节点上依次向下遍历它所有的子节点，直到找到目的节点为止。广度优先一般使用队列结构实现。


             

Dijkstra算法，依然附上截图二张：

 

    


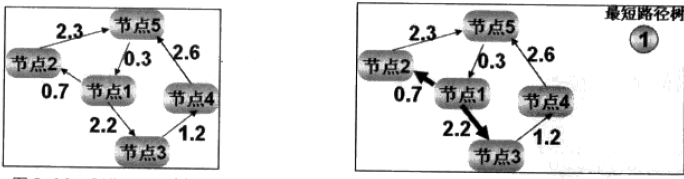
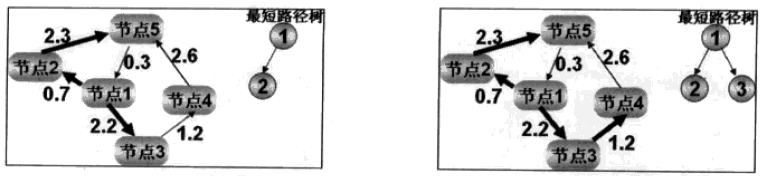
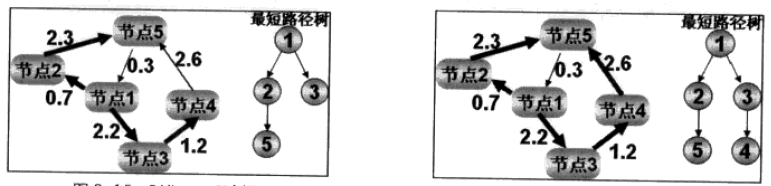
Dijkstra是典型的最短路径搜索算法，一般是从一点出发到另外一点的最短路径，但是它遍历的节点数太多，效率比较底。

分析一下上图： 从节点1出发：可以到达节点为节点3、节点2，比较他们到节点1的距离，将较小的节点2加入最短路径树。在依次比较节点5和节点3的大小，将较小的节点3加入最短路径数，继续比较下去直到搜索到目的节点。


前面滴分析，可能表达滴不太好。 下面是我修改了滴源码，是基于一张简单的地图，在地图上搜索目的节点，依次用深度优先、广度优先、Dijkstra算法实现。


import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.PriorityQueue;
import java.util.Stack;


/**
 * 
 * @author yinzhuo
 *
 */
public class Arithmatic {
boolean flag = true;
// 一张地图
static int[][] map = new int[][]// 地图数组
{
{ 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0 },
{ 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0 },
{ 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0 },
{ 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0 },
{ 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0 },
{ 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } };



//深度优先所使用的栈
Stack<int[][]> stack = new Stack<int[][]>();
HashMap<String,int[][]> hm=new HashMap<String,int[][]>();//结果路径记录
//出发点
int[] source = {2,2};
//目标点
int[] target = {21,22};
//已经访问过的点
int[][] visited=new int[map.length][map[0].length];//0 未去过 1 去过
//当前点的八方
int[][] sequence={
{0,1},{0,-1},
{-1,0},{1,0},
{-1,1},{-1,-1},
{1,-1},{1,1}
};
//访问经过的路径总长度
int count = 0;
LinkedList<int[][]> queue = new LinkedList<int[][]>();

//记录到每个点的最短路径 for Dijkstra
HashMap<String,ArrayList<int[][]>> hmPath=new HashMap<String,ArrayList<int[][]>>();
//记录路径长度 for Dijkstra
int[][] length=new int[map.length][map[0].length];


/**
 * @param args
 */
public static void main(String[] args) {
Arithmatic a = new Arithmatic();
System.out.println("-----------深度优先搜索算法实现---------");
a.DFS();
System.out.println(a.count);

int[] temp = a.target;
while(true){
int[][] tempA=a.hm.get(temp[0]+":"+temp[1]);
System.out.println("(" + tempA[0][0] + "," + tempA[0][1] + ")" + "--" + "(" + tempA[1][0] + "," + tempA[1][1] + ")");
if(tempA[1][0]==a.source[0]&&tempA[1][1]==a.source[1]){//判断有否到出发点
break;
}
temp=tempA[1];
}

// for(int i = 0; i < a.stack.size(); i++){
// System.out.println("(" + a.stack.get(i)[0][0] + "," + a.stack.get(i)[0][1] + ")" + "--" + "(" + a.stack.get(i)[1][0] + "," + a.stack.get(i)[1][1] + ")");
// }
a.visited=new int[map.length][map[0].length];
System.out.println("-----------广度优先搜索算法实现---------");
a.BFS();
System.out.println(a.count);
temp = a.target;
while(true){
int[][] tempA=a.hm.get(temp[0]+":"+temp[1]);
System.out.println("(" + tempA[0][0] + "," + tempA[0][1] + ")" + "--" + "(" + tempA[1][0] + "," + tempA[1][1] + ")");
if(tempA[1][0]==a.source[0]&&tempA[1][1]==a.source[1]){//判断有否到出发点
break;
}
temp=tempA[1];
}
// for(int i = 0; i < a.queue.size(); i++){
// System.out.println("(" + a.queue.get(i)[0][0] + "," + a.queue.get(i)[0][1] + ")" + "--" + "(" + a.queue.get(i)[1][0] + "," + a.queue.get(i)[1][1] + ")");
// }

a.visited=new int[map.length][map[0].length];
System.out.println("----------Dijkstra算法实现--------------");
a.Dijkstra();
System.out.println(a.count);
ArrayList<int[][]> alPath=a.hmPath.get(a.target[0]+":"+a.target[1]);
for(int[][] t: alPath){
System.out.println("(" + t[0][0] + "," + t[0][1] + ")" + "--" + "(" + t[1][0] + "," + t[1][1] + ")");
}

}


/**
 * 深度优先搜索算法
 */
public void DFS() {
//开始路径
int[][] start = {{source[0],source[1]},{source[0],source[1]}};
stack.push(start);
while(flag){
int[][] currentEdge=stack.pop();//从栈顶取出边
int[] tempTarget=currentEdge[1];//取出此边的目的点
//判断目的点是否去过，若去过则直接进入下次循环
if(visited[tempTarget[1]][tempTarget[0]]==1){
continue;
}
count++;
visited[tempTarget[1]][tempTarget[0]]=1;//标识目的点为访问过
//记录此临时目的点的父节点
hm.put(tempTarget[0]+":"+tempTarget[1],new int[][]{currentEdge[1],currentEdge[0]});
//判断有否找到目的点
if(tempTarget[0]==target[0]&&tempTarget[1]==target[1]){
break;
}
//将所有可能的边入栈
int currCol=tempTarget[0];
int currRow=tempTarget[1];
//将它的周围相连点都加入到栈中
for(int[] rc:sequence){
int i=rc[1];
int j=rc[0];
if(i==0&&j==0){continue;}
if(currRow+i>=0&&currRow+i<map.length&&currCol+j>=0&&currCol+j<map[0].length&&
map[currRow+i][currCol+j]!=1){
//将此边入栈
int[][] tempEdge={
{tempTarget[0],tempTarget[1]},
{currCol+j,currRow+i}
};
stack.push(tempEdge);
}
}
}
}

/**
 * 深度优先算法
 */
public void BFS(){
count = 0;
hm.clear();

//开始路径
int[][] start = {{source[0],source[1]},{source[0],source[1]}};
queue.offer(start);
while(flag){
int[][] currentEdge=queue.poll();//从队首取出边
int[] tempTarget=currentEdge[1];//取出此边的目的点
//判断目的点是否去过，若去过则直接进入下次循环
if(visited[tempTarget[1]][tempTarget[0]]==1){
continue;
}
count++;
visited[tempTarget[1]][tempTarget[0]]=1;//标识目的点为访问过
//记录此临时目的点的父节点
hm.put(tempTarget[0]+":"+tempTarget[1],new int[][]{currentEdge[1],currentEdge[0]});
//判断有否找到目的点
if(tempTarget[0]==target[0]&&tempTarget[1]==target[1]){
break;
}
//将所有可能的边入队列
int currCol=tempTarget[0];
int currRow=tempTarget[1];
for(int[] rc:sequence){
int i=rc[1];
int j=rc[0];
if(i==0&&j==0){continue;}
if(currRow+i>=0&&currRow+i<map.length
&&currCol+j>=0&&currCol+j<map[0].length&&
map[currRow+i][currCol+j]!=1){
int[][] tempEdge={
{tempTarget[0],tempTarget[1]},
{currCol+j,currRow+i}
};
queue.offer(tempEdge);
}
}
}
}

/**
 * 广度优先A*算法
 */
public void BFSAStar(){

}

/**
 * Dijkstra算法
 */
public void Dijkstra(){

for(int i=0;i<length.length;i++){
for(int j=0;j<length[0].length;j++){
length[i][j]=9999;//初始路径长度为最大距离都不可能的那么大
}
}
count = 0;

int[] start={source[0],source[1]};//开始点col,row
visited[source[1]][source[0]]=1;
for(int[] rowcol:sequence){//计算此点所有可以到达点的路径及长度
int trow=start[1]+rowcol[1];
int tcol=start[0]+rowcol[0];
//超出地图
if(trow<0||trow>18||tcol<0||tcol>18)continue;
//碰到墙壁
if(map[trow][tcol]!=0)continue;
//记录路径长度
length[trow][tcol]=1;
//计算路径
String key=tcol+":"+trow;
ArrayList<int[][]> al=new ArrayList<int[][]>();
al.add(new int[][]{{start[0],start[1]},{tcol,trow}});
hmPath.put(key,al);
count++;
}
//bre跳出循环标记
bre:while(flag){
//找到当前扩展点K 要求扩展点K为从开始点到此点目前路径最短，且此点未考察过
int[] k=new int[2];
int minLen=9999;
for(int i=0;i<visited.length;i++){
for(int j=0;j<visited[0].length;j++){
if(visited[i][j]==0){
if(minLen>length[i][j]){
minLen=length[i][j];
k[0]=j;//col
k[1]=i;//row
}
}
}
}
visited[k[1]][k[0]]=1;//设置去过的点
int dk=length[k[1]][k[0]];//取出开始点到K的路径长度
ArrayList<int[][]> al=hmPath.get(k[0]+":"+k[1]);//取出开始点到K的路径
//循环计算所有K点能直接到的点到开始点的路径长度
for(int[] rowcol:sequence){
int trow=k[1]+rowcol[1];//计算出新的要计算的点的坐标
int tcol=k[0]+rowcol[0];
//若要计算的点超出地图边界或地图上此位置为障碍物则舍弃考察此点
if(trow<0||trow>map.length-1||tcol<0||tcol>map[0].length-1)continue;
if(map[trow][tcol]!=0)continue;
int dj=length[trow][tcol];//取出开始点到此点的路径长度
int dkPluskj=dk+1;//计算经K点到此点的路径长度
//若经K点到此点的路径长度比原来的小则修改到此点的路径
if(dj>dkPluskj){
String key=tcol+":"+trow;
//克隆开始点到K的路径
ArrayList<int[][]> tempal=(ArrayList<int[][]>)al.clone();
//将路径中加上一步从K到此点
tempal.add(new int[][]{{k[0],k[1]},{tcol,trow}});
//将此路径设置为从开始点到此点的路径
hmPath.put(key,tempal);
//修改到从开始点到此点的路径长度
length[trow][tcol]=dkPluskj;
//若此点从未计算过路径长度则将此点加入考察过程记录
if(dj==9999){//将去过的点记录
count++;
}
}
//看是否找到目的点
if(tcol==target[0]&&trow==target[1]){
//终止循环
break bre;
}
}
}

}



}


蓝雾
关注
专栏目录
蓝桥杯:外卖店优先级(map排序算法) Java
weixin_50165209的博客
02-27 721
算法题:外卖店的优先级
Java实现深度优先遍历和广度优先遍历
李利科
12-23 1911
概念定义： 深度优先遍历：深度优先遍历是图论中的经典算法。其利用了深度优先搜索算法可以产生目标图的相应拓扑排序表，采用拓扑排序表可以解决很多相关的图论问题，如最大路径问题等等。 深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点(即那些不包含任何超链的HTML文件) 。在一个HTML文件中，当一个超链被选择后，被链接的HTML文件将执行深度优先搜索，即在搜索其余的超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止，然后返回到某一个
Java实现二叉树的深度优先遍历和广度优先遍历算法示例
08-27
主要介绍了Java实现二叉树的深度优先遍历和广度优先遍历算法,结合实例形式详细分析了二叉树的定义、深度优先遍历与广度优先遍历算法原理与相关操作实现技巧,需要的朋友可以参考下
一文彻底搞懂Dijkstra算法（迪杰斯特拉算法）
最新发布
数据结构和算法教程（C语言版）
10-01 1325
Dijkstra算法（迪杰斯特拉算法）可以在给定网（带权图）中查找一个顶点到其它顶点的最短路径，算法的时间复杂度为O(n^2)。如果需要查找网中任意两个顶点之间的最短路径，虽然Dijkstra算法也能解决（对每个顶点都执行一次Dijkstra算法），但更建议使用Floyd弗洛伊德算法。t=O83A图存储结构，数据结构中的图从本节开始，我将为大家介绍最后一种存储结构，也是数据结构中最复杂、难掌握的存储结构 图。图结构常用来存储逻辑关系为多对多的数据。
基于谷歌地图的Dijkstra算法水路路径规划
weixin_34262482的博客
04-27 211
　　最终效果图如下： 还是图、邻接表，可以模拟出几个对象=》节点、边、路径。三个类分别如下： Node 节点： using System; using System.Collections.Generic; namespace Road.Plan { public class Node { private string id; ...
Java实现深度优先搜索（Depth-First Search，DFS）算法
zy0412326的专栏
07-24 437
Java实现深度优先搜索（Depth-First Search，DFS）算法深度优先搜索（Depth-First Search, DFS）是一种用于遍历或搜索树或图的算法。
java实现深度优先搜索 (DFS) 算法
小筱在线博客
12-24 1205
度优先搜索（Depth First Search，DFS）算法是一种用于遍历或搜索图或树的算法。这种算法从一个节点开始，沿着一条路径尽可能深地搜索，直到遇到不能继续前进的节点时返回上一个节点，然后继续搜索其他路径。然后，我们实现了递归和迭代版本的DFS。递归版本的DFS使用了一个辅助函数DFSUtil来进行递归的深度优先搜索。在Main函数中，我们创建了一个具有6个顶点的图，并添加了几条边。接着，我们分别调用了递归和迭代版本的DFS来进行深度优先搜索。本示例中，我们首先创建了一个Graph类表示图。
广度优先搜索算法介绍和java代码实现
06-30
2. 对于有权图（边的权重不相等），BFS可能不是最优解决方案，此时更适合使用深度优先搜索（DFS）或Dijkstra算法。 适用场景： 1. 在无权图中寻找最短路径或最少步骤的问题，如迷宫问题。 2. 在网络路由问题中，...
深度优先搜索算法介绍和Java代码实现
06-30
- **非最短路径**：DFS并不保证找到的是最短路径，如果需要找到最短路径，通常会使用Dijkstra算法或其他最优化算法。 6. **Java代码实现** 在提供的Java代码中，首先定义了一个`Node`类，表示图中的节点，包含值...
Java实现图的深度优先搜索与广度优先搜索
"Java编程实现基于图的深度优先搜索和广度优先搜索的完整代码，适用于15puzzle问题和其他类似问题的解决。" 在计算机科学中，图是一种数据结构，用于表示对象之间的关系。深度优先搜索（DFS）和广度优先搜索（BFS）...
图的深度优先和广度优先遍历源码
10-11
本资料包含的是Java实现的图的深度优先遍历（DFS, Depth First Search）和广度优先遍历（BFS, Breadth First Search）的源码，方便开发者直接运行和学习。 深度优先遍历是从一个顶点出发，尽可能深地搜索图的分支。...
（有向）图的深度优先遍历算法模板算法(java源码)
01-21
/* * （有向）图的深度优先遍历算法模板 */ package dsa; public abstract class DFS extends GraphTraverse { //变量 protected static int clock = 0;//遍历过程中使用的计时钟 //构造方法 public DFS(Graph g) { super(g); } //深度优先遍历算法 protected Object traverse(Vertex v, Object info) {//从顶点v出发，做深度优先查找 if (UNDISCOVERED != v.getStatus()) return null;//跳过已访问过的顶点（针对非连通图） v.setDStamp(clock++); v.setStatus(DISCOVERED); visit(v, info);//访问当前顶点 for (Iterator it = v.outEdges(); it.hasNext();) {//检查与顶点v Edge e = (Edge)it.getNext();//通过边e = (v, u) Vertex u = (Vertex)e.getVPosInV(1).getElem();//相联的每一顶点u switch (u.getStatus()) {//根据u当前的不同状态，分别做相应处理 case UNDISCOVERED ://若u尚未被发现，则 e.setType(TREE);//e被归类为“树边” traverse(u, info);//从u出发，继续做深度优先查找 break; case DISCOVERED ://若u已经被发现，但对其访问尚未结束，则 e.setType(BACKWARD);//将e归类为“后向跨边” break; default ://VISITED，即对u的访问已经结束 if (u.getDStamp() < v.getDStamp())//若相对于v，u被发现得更早，则 e.setType(CROSS);//将e归类为“横跨边” else//否则 e.setType(FORWARD);//将e归类为“前向跨边” break; } }//至此，v的所有邻居都已访问结束，故 v.setFStamp(clock++); v.setStatus(VISITED);//将v标记为VISITED return null;//然后回溯 } }
Dijkstra Algorithm·深度优先算法python3编译
fStardust的博客
12-07 269
深度优先算法 Dijkstra Algorithm *本算法与《算法图解》书中代码并无多少差别；python 3.8 与python 2.7在本代码中差别体现在中间试运行时的输出差别，也并不大。 深度优先算法与广度优先算法的区别在于： “深度”：要走完所有节点及相关通路，得出花销最小的通道； “广度”：每次遍历一层，得到结果后便输出结果，得出的是通过节点数最少的通道。 # DijkstraAlgorithm # 狄科斯特拉算法·深度优先算法 # 主要特点是从起始点开始，采用贪心算法的策略， # 每次遍历到始
图论学习笔记——Dijkstra(广度优先)
计算机小白努力学习
05-06 1675
1.Dijkstra(广度优先) Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。 问题描述：在无向图 G=(V,E) 中，假设每条边...
Java实现深度优先搜索
m0_52884709的博客
11-19 2260
图的遍历就是访问图中的每个节点并且每个节点只访问一次。但图中有那么多节点，要如何进行访问就是一个问题，所以我们需要有特定的策略来进行访问这些节点。我们将要访问的节点成为头节点，相邻节点称为表节点；头节点中存储数据和第一个表节点，表节点中存储头节点的下标和头节点的下一个相邻节点；从初始节点开始出发访问，访问该节点的第一个相邻节点，然后以该相邻节点为起点，继续访问其相邻节点，反复持续该过程直到图中所有节点已全部被访问；，注意：深度优先搜索的顺序不是唯一的，这取决于访问起点和表节点的顺序。在main方法中测试。
一个基于Dijkstra算法的路径规划大作业
daylight714的博客
11-18 1518
基于Dijkstra算法的路径规划大作业 对医院轨道传输系统进行环境建模，通过抽象表达，集合各个路径、节点的属性，选择Dijkstra算法作为关键路径规划算法，设计一种简单的规则来解决多TV间的冲突。 背景 医院的轨道物流系统Track Vehicle System (TVS)是一个鲜为人知但很有潜力的研究方向，这样一个系统将住院部、急诊室、护士室、手术室、检验科、血库、中心药房等站点连接起来，利用物联网技术完成对小车的智能控制以及系统中各个实体之间的通信交互，而无需人为干涉。 问题 这里将问题抽象，并进
java 语言实现深度优先搜索（DFS）图算法
微笑的 Java
08-30 967
在这个示例中，我们使用了一个栈来保存待访问的节点。在每次循环中，我们从栈中弹出一个节点，并将其标记为已访问。然后，我们迭代该节点的邻居节点，如果邻居节点尚未被访问，则将其压入栈中。深度优先搜索算法的核心思想是递归地探索每个节点的邻居节点，直到到达最深处，然后再回溯到上一个节点，继续探索其他未被访问的节点。然后，我们迭代该节点的邻居节点，如果邻居节点尚未被访问，则递归调用。在深度优先搜索中，使用栈数据结构来保存待访问的节点。方法中，我们创建一个示例图，并从节点0开始进行深度优先搜索。方法中，我们创建一个。
java实现图的深度优先搜索算法
小溪科技
04-05 932
/****************************************************************************** * Compilation: javac DepthFirstSearch.java * Execution: java DepthFirstSearch filename.txt s * Dependencies: G
深度搜索 java_Java中的深度优先搜索
weixin_30252651的博客
02-21 1449
1. 概述在本教程中，我们将探讨Java中的深度优先搜索深度优先搜索(DFS)是一个应用于树、图等数据结构的遍历算法。在移动到下一个分支之前，深度优先搜索会 深度为优先原则去探索新的分支。在接下来的部分中，我们将首先了解树的实现，然后是图。要了解如何在Java中实现这些结构，请查看我们以前的关于 二叉树 Binary Tree 和 图 Graph 的教程。2. 树的深度优先搜索使用 DFS 遍历树...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值