From https://zhuanlan.zhihu.com/p/42006406
Viterbi Algorithm(维特比算法)
如果target sequence词汇表的大小为  的话,对于解码器的
的话,对于解码器的  步输出,他的搜索空间
步输出,他的搜索空间 。随着
。随着  的增大,那这个效率会非常低。所以我们才想要通过一些算法去找出使得概率最大的输出序列。
的增大,那这个效率会非常低。所以我们才想要通过一些算法去找出使得概率最大的输出序列。
如果我们把  看成是三个状态:
看成是三个状态:
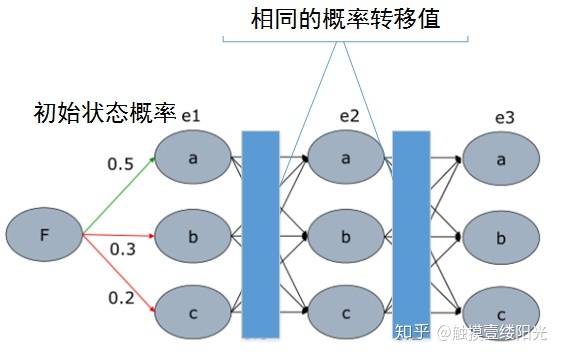
HMM
那可以看成是HMM,对于HMM来说,求给定观测序列条件概率  最大的状态序列,属于HMM的第三个基本问题~预测问题。在HMM中,我们使用了Viterbi Algorithm。那类似的,我们会想到使用Viterbi Algorithm应用到求最大序列的问题上。
最大的状态序列,属于HMM的第三个基本问题~预测问题。在HMM中,我们使用了Viterbi Algorithm。那类似的,我们会想到使用Viterbi Algorithm应用到求最大序列的问题上。
Viterbi Algorithm用动态规划的思想来求解概率最大的路径(最优路径),这个最终的最优路径就是我们想要得到的最终的输出序列。简单的说我们只需从第1步开始,递推地计算在第  步输出单词为
步输出单词为  的各条部分路径的最大概率,直至得到最后一步输出单词
的各条部分路径的最大概率,直至得到最后一步输出单词  的各条路径的最大概率。下面使用一个简单的例子来说明一下Viterbi Algorithm:
的各条路径的最大概率。下面使用一个简单的例子来说明一下Viterbi Algorithm:
那假设现在只有两个单词,即  ,那么我们可以画出下面的概率图模型出来(这里为了简单,状态转移值):
,那么我们可以画出下面的概率图模型出来(这里为了简单,状态转移值):

我们想得到最优路径(路径上概率值乘积最大),根据动态规划的思想那么可以认为每一步都是最优的。我们可以发现每一个节点都对应着部分路径,比如对于第二步来说:
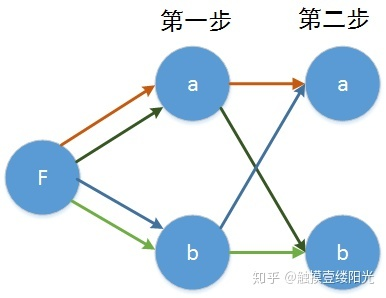
- 对于第二步的
 结点来说:
结点来说:  ,
,  两条路径,那现在假设
两条路径,那现在假设  的值最大,也即认为对于第二步的
的值最大,也即认为对于第二步的  结点来说
结点来说 是最优的序列;
是最优的序列; - 对于第二步的
 结点来说:
结点来说:  ,
,  两条路径,那现在假设
两条路径,那现在假设  的值最大,也即认为对于第二步的
的值最大,也即认为对于第二步的  结点来说
结点来说 是最优的序列;
是最优的序列;
对于第二步的每一个节点我们都有了一个对于这个结点来说最优的序列,那现在我们加上第三步:

- 对于第三步的
 结点来说:
结点来说:  ,
,  ,
,  ,
,  四条路径:
四条路径: - 对于
 ,
,  这两条路径来说,因为我们前面在第二步的
这两条路径来说,因为我们前面在第二步的  结点中已经确定了到达第二步结点
结点中已经确定了到达第二步结点  时候的最优路径,所以我们选择
时候的最优路径,所以我们选择 这条路径;
这条路径; - 对于
 ,
,  这两条路径来说,因为我们前面在第二步的
这两条路径来说,因为我们前面在第二步的  结点中已经确定了到达第二步结点
结点中已经确定了到达第二步结点  时候的最优路径,所以我们选择
时候的最优路径,所以我们选择 这条路径;
这条路径;
然后我们可以知道对于第三步的  结点来说,是
结点来说,是  大还是
大还是  概率值大,选择最大的概率值对应的序列作为第三步结点
概率值大,选择最大的概率值对应的序列作为第三步结点  的最优路径。这样不断的迭代知道最后一步,选择概率最大的结点最为最终的最优路径。当然我们需要的是使得最终概率值最大的序列,所以我们需要计算每一个结点最优路径的时候,需要记住保留路径的父节点,比如对于第二步的
的最优路径。这样不断的迭代知道最后一步,选择概率最大的结点最为最终的最优路径。当然我们需要的是使得最终概率值最大的序列,所以我们需要计算每一个结点最优路径的时候,需要记住保留路径的父节点,比如对于第二步的  结点来说,我们得到
结点来说,我们得到  最为最优路径,那对于第二步的
最为最优路径,那对于第二步的  结点来说,我们需要记住被选择的父节点也就是第一步的
结点来说,我们需要记住被选择的父节点也就是第一步的  结点。
结点。
有了上面简单的介绍,现在我们用公式来定义:
 表示以
表示以  结尾的最大概率的sequence的概率;
结尾的最大概率的sequence的概率; 表示第
表示第  步从
步从  到第
到第  步的
步的  的概率,也就是转移概率,在概率图模型中就是
的概率,也就是转移概率,在概率图模型中就是  和
和  路径上的概率值;
路径上的概率值;
动态规划的递推公式:


下面来看一看使用Viterbi算法的复杂度:
- 从上面的表格可以看出计算复杂度为
 ,那对于表格中的每一个单元,需要从前面的
,那对于表格中的每一个单元,需要从前面的  的数据中去遍历,所以计算复杂度为
的数据中去遍历,所以计算复杂度为  。比如对于
。比如对于 ![s(a,2)[a]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) 来说,计算这个值我们需要计算
来说,计算这个值我们需要计算  也就是需要去遍历出
也就是需要去遍历出 ;
; - 空间复杂度也就是表格中所有数据,即空间复杂度
 ;
;
那可以看出,Viterbi算法还是很不错的,能够得到最优的值,但是如果target sequence词汇表  特别大的话,效率还是不高,当然target sequence词汇表
特别大的话,效率还是不高,当然target sequence词汇表  很小的时候,Viterbi算法会是一个很不错的选择,但是通常我们的target sequence词汇表
很小的时候,Viterbi算法会是一个很不错的选择,但是通常我们的target sequence词汇表  很大。所以就有了Beam search算法,他通过舍弃一些精度来提高效率。
很大。所以就有了Beam search算法,他通过舍弃一些精度来提高效率。
Beam Search算法
beam search方法中有一个关键的参数Beam Size B,这个B是远远小于  的,即
的,即  。对于Viterbi算法我们填一个
。对于Viterbi算法我们填一个  的表格,那其实对于beam search算法来说我们填的是一个
的表格,那其实对于beam search算法来说我们填的是一个  的表格。直观的来看beam search比Viterbi算法效率高很多,因为
的表格。直观的来看beam search比Viterbi算法效率高很多,因为 。
。
我们还是通过例子来说明算法的流程,然后使用给出公式定义来,还是使用下面的概率图模型来说说明:
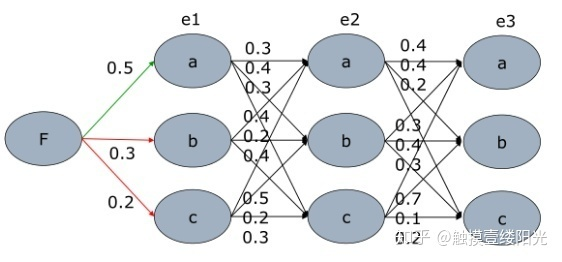
我们还是要找出使得  最大的序列
最大的序列  ,现在假定beam search参数
,现在假定beam search参数  ,那么会有:
,那么会有:
第一步输出(B = 2):

第一步执行流程
第二步输出(B = 2):

第二步执行流程
第三步输出(B = 2):

第三步执行流程
从最后一步的输出结果可以看出,最终输出的序列为  。知道了beam search的执行流程,下面给出公式定义:
。知道了beam search的执行流程,下面给出公式定义:
 在
在  位置的已经生成的sequence;
位置的已经生成的sequence;
递推公式:已知  和
和  ,求:
,求:  ,执行步骤如下:
,执行步骤如下:
![temp = [(h(b,n) + v,P(h(b,n)+v) | b = 1,...,B,v = 1,...,V)]](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ;
;![temp = sort(temp,key = lambda x:[1])](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ,以概率值进行排序;
,以概率值进行排序;![b(i,n+1),s(i,n+1) = temp[i],i = 1,...,B](https://i-blog.csdnimg.cn/blog_migrate/1dc060f5942fc9819ab32b2950270756.png) ;
;
前面定义了这么多变量,那下面那上面的第二步输出说明一下这些变量表示的具体含义:

那看看beam search算法的复杂度:
- 计算复杂度
 ,我们是按列进行填写的,所以需要计算
,我们是按列进行填写的,所以需要计算  个,我们对
个,我们对  进行排序的是
进行排序的是  ,所以是
,所以是  ,所以每一列的计算复杂度是
,所以每一列的计算复杂度是  ,那总共有
,那总共有  列,所以计算复杂度为
列,所以计算复杂度为 ;
; - 空间复杂度就是表格中需要填的元素个数,所以空间复杂度为
 ;
;
那可以看出,beam search算法还是很不错的,他得到的结果是近似的最优解,如果target sequence词汇表  特别大的话,他的计算复杂度也不会太大,所以效率上比Viterbi算法和贪心算法要高的很多。
特别大的话,他的计算复杂度也不会太大,所以效率上比Viterbi算法和贪心算法要高的很多。








 本文深入探讨了维特比算法与束搜索算法在序列解码中的应用,对比了两者在不同场景下的效率与准确性,尤其适用于目标序列词汇表较大情况下的优化策略。
本文深入探讨了维特比算法与束搜索算法在序列解码中的应用,对比了两者在不同场景下的效率与准确性,尤其适用于目标序列词汇表较大情况下的优化策略。
















 3505
3505

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








