归并排序-大事化小

归并排序

前情回顾

前面介绍了几种简单的排序方法

• 选择排序
• 插入排序
• 希尔排序
  今天的主角是叫做归并排序的一种方法，归并排序最吸引人的性质是它能保证将任意长度为N的数组排序所需时间和 NlogN成正比，而这是其他排序算法复杂度的上限；而它的主要缺点是它所需的额外空间和N成正比。

算法动图

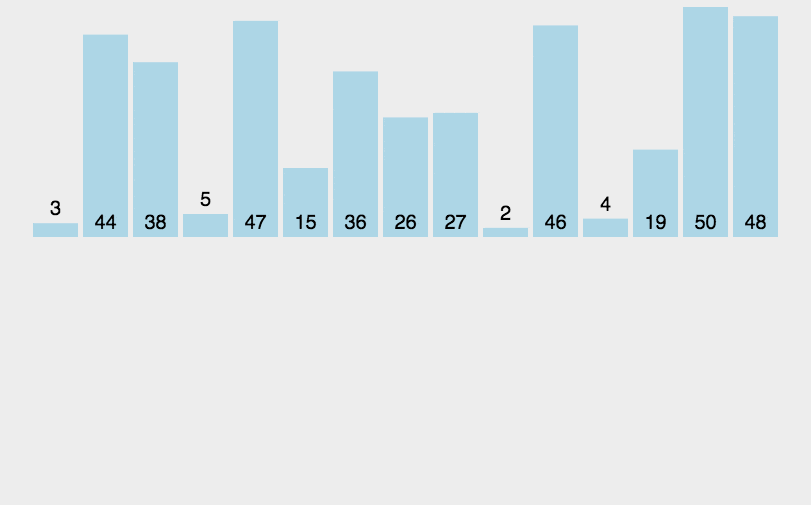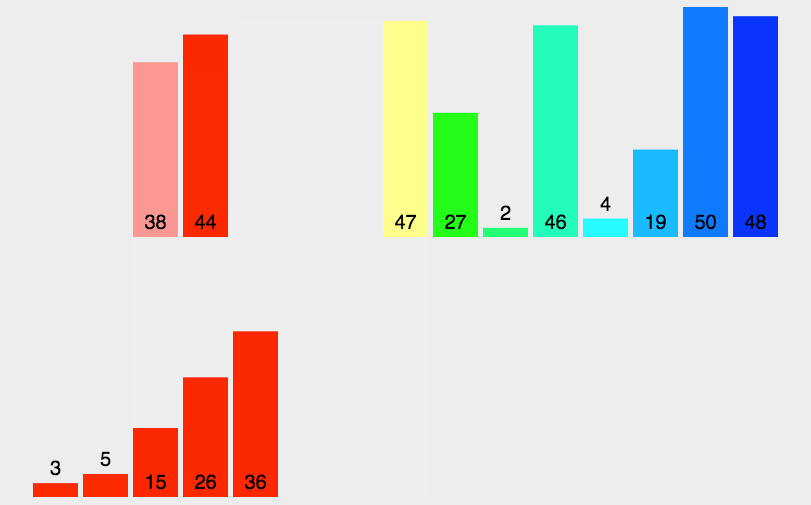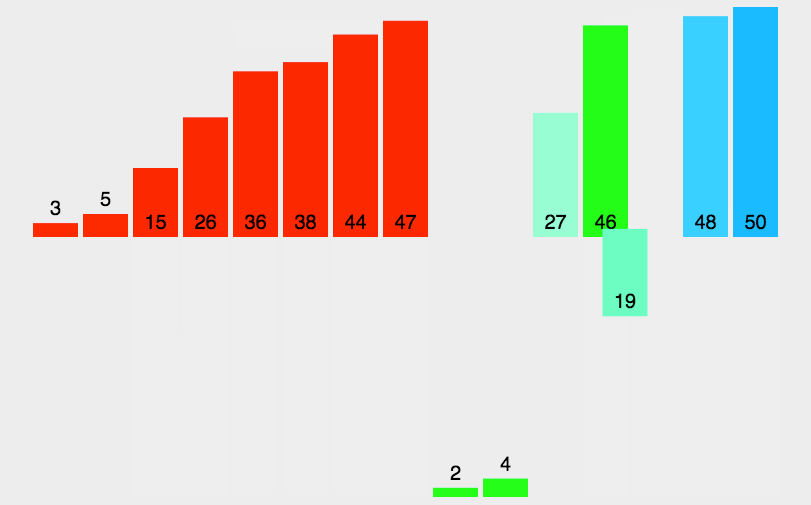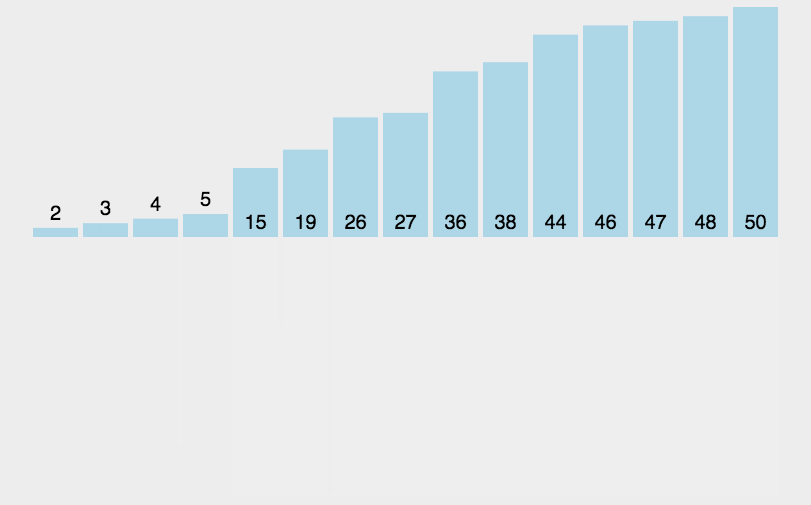
算法思想

简单来说，归并排序就是将一个数组排序的问题，可以先（递归得）将它分成两半分别排序，然后将结果归并起来。
归并：
将两个不同的有序数组合并到第三个数组中。

原地归并：

定义一个方法，merge(a,lo,mid,hi),它会将子数组a[lo…mid]和a[mid+1…hi]归并为一个有序的数组并将结果存放在原数组a[lo…hi]中。

//    原地归并的抽象方法
    public static void merge(Comparable[] a,int lo,int mid,int hi){

        //将a[lo..mid]和 a[mid+1..hi]归并
        int i=lo,j=mid+1;

        for (int k = lo; k <=hi; k++) {
            //将a[lo..hi]复制到aux[lo..hi]
            aux[k]=a[k];
        }
        for (int k = lo; k <=hi; k++) {
            //归并回到a[lo..hi]
            if(i>mid)                a[k]=aux[j++];
            else if(j>hi)            a[k]=aux[i++];
            else if(less(a[j],a[i])) a[k]=aux[j++];
            else                     a[k]=aux[i++];

        }
    }

方法实现时，先将所有元素复制到辅助数组aux[]中，然后再归并回a[]中。方法在归并时（第二个for循环）进行了4个判断：左半边用尽（取右半边的元素）、右半边用尽（取左半边的元素）、右半边的当前元素小于左半边的当前元素（取右半边的元素）、右半边的当前元素大于等于左半边的当前元素（取左半边的元素）.

自顶向下的归并排序

使用算法中的分治思想，也就是大事化小，小事化了的方式，将原来大数组的排序问题，不断切分为各个小的子数组的排序问题，最后将各个子数组的排序结果进行归并，解决原有大型数组排序问题。

自底向上的归并排序

与上面的思想相反，自底向上的归并是起始时将每个元素看成一个子数组，子数组依次两两合并，从部分到整体，最终解决原有大型数组排序问题。

算法实现（JAVA）

/**
 * @author zhangjinglong
 * @date 2019-06-20-23:04
 * 归并排序
 */

public class Merge {
    private static Comparable[] aux;//归并所需要的辅助数组

//    原地归并的抽象方法
    public static void merge(Comparable[] a,int lo,int mid,int hi){

        //将a[lo..mid]和 a[mid+1..hi]归并
        int i=lo,j=mid+1;

        for (int k = lo; k <=hi; k++) {
            //将a[lo..hi]复制到aux[lo..hi]
            aux[k]=a[k];
        }
        for (int k = lo; k <=hi; k++) {
            //归并回到a[lo..hi]
            if(i>mid)                a[k]=aux[j++];
            else if(j>hi)            a[k]=aux[i++];
            else if(less(a[j],a[i])) a[k]=aux[j++];
            else                     a[k]=aux[i++];

        }
    }


    //自顶向下的归并排序
    public static void sort(Comparable[] a){
        aux=new Comparable[a.length];//一次性分配空间
        sort(a,0,a.length-1);
    }
    private static void sort(Comparable[] a,int lo,int hi){
        //将数组a[lo..hi]排序
        if(hi<=lo) return;        //定义递归终止条件
        int mid=lo+(hi-lo)/2;
        sort(a,lo,mid);          //将左半边排序
        sort(a,mid+1,hi);    //将右半边排序
        merge(a,lo,mid,hi);      //归并结果

    }

    //这里给出自底向上的归并实现
    public static void sort2(Comparable[] a){
        //进行lgN次两两归并
        int N=a.length;
        aux=new Comparable[N];
        for(int zs=1;zs<N;zs=zs+zs)  //zs子数组大小
            for(int lo=0;lo<N-zs;lo+=zs+zs)  //lo:子数组索引
                merge(a,lo,lo+zs-1,Math.min(lo+zs+zs-1,N-1));
     }


    private static boolean less(Comparable v,Comparable w){
        return v.compareTo(w)<0;//升序
    }
    private static void exch(Comparable[] a,int i,int j){
        //交换数组中的两个元素
        Comparable t=a[i];
        a[i]=a[j];
        a[j]=t;
    }

    private static void show(Comparable[] a){
        //在单行中打印数组
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i]+"  ");
        }
        System.out.println();
    }
    public static boolean isSorted(Comparable[] a){
        //测试数组元素是否有序
        for (int i = 1; i < a.length; i++) {
            if(less(a[i],a[i-1])) return false;//如果数组中有相邻的任意两个元素逆序，则返回false
        }
        return true;
    }

    public static void main(String[] args) {
        String[] s={"I","A","B","Z","C","F"};
//        sort(s);
        assert isSorted(s);//用于检验我们的排序算法是否正常运行
        show(s);

    }


}