强连通分量及缩点tarjan算法解析@

强连通定义：在有向图G<V,E>中，对于点集V'∈V, 点集中的任意两点都可达，则称V'为强连通。

 

孤立的一个点也是一个强连通分量

 

在嵌套的多个环时 : {所有环上的点}为一个强连通分量( 最小环就是每个孤立点）注意一定是满足条件的最大点集。

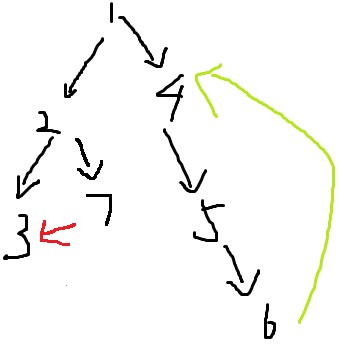
 则上图中强连通分量有 {1},{2},{3},{7},{4,5,6}

---------------------------------------------------------------------------

tarjan的过程就是dfs过程

对图dfs一下，遍历所有未遍历过的点 ，会得到一个有向树，显然有向树是没有环的。（注意搜过的点不会再搜）

则能产生环的 只有（指向已经遍历过的点）的边

如左图，只有红色与绿色边有可能产生环。

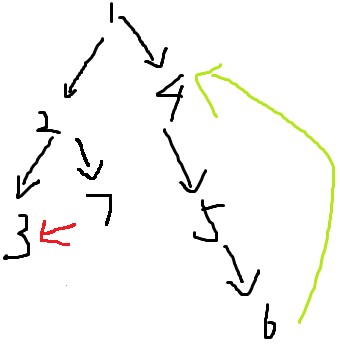
对于深搜过程，我们需要一个栈来保存当前所在路径上的所有点（栈中所有点一定是有父子关系的）

再仔细观察红边与绿边，首先得到结论：红边不产生环，绿边产生环

1、对于红边，连接的两个点3、7没有父子关系，这种边称为横叉边。

横叉边一定不产生环。

2、对于绿边，连接的两个点6、4是父子关系，这种边称为后向边。

环一定由后向边产生。

3、图中除了黑色的树枝边，一定只有横叉边和后向边（不存在其他种类的边）

-------------------------------------------------------------------------

则以下考虑对于这两种边的处理和判断：

首先深搜会搜到这样的图：

Stack = {1,2,3},3没有多余的其他边，因此3退栈，把3作为一个强连通分量

-------------------------------------------------------------------------

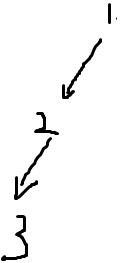
再次深搜：

此时栈 Stack = {1,2,7}

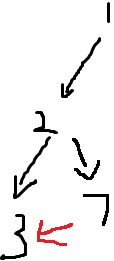
发现红边指向了已经遍历过的点3 => 是上述的2种边之一

而3不在栈中 => 3点与7点无父子关系

=> 该边为横叉边

=>采取无视法。

继而7点退栈 产生连通分量{7}

继而2点退栈 产生连通分量{2}

--------------------------------------------------------------------------------------

再次深搜：

此时 Stack = {1,4,5,6}

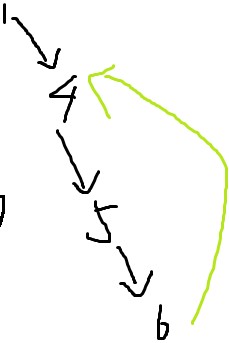
发现绿边指向了已经遍历过的点4 => 是上述的2种边之一

而4在栈中 => 4点与6点是父子关系

=> 该边为后向边

=>4->6的路径上的点都是环。

int num[N], Top = 0;
int u = Stack.top(); 
while(u!=4){ num[Top++] = u; Stack.pop(); u = Stack.top();}
num[Top++] = u;

如此就能把Stack中 4->6路径上的点转移到num数组里

显然num数组中的点是一个连通分量。

-------------------------------------------------------------------------

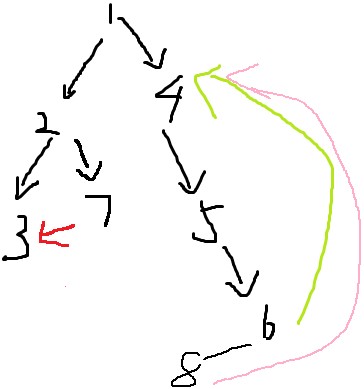
实际情况可能更复杂：

出现了大环套小环的情况，显然我们认为最大环是一个强连通分量(即:{4,5,6,8} ）

因而我们需要强化一下dfs过程：

定义：

int Time, DFN[N], Low[N];

DFN[i]表示 遍历到 i 点时是第几次dfs

Low[u] 表示 以u点为父节点的 子树 能连接到 [栈中] 最上端的点 的DFN值(换句话说，是最小的DFN，因为最上端的DFN是最小的嘛）

 

int Stack[N], top; //上述的栈

具体过程详见模版。

1. void add(int u, int v)  
2. {  
3.     edge[edgenum].from = u;  
4.     edge[edgenum].to = v;  
5.     edge[edgenum].nex = head[u];  
6.     head[u] = edgenum++;  
7. }  
8.   
9. void tarjan(int u)  
10. {  
11.     DFN[u] = low[u] = time++;  
12.     vis[u] = 1;  
13.     stack[top++] = u;  
14.     for(int i = head[u];i!=-1;i = edge[i].nex)  
15.     {  
16.         int v = edge[i].to;  
17.         if(DFN[v] == -1)  
18.         {  
19.             tarjan(v);  
20.             low[u] = min(low[u], low[v]);  
21.         }  
22.         else if(vis[v])  
23.         low[u] = min(low[u], DFN[v]);  
24.     }  
25.     if(DFN[u] == low[u])  
26.     {  
27.         taj++;  
28.         while(1)  
29.         {  
30.             int now = stack[--top];  
31.             vis[now] = 0;  
32.             belong[now] = taj;  
33.             if(now == u)  
34.             break;  
35.         }  
36.     }  
37. }  
38.   
39. void init()  
40. {  
41.     memset(head, -1, sizeof(head));  
42.     memset(DFN, -1, sizeof(DFN));  
43.     memset(low, -1, sizeof(low));  
44.     memset(vis, 0, sizeof(vis));  
45.     top = 0, taj = 0, time = 0;  
46.     edgenum = 0;  
47. }