QDU no cer的一道简单签到题(线性递推)

描述

人见人（不）爱，花见花（不）开的nr4强者Cerberux回来啦！

他不仅回来了，还带回来了一块2*n的长板。

然而他的蜜汁审美告诉他，这块长板需要贴瓷砖。

但是nr4强者Cerberux只有两种瓷砖，一种是1*2的，一种是1*1的。

他面对这块长板，突然脑抽了，想知道有多少种不同的用1*2和1*1瓷砖填满长板的方案。

大家都知道，nr4强者Cerberux不是一天炼成的。

他为了成为nr4强者，不仅舍弃了上课，拥抱了挂科，还离开了挚爱（个屁）的ACM。

所以他怎么可能会自己动脑想这个和魔方无关的问题。

于是nr4强者Cerberux想问你们有多少种填满长板的方案数？

如果你们回答出来了，将会免费获得由nr4强者Cerberux亲自授课的装x课程1个月（他不给不关我事）。

不同的两种方案必定至少有一个位置填放的瓷砖种类不同或者1*2的瓷砖的方向不同。

输入

第一行一个整数t代表数据组数
每组数据包括一个整数n；
1<=t<=100000
1<=n<=100000

输出

每组数据输出方案数并对1000000007取模，每组数据占一行。

样例输入1  复制

2
2
3

样例输出1

7
22

思路：走错了好几次思路，拐了几圈才回来。其实就是一个递推式，下面开始解释。

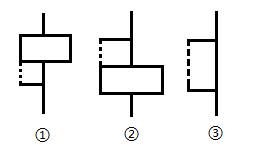
首先下面是每列的三个状态：

虚线代表不确定是不是一个小木块的边框，可以看到凸出来两个都是一个长木块导致的。

然后规定：每次不能在超过1列上进行开始插入木块。

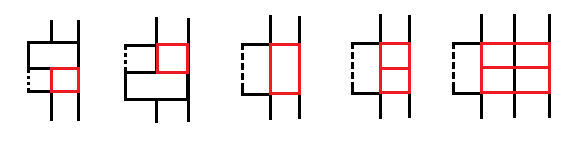
只推第i列的状态③和状态①的转移，进行解释。

首先是状态③的转移：

分别表示：从i-1的①转移，从i-1的②转移，从i-1的③转移方式1，从i-1的③转移方式2，从i-2的③转移。

再看状态②的转移：

分别表示：从i-1的②转移，从i-1的③转移。

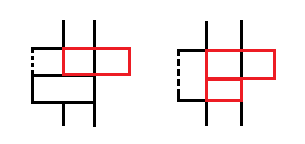
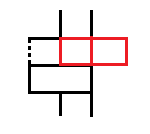
需要解释一下为什么不能跨两列插呢？假如对状态②转状态①时，我们进行这么的转移，

唯一的区别就是长木块被分为两个小木块了，但是不能这么进行转化。这么做相当于将②插一个小木块转化为下一列

的③之后再进行一次插小木块，就进行重复计算了。

Code1:

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 100000;
const int mod = 1000000007;
LL dp[maxn+5][5];
void init()
{
	dp[0][3] = 1; dp[1][3] = 2, dp[1][1] = 1, dp[1][2] = 1;
	for(int i = 2; i <= maxn; ++i)
	{
		dp[i][1] = (dp[i-1][2]+dp[i-1][3])%mod;
		dp[i][2] = (dp[i-1][1]+dp[i-1][3])%mod;
		dp[i][3] = (dp[i-1][2]+dp[i-1][1]+dp[i-1][3]*2+dp[i-2][3])%mod;
	}
}
int main()
{
	int t, n; init();
	scanf("%d", &t);
	while(t--)
	{
		scanf("%d", &n);
		printf("%lld\n", dp[n][3]);
	}
	return 0;
}

Code2(矩阵快速幂):

#include <algorithm>
#include <string.h>
#include <cstdio>  
#define LL long long  
using namespace std;  
const LL mod = 1e9+7;
const int maxn = 100000;
struct node
{
	LL m[4][4];
};
node multi(node x, node y)
{
	node res = {0, 0, 0, 0,
				0, 0, 0, 0,
				0, 0, 0, 0,
				0, 0, 0, 0};
	for(int i = 0; i < 4; ++i)
	for(int j = 0; j < 4; ++j)
	for(int k = 0; k < 4; ++k)
		res.m[i][j] += x.m[i][k]*y.m[k][j], res.m[i][j] %= mod;
	return res;
}
LL qpow(LL n)
{
	node ans = {1, 0, 0, 0, 
				0, 1, 0, 0,
				0, 0, 1, 0,
				0, 0, 0, 1};
	node bas = {0, 1, 1, 0,
				1, 0, 1, 0,
				1, 1, 2, 1,
				0, 0, 1, 0};
	node col = {1, 0, 0, 0,
				1, 0, 0, 0, 
				2, 0, 0, 0,
				1, 0, 0, 0};
	while(n)
	{
		if(n&1) ans = multi(ans, bas);
		bas = multi(bas, bas);
		n >>= 1;
	}
	return multi(ans, col).m[2][0];
} 
int main()  
{  
    int t, n;
    scanf("%d", &t);  
    while(t--)  
    {  
        scanf("%d", &n);  
        if(n == 1) {puts("2"); continue;}
		printf("%lld\n", qpow(n-1)); 
    }  
    return 0;  
} 

Code3(线性递推模板)：

#include <assert.h>
#include <vector>
#include <cstdio>
#define rep(i, a, n) for(int i = a; i < n; ++i)
#define per(i, a, n) for(int i = n-1; i >= a; --i)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(), (x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
using namespace std;
typedef vector<int> VI;
typedef long long ll;
typedef pair<int, int> PII;
const ll mod = 1000000007;

ll powmod(ll a, ll b)
{
	ll res = 1; a %= mod; 
	assert(b >= 0); 
	for(; b; b>>=1)
	{
		if(b&1) res = res*a%mod;
		a = a*a%mod;
	}
	return res;
}
int _;
ll n;
namespace linear_seq
{
    const int N = 10010;
    ll res[N], base[N], _c[N], _md[N];
    vector<int> Md;
    void mul(ll *a, ll *b, int k)
    {
        rep(i, 0, k+k) _c[i]=0;
        rep(i, 0, k) 
        	if(a[i]) rep(j,0,k) 
        		_c[i+j] = (_c[i+j] + a[i]*b[j])%mod;
        for(int i = k+k-1; i >= k; --i) 
        	if(_c[i]) rep(j,0,SZ(Md)) 
            	_c[i-k+Md[j]] = (_c[i-k+Md[j]] - _c[i]*_md[Md[j]])%mod;
        rep(i, 0, k) a[i] = _c[i];
    }
    int solve(ll n, VI a, VI b)
    {
        ll ans = 0, pnt = 0;
        int k = SZ(a);
        assert(SZ(a) == SZ(b));
        rep(i,0,k) _md[k-1-i] = -a[i];
        _md[k] = 1; Md.clear();
        rep(i, 0, k) if (_md[i] != 0) Md.push_back(i);
        rep(i, 0, k) res[i] = base[i] = 0;
        res[0] = 1;
        while((1ll<<pnt) <= n) ++pnt;
        for(int p = pnt; p >= 0; --p)
        {
            mul(res, res, k);
            if((n>>p) & 1)
            {
                for(int i = k-1; i >= 0; --i) res[i+1] = res[i];
                res[0] = 0;
                rep(j, 0, SZ(Md)) 
                res[Md[j]] = (res[Md[j]] - res[k]*_md[Md[j]])%mod;
            }
        }
        rep(i, 0, k) ans = (ans + res[i]*b[i])%mod;
        if(ans < 0) ans += mod;
        return ans;
    }
    VI BM(VI s)
    {
        VI C(1, 1), B(1, 1);
        int L = 0, m = 1, b = 1;
        rep(n, 0, SZ(s))
        {
            ll d = 0;
            rep(i, 0, L+1) d = (d + (ll)C[i]*s[n-i])%mod;
            if(d == 0) ++m;
            else if(2*L <= n) 
            {
                VI T = C;
                ll c = mod - d*powmod(b, mod-2)%mod;
                while(SZ(C) < SZ(B)+m) C.pb(0);
                rep(i, 0, SZ(B)) C[i+m] = (C[i+m] + c*B[i])%mod;
                L = n+1-L; B = T; b = d; m = 1;
            }
            else
            {
                ll c = mod - d*powmod(b, mod-2)%mod;
                while(SZ(C) < SZ(B)+m) C.pb(0);
                rep(i, 0, SZ(B)) C[i+m] = (C[i+m]+c*B[i])%mod;
                ++m;
            }
        }
        return C;
    }
    int gao(VI a, ll n)
    {
        VI c = BM(a);
        c.erase(c.begin());
        rep(i, 0, SZ(c)) c[i] = (mod-c[i])%mod;
        return solve(n, c, VI(a.begin(), a.begin()+SZ(c)) );
    }
};
int main()
{
	int T; scanf("%d", &T);
    while(T--)
    {
    	scanf("%lld", &n);
        printf("%lld\n", linear_seq::gao(VI{2,7,22,71,228,733}, n-1));
    }
    return 0;
}

继续加油~