题意:
对于所有x满足式子f(cos(x)) = cos(n*x);让我们求x关于函数f(x)的展开式x^m的系数,答案对998244353取模。
思路:
根据cos(n*x)式子我们可以化为若干个t*cos^k(x)的组合。例如n=2时,cos(2x) = -1+2cos^2(x)。
然后根据切比雪夫多项式,即论文中论述的。
可得到通项:
然后可根据其推理过程,简化求解方式:
所以综上,当n<k或者n和k的奇偶性不同时,我们直接特判为0。再发现m等于0的时候需要特殊处理一下,因为此时下面(n-k)!!的位数是比上面(n+k-2)!!的位数要多的,所以此时,我们要把多出来的这一点处理出来,在之后去求逆元。其它情况下面去抵消上面的若干位再求就行。(其实不特殊处理直接会导致过不了样例,但你能AC掉这题,数据太水= =)
代码:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod = 998244353;
int n, m;
ll a, b;
ll qpow(ll bas, ll n)
{
ll ans = 1;
while(n)
{
if(n&1) ans = ans*bas%mod;
bas = bas*bas%mod;
n >>= 1;
}
return ans;
}
int main()
{
while(~scanf("%d %d", &n, &m))
{
if(((n^m)&1) || n < m)
{
puts("0");
continue;
}
int key = (n-m)/2%2? -1: 1;
a = 1, b = 1;
for(int i = 1; i <= m; ++i)
b = b*i%mod;
if(m == 0) b = b*n%mod;
else
{
for(int i = n-m+2; i <= n+m-2; i+=2)
a = a*i%mod;
}
ll ans = a*qpow(b, mod-2)%mod*n%mod*key;
printf("%lld\n", (ans+mod)%mod);
}
return 0;
}
继续加油~










 本文介绍了一种利用切比雪夫多项式求解函数f(cos(x))=cos(nx)中x^m系数的方法,并给出了具体的实现思路与代码。通过对cos(nx)的表达式进行转换并结合切比雪夫多项式的性质,可以高效地计算出所求系数。
本文介绍了一种利用切比雪夫多项式求解函数f(cos(x))=cos(nx)中x^m系数的方法,并给出了具体的实现思路与代码。通过对cos(nx)的表达式进行转换并结合切比雪夫多项式的性质,可以高效地计算出所求系数。
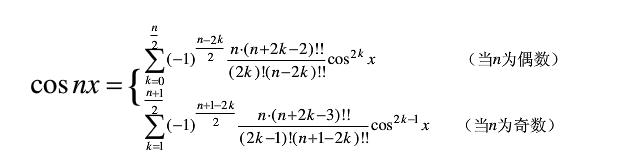

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








