最近在看网络编码的卷积网络编码部分,然后被幂级数环,有理幂级数环,形式幂级数弄昏头了。
1.幂级数:
幂级数是函数项级数中最基本的一类。它的特点是在其收敛区间绝对收敛,且幂级数在收敛区间内可逐项微分和积分。
幂级数的形式为:

1)收敛性
如果级数


如果级数


对于幂级数
若在

若在

推论:
如果幂级数
* 当
* 当
u*当
正数通常称R作幂级数的收敛半径。
2)幂级数的运算
加减法:
设幂级数





乘法:
除法:
2.形式幂级数
1)介绍
形式幂级数和多项式的形式定义有类似之处。可以看做也是不讨论幂级数敛散性,也就是将其中的不定元仅仅看作是一个代数对象,而不是任何具体数值的时候写出的幂级数。
比如说系数为阶乘的形式幂级数:![[1,1,2,6,24,120,, \cdots]](http://upload.wikimedia.org/math/e/3/7/e37a36d7f6a6850cbd613652fb4a1515.png) ,即使说它对应的幂级数:
,即使说它对应的幂级数:
在 取任何的非零实数值时都不收敛,我们仍然可以将其作为形式幂级数进行运算。
取任何的非零实数值时都不收敛,我们仍然可以将其作为形式幂级数进行运算。
和多项式环中的元素一样,形式幂级数之间也可以做加减和乘法的运算,具体的计算方式和多项式环一样。比如说设:
那么 与
与 的和就是:
的和就是:
其中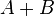 里面
里面 的系数就是
的系数就是 与
与 中
中 的系数的和;
的系数的和; 里面
里面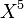 的系数就是
的系数就是 与
与 中
中 的阶数相加等于5的项的系数乘积的和:
的阶数相加等于5的项的系数乘积的和:
形式幂级数不仅能够定义乘法,也能定义乘法逆的运算。一个形式幂级数 的逆是指另一个形式幂级数
的逆是指另一个形式幂级数 ,使得
,使得 . 如果这样的形式幂级数
. 如果这样的形式幂级数 存在,就是唯一的,将其记为
存在,就是唯一的,将其记为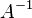 。同时我们也可以定义形式幂级数的除法:当
。同时我们也可以定义形式幂级数的除法:当 的逆存在时,
的逆存在时,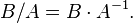
形式幂级数上的一个重要映射是系数的提取操作:将一个形式幂级数映射到它的 的系数。这个操作常常记作
的系数。这个操作常常记作![[X^n]](http://upload.wikimedia.org/math/d/2/2/d22347a90fa204de1cffe306f336db8f.png) ,比如说对形式幂级数
,比如说对形式幂级数 ,就有:
,就有:
 ,也有:
,也有:
![[X^3]B = 4](http://upload.wikimedia.org/math/3/f/7/3f7b440d99e72050825c97e0d0e66843.png) 。又比如:
。又比如:
![[X^2] ( X + 3 X^2 Y^3 + 10 Y^6) = 3 Y^3](http://upload.wikimedia.org/math/b/0/b/b0b2eed2db605ade897e5d73639b583e.png) ,
,
![[X^2 Y^3] ( X + 3 X^2 Y^3 + 10 Y^6) = 3](http://upload.wikimedia.org/math/6/e/1/6e18c043f99eb775bfed5932c87ec546.png) 。提取映射和多项式环中的对应映射一样,都可以看做是到一个子空间的投影映射。
。提取映射和多项式环中的对应映射一样,都可以看做是到一个子空间的投影映射。
2)形式幂级数的环结构
所有的不定元为 ,系数为某一个交换环
,系数为某一个交换环 上元素的形式幂级数构成一个环,称为
上元素的形式幂级数构成一个环,称为 上变量为
上变量为 的形式幂级数环,记作
的形式幂级数环,记作![R[[X]]](http://upload.wikimedia.org/math/1/e/d/1edaaf4a82237b5d111baaec4357d25c.png) 。
。
环结构:
首先可以定义集合![R[[X]]](http://upload.wikimedia.org/math/1/e/d/1edaaf4a82237b5d111baaec4357d25c.png) 的范围。作为一个集合,
的范围。作为一个集合,![R[[X]]](http://upload.wikimedia.org/math/1/e/d/1edaaf4a82237b5d111baaec4357d25c.png) 可以用和
可以用和 一样的方法构造。
一样的方法构造。 是所有
是所有 上元素构成的数列
上元素构成的数列 的集合:
的集合:
 中的元素可以定义加法和乘法:
中的元素可以定义加法和乘法:
其中乘法的定义方法也叫做求两个数列的系数的柯西乘积,也是一种卷积。可以证明,在以上的定义下, 是一个交换环。环的加法零元是
是一个交换环。环的加法零元是 ,乘法幺元是
,乘法幺元是 。于是我们可以将
。于是我们可以将 中的元素嵌入到
中的元素嵌入到 之中,
之中,
并将 映射到不定元
映射到不定元 ,这样通过以上定义的加法和乘法就可以将
,这样通过以上定义的加法和乘法就可以将 中的有限非零元元素同构为:
中的有限非零元元素同构为:
这样的结构和多项式环是一样的。所以对于更一般的 中元素
中元素 ,就可以自然地希望将其对应到
,就可以自然地希望将其对应到 :
:
但这个对应方式并不能通过有限项的加法和乘法得到,所以需要用一个约定上的映射![\varphi : \, R^{\mathbb{N}} \rightarrow R[[X]]](http://upload.wikimedia.org/math/b/1/2/b1279f74b472a371474add1998dc6317.png) 来做到:
来做到:
这个映射涵盖了之前的多项式的定义,并且可以定义
以及
这个定义使得 是一个同态,所以
是一个同态,所以![R[[X]]](http://upload.wikimedia.org/math/1/e/d/1edaaf4a82237b5d111baaec4357d25c.png) 也是一个交换环。
也是一个交换环。
在域F上的幂级数环一般记为F[[X]],形如












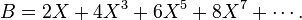
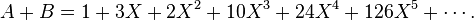
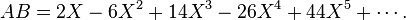
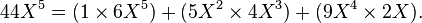
![[X^5]A = -11](http://upload.wikimedia.org/math/1/4/6/146854d71cda4237c446e18e393a19ab.png)
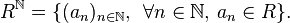
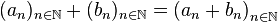


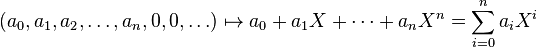
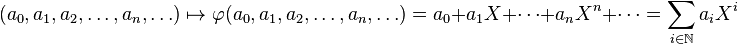
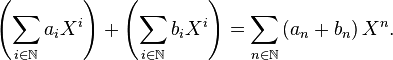















 9万+
9万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








