四阶龙格库塔法
这里主要讲一下如何用C语言编程运用四阶龙格库塔法求解微分方程组。对于所举例子,只是为了说明龙格库塔法不仅可以解一阶线性微分方程,高阶非线性也可通过降阶后按照经典四阶龙格库塔法公式逐步求解。只要选取合适的步长h,就能够平衡速度和精度,达到求解要求。至于例子中的一级倒立摆的物理含义没有提及到,各种方程具体是如何来的也没有涉及到推导。关于控制理论方面的知识这里不作重点。
对微分方程:dy/dt = f(x, y)
有初值条件:y(x(i))= φ(x(i))
y(i+1) = y(i)+h*(K1+2*K2+2*K3+K4)/6
K1=f(x(i),y(i))
K2=f(x(i)+h/2,y(i)+h*K1/2)
K3=f(x(i)+h/2,y(i)+h*K2/2)
K4=f(x(i)+h,y(i)+h*K3)
其中,K1, K2, K3, K4表示的是输出变量的一阶倒数,即在一点处的微分,斜率。
示例
以下以一个直线一级倒立摆为例。
根据牛顿经典力学可以建立以下二阶非线性微分方程组模型:
其状态方程为:
其输出方程为:
由微分方程可知,是一个高阶微分方程,先对其进行降阶:
令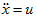
编程
不管是C语言编程还是Matlab编程,都只需根据公式和所要求解的具体微分方程来求解各斜率,循环4次,最终求解输出变量。
for(i = 0;i < 4;i++)
{
//直接写出所要求解的微分方程
dX[0] = x2;
dX[1] = u;
dX[2] = x4;
dX[3] = (3*u*cos(x3))+(29.4*sin(x3))-(0.165*(x4));
//将倒数即斜率赋值给k
k[0][i] = DX[0];
k[1][i] = DX[1];
k[2][i] = DX[2];
k[3][i] = DX[3];
//计算出x的值,供求下一组斜率k时使用
if(i==0||i==1)
{
x1 = X[0]+h*k[0][i]/2;
x2 = X[1]+h*k[1][i]/2;
x3 = X[2]+h*k[2][i]/2;
x4 = X[3]+h*k[3][i]/2;
}
if(i==2)
{
x1=X[0]+h*k[0][i];
x2=X[1]+h*k[1][i];
x3=X[2]+h*k[2][i];
x4=X[3]+h*k[3][i];
}
}
最终计算x值程序语句:
X[0] = X[0]+h*(k[0][0]+2*k[0][1]+2*k[0][3]+k[0][3])/6;
X[1] = X[1]+h*(k[1][0]+2*k[1][1]+2*k[1][3]+k[1][3])/6;
X[2] = X[2]+h*(k[2][0]+2*k[2][1]+2*k[2][3]+k[2][3])/6;
X[3] = X[3]+h*(k[3][0]+2*k[3][1]+2*k[3][3]+k[3][3])/6;







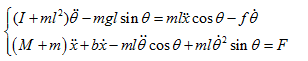
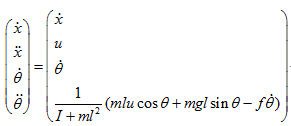
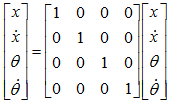
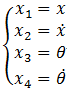














 1326
1326

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








