Description
Input
一共T+1行
第1行为数据组数T(T<=10)
第2~T+1行每行一个非负整数N,代表一组询问
Output
一共T行,每行两个用空格分隔的数ans1,ans2
Sample Input
6
1
2
8
13
30
2333
Sample Output
1 1
2 0
22 -2
58 -3
278 -3
1655470 2
分析
套路题。。复习一下罢了
代码
#include <bits/stdc++.h>
#define N 6050000
#define ll long long
ll phi[N + 5],mu[N + 5];
int tot;
int prime[N + 5];
bool notPrime[N + 5];
std::map <int,ll> mPhi,mMu;
void preWork()
{
mu[1] = phi[1] = 1;
for (int i = 2; i <= N; i++)
{
if (!notPrime[i])
{
prime[++tot] = i;
mu[i] = -1;
phi[i] = i - 1;
}
for (int j = 1; j <= tot && i * prime[j] < N; j++)
{
notPrime[i * prime[j]] = 1;
if (i % prime[j] == 0)
{
mu[i * prime[j]] = 0;
phi[i * prime[j]] = phi[i] * prime[j];
break;
}
mu[i * prime[j]] = -mu[i];
phi[i * prime[j]] = phi[i] * phi[prime[j]];
}
}
for (int i = 2; i <= N; i++)
phi[i] += phi[i - 1], mu[i] += mu[i - 1];
}
ll getPhiAns(ll x)
{
if (x <= N)
return phi[x];
if (mPhi.count(x))
return mPhi[x];
ll ans = (ll) x * (x + 1) / 2;
for (ll i = 2, last; i <= x; i++)
{
last = (x / (x / i));
ans -= (last - i + 1) * getPhiAns(x / i);
}
mPhi[x] = ans;
return ans;
}
ll getMuAns(ll x)
{
if (x <= N)
return mu[x];
if (mMu.count(x))
return mMu[x];
ll ans = (ll) x * (x - 1) / 2;
for (ll i = 2, last; i <= x; i++)
{
last = x / (x / i);
ans -= (last - i + 1) * getMuAns(x / i);
}
mMu[x] = ans;
return ans;
}
int main()
{
preWork();
int T;
scanf("%d",&T);
while (T--)
{
int n;
scanf("%d",&n);
printf("%lld ",getPhiAns(n));
printf("%lld\n",getMuAns(n));
}
}







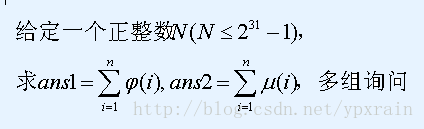
















 5042
5042

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








