线性回归的作用: 当我们获得数据之后, 我们想要知道这些数据间元素的关系, 我们可以定义一个等式去描述这中关系. 这就是线性回归的作用.
dependent variable: 就是要被预测的变量
Independent variable: 就是用来预测的变量
以下这个公式就是一个简单的线性回归的模型.
beta 0 和 1 都是模型的变量
epsilon 是随机变量, 作为error term. ( 个人理解: 因为现实生活中数据的预测结果可能被一些噪音所改变, 比如一个商店的销售额, 可能因为某天的某个客人很有钱而改变, 但是这种很有钱的客户很少见, 这种情况下的预测结果会有偏差, 使用epsilon 来进行校正. )

可能的线性回归图例:

线性回归的基本步骤:
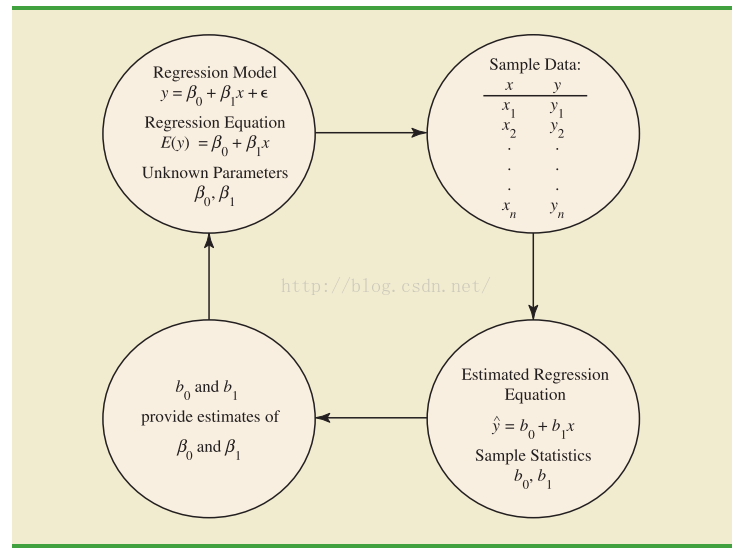
我们通过 regression model 的到 regression equation, 然后使用 历史数据 对regression equation 的参数进行优化 得到 estimated regression equation. 获得最优参数, 进行预测新的independent 数据
例子:
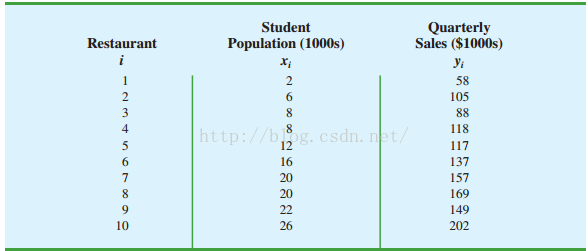
背景. 一连锁饭店的 销售额 和 坐落在它周围的 大学的 学生数量 可能有关系 所以我们对 销售额 和 学生数量 之间的关系很感兴趣.
我们收集了一部分历史数据. 如下
将数据转换为散点图:
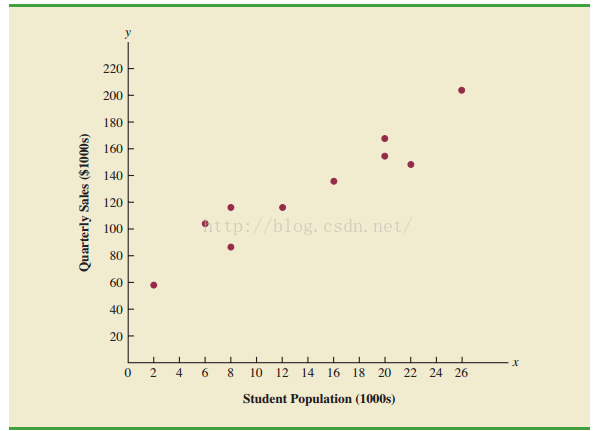
- 我们现在的问题 就能转化成 找到一条直线, 这条直线需要满足 使历史数据中的各个 x 所对应的 y 与 各个在直线上对应的y-head的差最小
- 公式 :
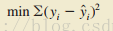 yi 是 历史数据x对应的y y-head 是 x 对应的在直线上y的值.
yi 是 历史数据x对应的y y-head 是 x 对应的在直线上y的值. - 根据estimation regression equation 我们知道
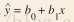
- 将 3 带入 2, 在对 b0 和 b1 分别求 偏导. 如图 (下图为错误版本,b1推导错误,感谢 qq_31442743 同学的指正, 正确版本 见 第 5 步)

 第二遍修改居然还修改错了,感谢同学再次指正。果然上完一天班脑子就是乱的。
第二遍修改居然还修改错了,感谢同学再次指正。果然上完一天班脑子就是乱的。
发现问题欢迎指出.谢谢





 线性回归用于揭示数据元素间的关系,通过定义等式描述这种关系。依赖变量是被预测的变量,独立变量是预测用的变量。线性回归模型包括随机变量epsilon以修正预测误差。基本步骤包括利用历史数据优化回归方程参数,找到使误差最小的直线。例如,饭店销售额可能与周围大学学生数量有关,通过线性回归找寻两者间的最佳拟合线。
线性回归用于揭示数据元素间的关系,通过定义等式描述这种关系。依赖变量是被预测的变量,独立变量是预测用的变量。线性回归模型包括随机变量epsilon以修正预测误差。基本步骤包括利用历史数据优化回归方程参数,找到使误差最小的直线。例如,饭店销售额可能与周围大学学生数量有关,通过线性回归找寻两者间的最佳拟合线。
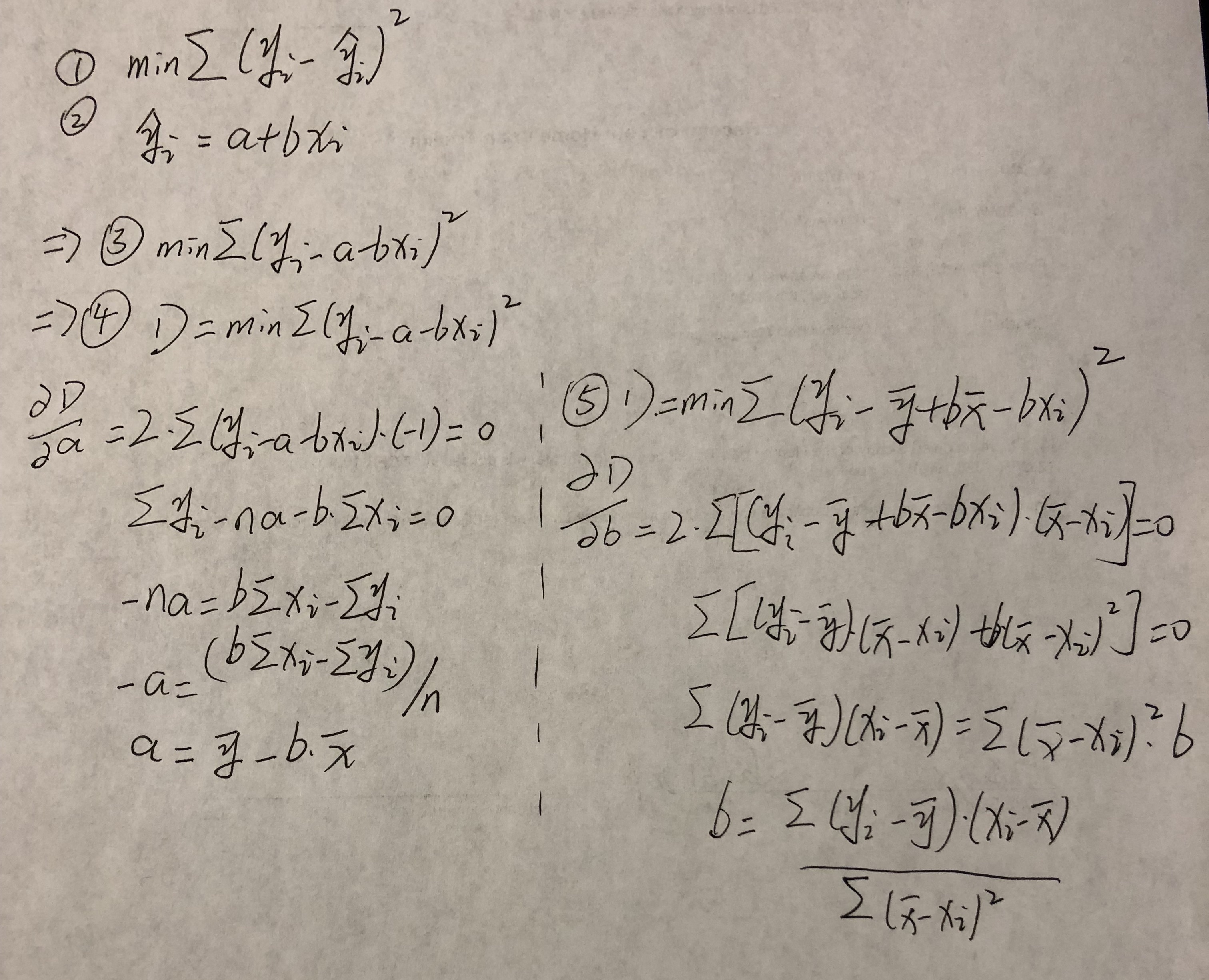
















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








