题意:要求求解出H,其中H%Mi=Ai ; 其中i=1,2,,,,,N;
样例说明:
T
N
M1,M2,,,,,Mn
A1,A2,,,,,,An
其实该题是要求我们解这样一个方程组:
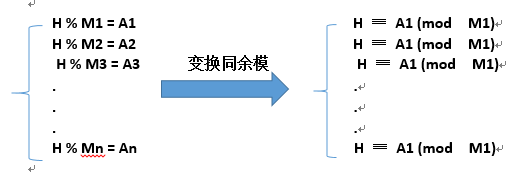
首先先介绍一下同于方程组的解发;
一:解二元一次非其次方程组
令方程组为: ax + by = c (1)
看到这式子我们首先要想到的就是欧几里得扩展原里,即若c为a与b的最大公约数,则可以利用欧几里得扩展原理求出x , y 的解,(至于欧几里得扩展原理该篇文章不讲述),但这里c不一定是a , b的最大公约数所以要解该方程还需要在原有的欧几里得扩展原理上修改一下。
我们令d=gcd(a,b),则可以通过欧几里得扩展原理求出 :
a * x1+b * y1=d (2)
若c%d=0 这(1)方程有解, 因为在(2)方程两边同时乘c/d 就可以得到(1)方程的解了。 所以有 x=x1*(c/d) y=x2*(c/d) 但是这只是该方程的一组解,
接下来求一下该方程的通解
令 (x,y) 是该方程的任意组解。 令由上面的方法我们可以求出方程的一组特解为(x1,y1),由方程(1)定义可知 :a * x+b * y = c 且 a * x1+b * y1 = c 所以 有 :
a * x+b * y = a * x1+b * y1 ;移项后可得 a * (x-x1)=b * (y1-y) (3) 由于d=gcd(a,b),所以a,b都能整除d ,令A=a/d B=b/d 所以有 A * (x-x1)= B* (y1-y) 且其中A与B互素 所以要想该式成立则 (x-x1) % B=0且(y1-y) % A=0 。所以 x=x1+k * B y=y1-k * A;(其中k为任意常数)
二:解同余模方程组
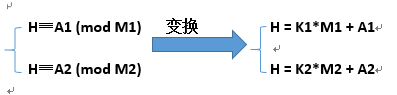
所以:K1*M1+A1 = K2*M2+A2 移项得到 K1*M1-K2*M2=A2-A1 。
再令a=M1,b=M2,c=(A2-A1) , x=K1,y=-K2 则该表达时可以表示为a*x+b*y=c, 而a,b,c为常数要求x,y。这时我们就可以用上面的方法来求解,先通过欧几里得扩展原理 求出特解(x1,y1) 然后通过通解公式求出: x=x1+k*B =x1+k*(b/d) (注意k可以为负数) 。这里还要求x是最小整数解,x=x%(b/d) ,然后将x带入原式的一式中。得到:
H=M1*(x1+k(b/d))+A1(k可以为任意实数) 变形得到 :
H=(M1*(b/d)*K+(M1*x1+A1)
若我们令M3=M1*(b/d) ,A3=M1*x1+A1 则可以得到新的一项H≡A3 (mod M3) 这样我们就将两项何为一项。只要我们这样一直做下去就可以将n项合为一项:
H≡An+1 (mod Mn+1) 即 H=k*Mn+1+An+1(最后一项)。
我们取k=0可得到H的 最小值为H=Mn+1。
注意:若An+1=0 则说明H刚好是M1,M2,,,,Mn的最小公倍数。
最后再讲一下同余模方程组的几个定理:
a ≡c(mod b)
其实方程等价于 a – y*b = c,即a%b=c(y为某一实数)。我们可以 统一的写成:
(欧几里得形式) a*x+b*y=c。
定理一:
设d = gcd(a, n), 假定对整数x’, y’, 有d = ax’ + ny’, 如果c%d=0,
则方程a ≡c(mod b)有一个解的值为x0, 满足:x0 = x’(b / d)(mod b)(b以内的解)
定理二:
假设方程a = c(mod b)有解, x0是方程的任意一个解, 则方程对模b恰有d个不同的解, 分别为: xi = x0 + i * (b / d), 其中 i = 1,2,3……d – 1 ( d=gcd(a,b) )
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
using namespace std;
int T,N;
int M[10],A[10];
int ex_gcd(int a,int b,int &x,int &y)
{//欧几里得扩展
if(b==0)
{
x=1; y=0;
return a;
}
int d=ex_gcd(b,a%b,y,x);
y=y-(a/b)*x;
return d;
}
int gcd(int a,int b)
{//欧几里得
while(b)
{
int t=a;
a=b;
b=t%b;
}
return a;
}
int solve()
{
int a,b,c,d,x,y,yu;
a=M[0];
yu=A[0];
for(int i=1;i<N;i++)
{//合并方程组
b=M[i];
c=A[i]-yu;
d=ex_gcd(a,b,x,y);
if(c%d)
return -1;
int B=b/d;
x=((c/d*x)%B+B)%B;
yu=x*a+yu;
a=a*B;
}
if(yu)
return yu;
else
{//最后余数为0的情况
int key=M[0];
for(int i=1;i<N;i++)
key=key*M[i]/gcd(key,M[i]);
return key;
}
}
int main()
{
scanf("%d",&T);
for(int i=1;i<=T;i++)
{
scanf("%d",&N);
for(int j=0;j<N;j++)
scanf("%d",&M[j]);
for(int j=0;j<N;j++)
scanf("%d",&A[j]);
printf("Case %d: %d\n",i,solve());
}
return 0;
}








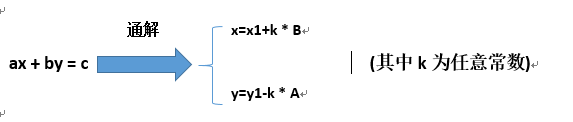














 680
680

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








