第二章 光网络链路
2.1 光网络链路结构
光纤通信网络如下图所示:Cable-有线电视,FTTH-光纤到户,。。。

光纤通信系统的组成(将传输按照系统/链路去看):
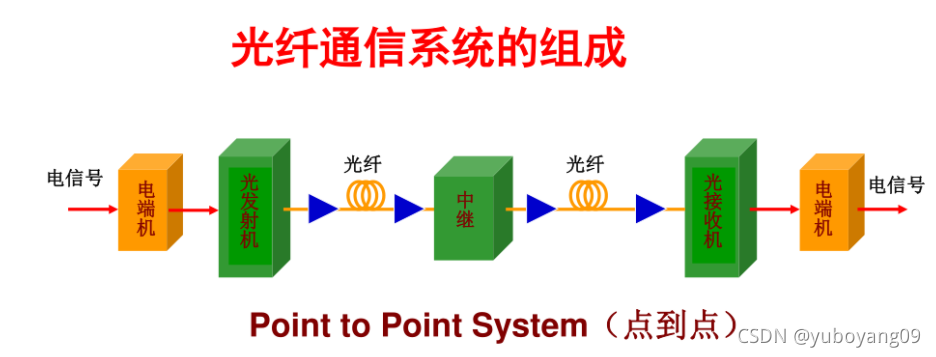
所谓点到点,就是一个通道中传输的通常是一个波长的传输信号

所谓波分复用系统,就是说,在一根光纤里面可以传输很多个不同波长的通道。可以看作点对点系统的集合。
2.2 光纤的类型与频谱资源
光纤结构 : 纤芯(Core)+包层(Cladding)+涂覆层

1. 光纤类型
光 纤 材 料 { 石 英 光 纤 掺 杂 光 纤 { 掺 铒 光 纤 掺 镨 光 纤 掺 氟 光 纤 掺 铥 光 纤 多 组 分 玻 璃 光 纤 塑 料 光 纤 光纤材料 \begin{cases} 石英光纤& \text{}\\ 掺杂光纤&\text{}\begin{cases}掺铒光纤&\text{}\\ 掺镨光纤&\text{}\\ 掺氟光纤&\text{}\\ 掺铥光纤&\text{}\\\end{cases} \\ 多组分玻璃光纤& \text{}\\ 塑料光纤& \text{}\\\end{cases} 光纤材料⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧石英光纤掺杂光纤多组分玻璃光纤塑料光纤⎩⎪⎪⎪⎨⎪⎪⎪⎧掺铒光纤掺镨光纤掺氟光纤掺铥光纤
折 射 率 分 布 { 阶 跃 型 光 纤 渐 变 型 光 纤 { 平 方 律 型 抛 物 线 型 中 心 凹 型 高 斯 型 三 角 型 多 层 光 纤 折射率分布 \begin{cases} 阶跃型光纤& \text{}\\ 渐变型光纤&\text{}\begin{cases}平方律型&\text{}\\ 抛物线型&\text{}\\ 中心凹型&\text{}\\ 高斯型&\text{}\\ 三角型&\text{}\\\end{cases} \\ 多层光纤& \text{}\\\end{cases} 折射率分布⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧阶跃型光纤渐变型光纤多层光纤⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧平方律型抛物线型中心凹型高斯型三角型

传 输 特 性 { 传 输 模 式 { 单 模 光 纤 多 模 光 纤 色 散 特 性 { 色 散 位 移 光 纤 非 零 色 散 光 纤 色 散 补 偿 光 纤 大 有 效 面 积 光 纤 偏 振 特 性 —保偏光纤 { 几 何 截 面 非 圆 对 称 { 椭 圆 光 纤 矩 形 光 纤 D 型 光 纤 折 射 率 剖 面 非 圆 对 称 { 熊 猫 光 纤 领 结 光 纤 损 耗 特 性 { 全 波 光 纤 低 损 耗 光 纤 非 线 性 特 性 —光子晶体光纤 传输特性 \begin{cases} 传输模式& \text{}\begin{cases} 单模光纤&\text{}\\ 多模光纤&\text{}\\ \end{cases} \\ 色散特性&\text{}\begin{cases}色散位移光纤&\text{}\\ 非零色散光纤&\text{}\\ 色散补偿光纤&\text{}\\ 大有效面积光纤&\text{}\\\end{cases} \\ 偏振特性& \text{---保偏光纤}\begin{cases} 几何截面非圆对称&\text{} \begin{cases} 椭圆光纤&\text{}\\ 矩形光纤&\text{}\\ D型光纤&\text{}\\ \end{cases} \\ 折射率剖面非圆对称&\text{} \begin{cases} 熊猫光纤&\text{}\\ 领结光纤&\text{}\\ \end{cases} \\ \end{cases} \\ 损耗特性& \text{}\begin{cases} 全波光纤&\text{}\\ 低损耗光纤&\text{}\\ \end{cases} \\ 非线性特性& \text{---光子晶体光纤}\\\end{cases} 传输特性⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧传输模式色散特性偏振特性损耗特性非线性特性{单模光纤多模光纤⎩⎪⎪⎪⎨⎪⎪⎪⎧色散位移光纤非零色散光纤色散补偿光纤大有效面积光纤—保偏光纤⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧几何截面非圆对称折射率剖面非圆对称⎩⎪⎨⎪⎧椭圆光纤矩形光纤D型光纤{熊猫光纤领结光纤{全波光纤低损耗光纤—光子晶体光纤
2. 光纤频谱资源

对于长途通信,可实用1280~1640nm波段 ——>带宽达370nm
若波分复用信道间隔为50GHz(~0.5nm) ——>可实现740个信道
若每个信道传输速率为10Gbit/s ——>可在单根光纤上传输7.4Tbit/s
若每个信道传输速率为40Gbit/s ——>可在单根光纤上传输29.6Tbit/s
2.3 光纤的损耗与全波光纤
1.光纤的损耗
引起光纤损耗的机制:吸收损耗、散射损耗、弯曲损耗
(1)衰减系数(损耗系数):光信号在光纤中传播时,其功率随距离L的增加呈指数衰弱
(
d
P
d
x
)
\left(\frac{dP}{dx}\right)
(dxdP) =-αP

(2)吸收损耗
· 本征吸收(SiO2):构成SiO2的离子晶格在光波(电磁波) 作用下发生振动损失的能量
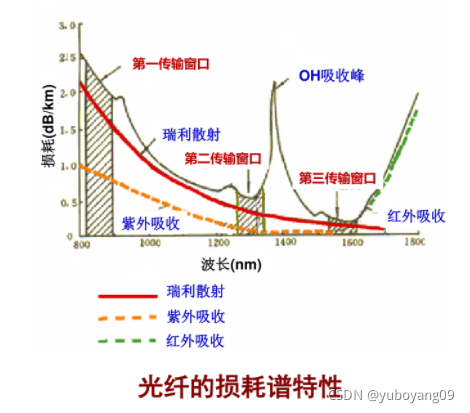
紫外吸收: 吸收峰值0.16 μm,
吸收带尾部拖到1μm
→ 影响 0.7μm~1μm波段的通信
红外吸收: 吸收峰值 9.1μm、12.5μm、21μm,
吸收带尾部拖到1.5μm~1.7μm
→ 通波段扩展的困难之一
· 杂质吸收
OH离子吸收: 吸收峰值1.39 μm 、1.24 μm 、0.95 μm
- 在峰之间的低损耗区,构成光纤通信的三个窗口
金属离子吸收: Cr、Mn、Fe等 产生边带吸收峰0.5 μm~1.1 μm
→ 通过改进工艺,其影响可以忽略不计
(3)散射损耗
· 瑞利散射 :瑞利散射损耗与波长的四次方成反比。


在制造过程中,材料密度不均匀 —> 折射率不均匀。
· 波导散射
纤芯直径沿轴向不均匀 —> 导模与辐射模之间的耦合
· 非线性散射
光功率增大到一定程度 —> 非线性受激拉曼散射和受激布里渊散射
(4)弯曲损耗
光纤的弯曲有两种形式:
· 宏弯(或弯曲): 曲率半径比光纤的直径大得多的弯曲
在光缆的生产、接续和施工过程中,不可避免地出现弯曲。 光纤有一定曲率半径的弯曲时就会产生辐射损耗。
当曲率半径减小时,损耗以指数形式增加。




弯曲半径减小,损耗指数增加
· 微弯:光纤轴线产生微米级的弯曲
由于光纤受到侧压力和套塑光纤遇到温度变化时,光纤的纤芯、 包层和套塑的热膨胀系数不一致而引起的。
其损耗机理和弯曲一致,也是由模式变换引起的。
微弯导致了导波模与泄漏模或非导波模之间的重复性能量耦合。
微弯的原因:
光纤的生产过程中带来的不均
成缆时受到压力不均
使用过程中由于光纤各个部分热胀冷缩的不同
导致的后果:
造成能量辐射损耗

2.全波光纤
全波光纤实测数据如下:

3.超低损耗光纤
普通光纤(G.652):衰减降低到0.18 dB/km后很难进一步降低。
原因:通过在纤芯中掺杂稀土元素锗来提高纤芯的折射率,从而和纯二氧化硅的包层材料间形成折射率差,以保证入射光在单模光纤中的传播。
但由于芯层中掺入GeO2等金属氧化物,而使瑞利散射损耗增加。因此掺锗光纤的衰减无法进一步降低。

纯SiO2单模光纤:由于在芯层中没有掺杂,减小了由于瑞利散射导致的衰减,实现了光纤损耗的进一步降低。

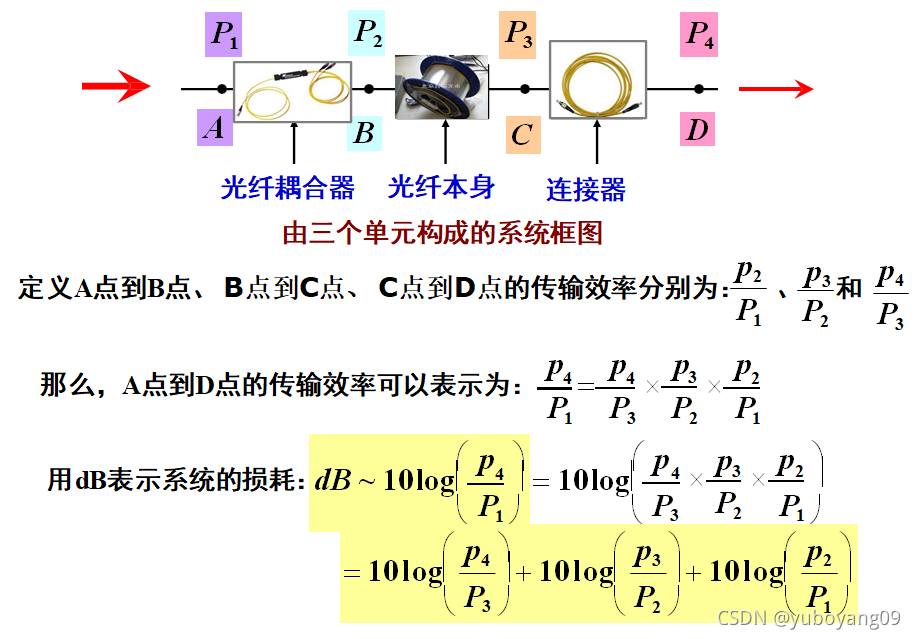
dB and dBm



2.4 光纤的色散与色散光纤
1.光纤的色散特性
· 什么是色散?
不同波长的光,在介质中传播,由于介质材料对应不同波长光波的折射率不同,从而使得光波的传播速度不同,最终导致不同波长的光波分离。
光纤中光信号的不同波长和不同模式成分,具有不同的传播速度,称为色散。
· 色散特性的描述
光
载
波
是
以
相
速
度
传
播
:
V
p
=
ω
β
光
信
息
是
以
群
速
度
(
调
制
包
络
的
速
度
)
传
播
:
V
g
=
d
ω
d
β
=
c
d
k
0
d
β
k
0
=
2
π
λ
假
设
频
率
为
ω
的
一
光
谱
分
量
经
过
长
为
L
的
光
纤
传
输
,
则
产
生
的
时
延
为
τ
=
L
v
g
由
于
光
脉
冲
包
含
许
多
频
率
分
量
,
所
以
不
同
频
率
分
量
的
光
在
传
输
后
产
生
不
同
的
延
迟
,
不
能
同
时
到
达
光
纤
输
出
端
,
从
而
导
致
了
脉
冲
的
展
宽
。
假
设
光
脉
冲
的
谱
宽
为
Δ
ω
,
则
脉
冲
展
宽
为
:
Δ
τ
=
d
τ
d
ω
Δ
ω
=
L
β
Δ
ω
其
中
,
β
2
=
d
1
v
g
d
ω
=
d
2
β
d
ω
2
,
称
为
群
速
度
色
散
,
直
接
决
定
了
脉
冲
在
光
纤
中
的
展
宽
程
度
。
光载波是以相速度传播:V_{p} ={\omega \over \beta }\\ 光信息是以群速度(调制包络的速度)传播: V_{g} ={ d\omega\over{d\beta} }= c{dk_{0}\over d\beta} \\k_0 ={2\pi\over\lambda} \\ 假设频率为\omega的一光谱分量经过长为L的光纤传输,则产生的时延为\tau = {L\over v_g} \\ 由于光脉冲包含许多频率分量,所以不同频率分量的光在传输后产生不同的延迟,不\\能同时到达光纤输出端,从而导致了脉冲的展宽。\\假设光脉冲的谱宽为\Delta\omega,则脉冲展宽为:\\ \Delta\tau = {d\tau\over d\omega}\Delta\omega = L\beta\Delta\omega\\ \\ 其中,\beta_2 = {d{1\over v_g}\over d\omega} = {d^2\beta\over d\omega^2 },\\ \\称为群速度色散,直接决定了脉冲在光纤中的展宽程度。
光载波是以相速度传播:Vp=βω 光信息是以群速度(调制包络的速度)传播:Vg=dβdω=cdβdk0k0=λ2π 假设频率为ω的一光谱分量经过长为L的光纤传输,则产生的时延为τ=vgL 由于光脉冲包含许多频率分量,所以不同频率分量的光在传输后产生不同的延迟,不能同时到达光纤输出端,从而导致了脉冲的展宽。假设光脉冲的谱宽为Δω,则脉冲展宽为: Δτ=dωdτΔω=LβΔω 其中,β2=dωdvg1=dω2d2β, 称为群速度色散,直接决定了脉冲在光纤中的展宽程度。
光
纤
通
信
系
统
中
,
Δ
ω
由
光
源
的
谱
宽
Δ
λ
决
定
,
常
用
Δ
λ
代
替
Δ
ω
,
ω
=
2
π
c
λ
-
>
Δ
ω
=
−
2
π
c
λ
2
Δ
λ
则
脉
冲
展
宽
为
:
Δ
τ
=
L
β
2
Δ
ω
=
−
2
π
c
λ
2
β
2
L
Δ
λ
=
D
L
Δ
λ
其
中
,
D
=
−
2
π
c
λ
2
β
2
=
−
2
π
c
λ
2
d
2
β
d
ω
2
,
称
为
色
散
系
数
,
单
位
:
p
s
/
(
n
m
⋅
k
m
)
表
示
:
光
源
光
谱
中
,
波
长
间
隔
为
1
n
m
的
光
波
,
传
输
1
k
m
后
,
由
于
色
散
效
应
产
生
的
时
延
差
。
注
:
标
准
单
模
光
纤
在
1550
n
m
处
的
色
散
系
数
约
为
17
p
s
/
n
m
⋅
k
m
光纤通信系统中,\Delta\omega由光源的谱宽\Delta\lambda决定,常用\Delta\lambda代替\Delta\omega ,\\ \\\omega = {2\pi c\over \lambda} ->\Delta\omega ={-2\pi c \over \lambda^2}\Delta\lambda\\ \\则脉冲展宽为:\Delta\tau =L\beta_2\Delta\omega=-{2\pi c\over \lambda^2}\beta_2L\Delta\lambda=DL\Delta\lambda\\ \\其中,D=-{2\pi c\over \lambda^2}\beta_2=-{2\pi c\over \lambda^2}{d^2\beta\over d\omega^2 },称为色散系数,单位:ps/(nm·km)\\ \\表示:光源光谱中,波长间隔为1nm的光波,传输1km后,由于色散效应产生的时延差。\\注:标准单模光纤在1550nm处的色散系数约为17ps/nm·km
光纤通信系统中,Δω由光源的谱宽Δλ决定,常用Δλ代替Δω, ω=λ2πc ->Δω=λ2−2πcΔλ 则脉冲展宽为:Δτ =Lβ2Δω=−λ22πcβ2LΔλ=DLΔλ 其中,D=−λ22πcβ2=−λ22πcdω2d2β,称为色散系数,单位:ps/(nm⋅km) 表示:光源光谱中,波长间隔为1nm的光波,传输1km后,由于色散效应产生的时延差。注:标准单模光纤在1550nm处的色散系数约为17ps/nm⋅km
正
色
散
,
负
色
散
和
零
色
散
色
散
系
数
D
,
群
色
散
速
度
β
2
(
1
)
D
>
0
:
负
色
散
β
2
<
0
:
v
g
高
频
光
>
v
g
低
频
光
(
2
)
D
<
0
:
正
色
散
β
2
>
0
:
v
g
高
频
光
<
v
g
低
频
光
(
3
)
D
=
0
:
零
色
散
正色散,负色散和零色散\\ 色散系数D,群色散速度\beta_2\\(1)D>0:负色散 \beta_2<0:v_{g高频光}>v_{g低频光}\\ (2)D<0:正色散 \beta_2>0:v_{g高频光}<v_{g低频光} \\(3)D=0:零色散
正色散,负色散和零色散 色散系数D,群色散速度β2(1)D>0:负色散 β2<0:vg高频光>vg低频光 (2)D<0:正色散 β2>0:vg高频光<vg低频光 (3)D=0:零色散
· Δ色散产生的原因
(1) 光源的非单色性
(2) 光信号是被调制了的波谱
(3) 传输光纤的色散
· 色散的影响
模
拟
信
号
的
幅
度
衰
减
一
>
探
测
功
率
降
低
一
>
信
噪
比
劣
化
数
字
信
号
脉
冲
展
宽
一
>
码
间
串
扰
一
>
增
加
误
码
率
}
限
制
通
信
容
量
和
传
输
距
离
\left. \begin{matrix} 模拟信号的幅度衰减一>探测功率降低一>信噪比劣化 \\ 数字信号脉冲展宽一>码间串扰一>增加误码率 \end{matrix} \right\}限制通信容量和传输距离
模拟信号的幅度衰减一>探测功率降低一>信噪比劣化数字信号脉冲展宽一>码间串扰一>增加误码率}限制通信容量和传输距离
· 光纤的传输带宽
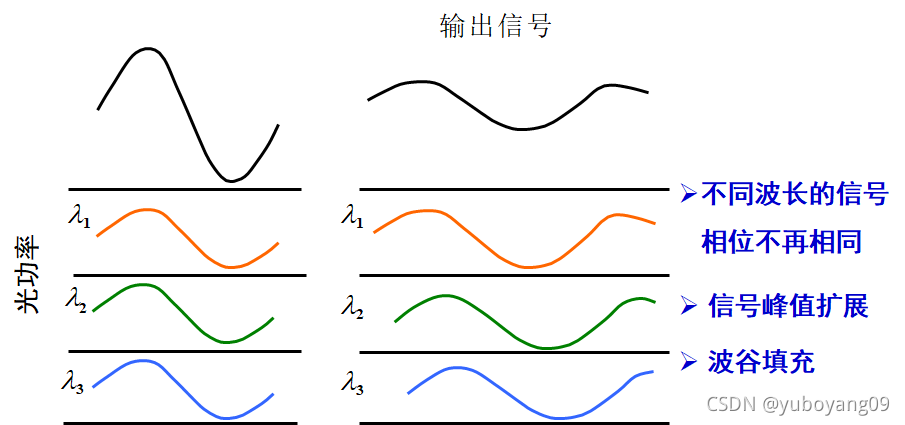
色散导致模拟信号的幅度衰弱
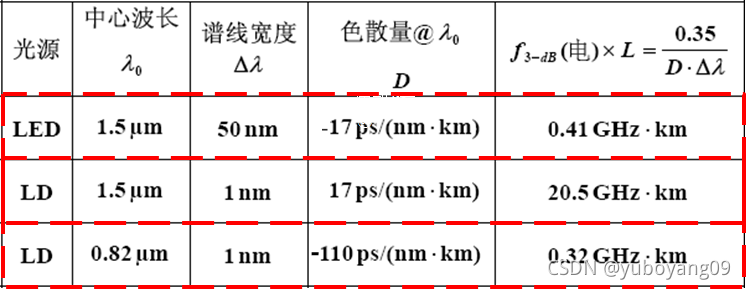
当 两 个 波 长 载 波 的 时 延 等 于 半 调 制 ( Δ τ = T 2 ) 周 期 时 , 调 制 被 完 全 抵 消 。 如 果 T / 2 是 系 统 最 大 的 可 接 受 时 延 , 也 就 是 延 时 间 隔 Δ τ < = T 2 , 那 么 调 制 频 率 f = 1 T < = 1 2 Δ τ , 该 表 达 式 所 决 定 的 ∗ ∗ 上 限 频 率 ∗ ∗ 是 系 统 3 − d B 带 宽 的 一 个 很 好 的 近 似 3 − d B 光 带 宽 为 : f 3 − d B ( 光 ) = 1 2 Δ τ , f 1.5 − d B ( 光 ) = 0.71 f 3 − d B ( 光 ) = f 3 − d B ( 电 ) 通 常 , 用 3 − d B 电 带 宽 表 示 系 统 带 宽 : f 3 − d B ( 电 ) = 0.35 Δ τ f 3 − d B ( 电 ) × L = 0.35 Δ ( τ / L ) = 0.35 D ⋅ Δ λ ⋅ ⋅ ⋅ ( 1 ) 单 位 : H z ⋅ k m , D 光 纤 的 色 散 系 数 , Δ λ 光 源 的 线 宽 公 式 ( 1 ) 通 常 用 来 衡 量 光 纤 的 通 信 容 量 当两个波长载波的时延等于半调制(\Delta\tau={T\over2})周期时,调制被完全抵消。\\ \\如果T/2是系统最大的可接受时延,也就是延时间隔\Delta\tau <= {T\over2},那么调制频率f = {1\over T}<={1\over 2\Delta\tau},该表达式所决定的\\ \\**上限频率**是系统3-dB带宽的一个很好的近似\\ \\ 3-dB光带宽为:f_{3-dB}(光) = {1\over2\Delta\tau}, f_{1.5-dB} (光)= 0.71f_{3-dB}(光)=f_{3-dB}(电)\\ \\ 通常,用3-dB电带宽表示系统带宽:\\ f_{3-dB}(电) = {0.35\over \Delta\tau}\\ \\ \\ f_{3-dB}(电) × L = {0.35\over \Delta(\tau/L)} = {0.35\over D·\Delta\lambda} ···(1)\\ \\ 单位:Hz·km,D光纤的色散系数,\Delta\lambda光源的线宽\\ 公式(1)通常用来衡量光纤的通信容量 当两个波长载波的时延等于半调制(Δτ=2T)周期时,调制被完全抵消。 如果T/2是系统最大的可接受时延,也就是延时间隔Δτ<=2T,那么调制频率f=T1<=2Δτ1,该表达式所决定的 ∗∗上限频率∗∗是系统3−dB带宽的一个很好的近似 3−dB光带宽为:f3−dB(光)=2Δτ1, f1.5−dB(光)=0.71f3−dB(光)=f3−dB(电) 通常,用3−dB电带宽表示系统带宽:f3−dB(电) = Δτ0.35 f3−dB(电)×L = Δ(τ/L)0.35=D⋅Δλ0.35 ⋅⋅⋅(1) 单位:Hz⋅km,D光纤的色散系数,Δλ光源的线宽公式(1)通常用来衡量光纤的通信容量
通信容量的例子:
 带
宽
限
制
=
带
宽
−
距
离
积
链
路
长
度
带宽限制={带宽 - 距离积\over 链路长度}\\
带宽限制=链路长度带宽−距离积
带
宽
限
制
=
带
宽
−
距
离
积
链
路
长
度
带宽限制={带宽 - 距离积\over 链路长度}\\
带宽限制=链路长度带宽−距离积 
通
信
容
量
:
带
宽
−
距
离
积
f
3
−
d
B
(
电
)
×
L
=
0.35
Δ
(
τ
/
L
)
=
0.35
D
⋅
Δ
λ
f
3
−
d
B
(
光
)
×
L
=
1
2
Δ
(
τ
/
L
)
=
1
2
D
⋅
Δ
λ
D
光
纤
的
色
散
系
数
,
Δ
λ
光
源
的
线
宽
通信容量: 带宽 - 距离积\\ \\ f_{3-dB}(电) × L = {0.35\over \Delta(\tau/L)} = {0.35\over D·\Delta\lambda}\\ \\ f_{3-dB}(光) × L = {1\over 2\Delta(\tau/L)} = {1\over 2D·\Delta\lambda}\\ \\ D光纤的色散系数,\Delta\lambda光源的线宽
通信容量:带宽−距离积 f3−dB(电)×L = Δ(τ/L)0.35=D⋅Δλ0.35 f3−dB(光)×L = 2Δ(τ/L)1=2D⋅Δλ1 D光纤的色散系数,Δλ光源的线宽
2. 光纤的色散类型
模
式
色
散
:
同
一
波
长
在
不
同
模
式
下
传
输
时
,
各
自
的
群
速
度
不
同
材
料
色
散
:
光
线
材
料
本
身
的
折
射
率
n
和
波
长
λ
呈
非
线
性
关
系
,
使
群
速
度
不
同
波
导
色
散
:
同
一
模
式
在
不
同
的
频
率
下
传
输
时
,
群
速
度
不
同
}
色
度
色
散
模式色散:\\同一波长在不同模式下传输时,各自的群速度不同\\ \left. \begin{matrix} 材料色散:\\光线材料本身的折射率n和波长\lambda呈非线性关系,使群速度不同\\ 波导色散:\\同一模式在不同的频率下传输时,群速度不同 \end{matrix} \right\}色度色散
模式色散:同一波长在不同模式下传输时,各自的群速度不同 材料色散:光线材料本身的折射率n和波长λ呈非线性关系,使群速度不同 波导色散:同一模式在不同的频率下传输时,群速度不同 ⎭⎪⎪⎬⎪⎪⎫色度色散
· 模式色散(Intermodal dispersion)
模式色散是由于在多模光纤中,不同模式的光信号在光纤中传输的群速度不同,引起到达光纤末端的时间延迟不同,经光电探测后,各模式混合,使输出光生电流脉冲相对于输入脉冲展宽

· 材料色散(Material dispersion)
由于光纤材料特性的波长依赖性的结果。
群
速
度
:
V
g
=
c
N
g
,
N
g
=
n
−
λ
d
n
d
λ
群速度:V_g={c\over N_g}, N_g =n-\lambda{dn\over d\lambda}
群速度:Vg=Ngc, Ng=n−λdλdn
· 波导色散(Waveguide dispersion)

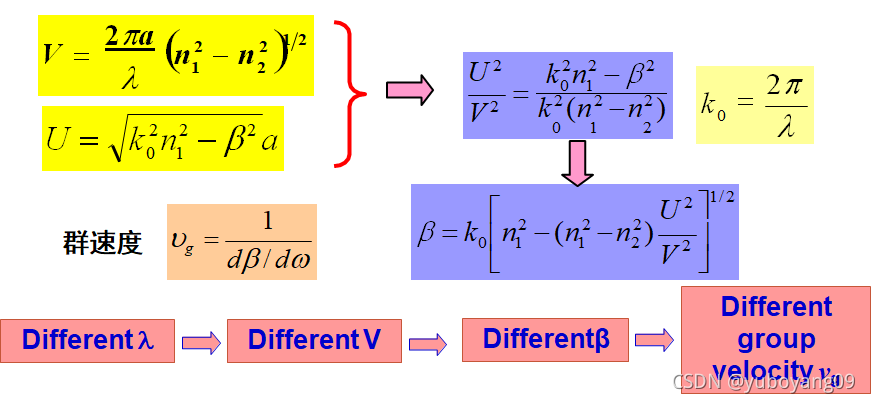
3.单模光纤的色散
标准单模光纤在1550nm(该波长损耗最低)处的色散系数(色散值)约为17ps/nm⋅km
典型代表:G.652光纤
·
大
多
数
已
安
装
的
光
纤
\color{blue}{大多数已安装的光纤}
大多数已安装的光纤
·
色
散
受
限
距
离
短
\color{blue}{色散受限距离短}
色散受限距离短:
2.5
G
b
/
s
\color{red}2.5Gb/s
2.5Gb/s系统色度色散受限距离约为
600
k
m
\color{red}600km
600km
10
G
b
/
s
\color{red}10Gb/s
10Gb/s系统色度色散受限距离约为
40
k
m
\color{red}40km
40km
· 不适用于10Gb/s以上速率传输,但可应用于2.5Gb/s以下速率的DWDM(密集波分复用)
4.色散位移光纤
(DSF,dispersion shifted fiber)


5.非零色散位移光纤

6.色散平坦光纤

7.色散补偿光纤

8.大有效面积光纤

2.5 光线的偏振与保偏光纤
1. 光纤的偏振特性
在单模光纤中,实际上存在两种正交的偏振模式:
L
P
01
x
L
P
01
y
LP^x_{01} LP^y_{01}
LP01x LP01y
在
纤
芯
圆
对
称
\color{blue}纤芯圆对称
纤芯圆对称的光纤中,两种线偏振模式无法区分。
实际单模光纤:
不
完
善
\color{red}不完善
不完善(光纤的弯曲、光纤的椭圆度、内部的残余应力等)
—>
折
射
率
分
布
呈
各
向
异
性
接
\color{red}折射率分布呈各向异性接
折射率分布呈各向异性接(可以简单理解为沿x轴方向和y轴方向的折射率是不一样的);
两
个
偏
振
模
式
的
传
播
速
度
不
同
\color{red} 两个偏振模式的传播速度不同
两个偏振模式的传播速度不同


Δ β = β y − β x , 称 为 双 折 射 参 数 β x = ω n x c , β y = ω n y c Δ τ p = t p y − t p x = ⋅ ⋅ ⋅ ⋅ = Δ β ω Δ τ p 为 两 个 偏 振 模 式 传 输 相 同 距 离 产 生 的 时 延 差 偏 振 模 色 散 与 光 纤 的 双 折 射 参 数 成 正 比 。 \Delta\beta = \beta_y - \beta_x ,称为双折射参数\\\\ \\ \beta_x = {\omega n_x\over c},\beta_y = {\omega n_y\over c}\\ \\ \Delta\tau_p = t_{py} - t_{px}=····={\Delta\beta\over\omega} \\ \\ \\\\\Delta\tau_p为两个偏振模式传输相同距离产生的时延差\\ \\\color{red}偏振模色散与光纤的双折射参数成正比。 Δβ=βy−βx ,称为双折射参数 βx=cωnx,βy=cωny Δτp=tpy−tpx=⋅⋅⋅⋅=ωΔβ Δτp为两个偏振模式传输相同距离产生的时延差 偏振模色散与光纤的双折射参数成正比。
2. 保偏光纤(PMF,Polarization-Maintaining Fiber)
PMF的内应力和非对称性可以有效的将输入光分离为两个独立的偏振模,这种性质叫做双折射
如果输入光是线偏振光并正确对准光纤的偏振方向,则在PMF 中传输的光是单一偏振的,并且保持该偏振方向不变,而且不易受弯曲、微弯、扭转等外界因素的影响。
由光纤中产生双折射的原因可知:由于纤芯的椭圆度或所受应力均可引起光纤中的双折射。
构成高双折射光纤的途径:
(1)增加形状双折射:人为地增加纤芯的椭圆度

(2)增加应力双折射:人为地使光纤包层有非圆对称的应力施加区

集成光电子器件的尾纤通常使用保偏光纤,以保证输入、输出光的偏振态不发生变化。
2.6 光纤的非线性与非线性光纤
1. 光 纤 的 非 线 性 \color{red}1. 光纤的非线性 1.光纤的非线性
在
高
强
度
的
电
磁
场
在\color{blue}高强度的电磁场
在高强度的电磁场
中
,
任
何
电
介
质
对
光
的
响
应
都
会
变
成
非
线
性
。
中,任何电介质对光的响应都会变成非线性。
中,任何电介质对光的响应都会变成非线性。
χ
(
j
)
j
阶
电
极
化
率
,
考
虑
到
光
的
偏
振
效
应
,
χ
(
j
)
为
j
+
1
阶
张
量
线
性
极
化
率
χ
(
1
)
对
P
⃗
的
贡
献
是
主
要
的
χ
(
2
)
对
二
次
谐
波
的
产
生
、
和
频
运
转
等
非
线
性
效
应
;
\chi^{(j)}j阶电极化率,考虑到光的偏振效应,\chi^{(j)}为j+1阶张量\\ 线性极化率\chi^{(1)}对\vec P的贡献是主要的\\\chi^{(2)}对\color{red}{二次谐波的产生、和频运转等非线性效应};
χ(j)j阶电极化率,考虑到光的偏振效应,χ(j)为j+1阶张量线性极化率χ(1)对P的贡献是主要的χ(2)对二次谐波的产生、和频运转等非线性效应;
只
有
在
某
些
分
子
结
构
只有在某些分子结构
只有在某些分子结构
非
反
演
对
称
的
介
质
中
才
不
为
零
\color{red}非反演对称的介质中才不为零
非反演对称的介质中才不为零
S
i
O
2
分
子
是
对
称
的
结
构
,
因
而
对
石
英
玻
璃
χ
(
2
)
等
于
0
;
SiO_2分子是对称的结构,因而对石英玻璃\chi^{(2)}等于0;
SiO2分子是对称的结构,因而对石英玻璃χ(2)等于0;
光
线
通
常
不
显
示
二
阶
非
线
性
效
应
光线通常不显示二阶非线性效应
光线通常不显示二阶非线性效应
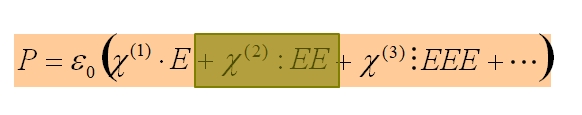
ε
0
真
空
中
的
介
电
常
数
\varepsilon_0真空中的介电常数
ε0真空中的介电常数
所
有
的
非
线
性
效
应
均
与
信
号
光
功
率
的
强
度
所有的非线性效应均与\color{blue}{信号光功率的强度}
所有的非线性效应均与信号光功率的强度
有
关
,
当
输
入
信
号
光
功
率
超
过
一
定
阈
值
时
便
会
引
起
非
线
性
效
应
:
有关,当输入信号光功率超过一定阈值时便会引起非线性效应:
有关,当输入信号光功率超过一定阈值时便会引起非线性效应:
1.
非
线
性
折
射
率
变
化
1.\color{red}非线性折射率变化
1.非线性折射率变化
光
纤
折
射
率
随
光
强
的
变
化
而
变
化
光纤折射率随光强的变化而变化
光纤折射率随光强的变化而变化
自
相
位
调
制
(
S
P
M
,
S
e
l
f
P
h
a
s
e
M
o
d
u
l
a
t
i
o
n
)
自相位调制(SPM,Self Phase Modulation)
自相位调制(SPM,SelfPhaseModulation)
交
叉
相
位
调
制
(
X
P
M
,
C
r
o
s
s
P
h
a
s
e
M
o
d
u
l
a
t
i
o
n
)
交叉相位调制(XPM,Cross Phase Modulation)
交叉相位调制(XPM,CrossPhaseModulation)
四
波
混
频
(
F
W
M
,
F
o
u
r
W
a
v
e
M
i
x
i
n
g
)
四波混频(FWM,Four Wave Mixing)
四波混频(FWM,FourWaveMixing)
2
.
非
线
性
非
弹
性
散
射
2.\color{red}非线性非弹性散射
2.非线性非弹性散射
光
信
号
与
光
纤
中
分
子
的
相
互
作
用
光信号与光纤中分子的相互作用
光信号与光纤中分子的相互作用
受
激
拉
曼
散
射
(
S
R
S
,
S
t
i
m
u
l
a
t
e
d
R
a
m
a
n
S
c
a
t
t
e
r
i
n
g
)
受激拉曼散射(SRS, Stimulated Raman Scattering)
受激拉曼散射(SRS, Stimulated Raman Scattering)
受
激
布
里
渊
散
射
(
S
B
S
,
S
t
i
m
u
l
a
t
e
d
B
r
i
l
l
o
u
i
n
S
c
a
t
t
e
r
i
n
g
)
受激布里渊散射(SBS, Stimulated Brillouin Scattering)
受激布里渊散射(SBS, Stimulated Brillouin Scattering)
\\
基 本 参 量 { 有 效 长 度 有 效 面 积 基本参量 \begin{cases} 有效长度& \text{}\\ 有效面积&\text{} \end{cases} 基本参量 {有效长度有效面积
有 效 长 度 L e f f : 假 设 在 L e f f 内 光 强 不 变 。 有效长度L_{eff}:假设在L_{eff}内光强不变。 有效长度Leff:假设在Leff内光强不变。
L
e
f
f
=
⋅
⋅
⋅
=
1
−
e
−
α
L
α
L_{eff} =···={1-e^{-\alpha L}\over\alpha}
Leff=⋅⋅⋅=α1−e−αL
α
=
d
P
d
z
表
示
传
输
单
位
距
离
后
功
率
的
改
变
量
\alpha ={dP\over dz}表示传输单位距离后功率的改变量
α=dzdP表示传输单位距离后功率的改变量
光
强
反
比
于
距
光
纤
轴
心
的
距
离
。
为
了
分
析
方
便
。
截
面
采
用
有
效
面
积
A
e
f
f
表
示
,
假
设
A
e
f
f
内
光
强
分
布
均
匀
光强反比于距光纤轴心的距离。为了分析方便。截面采用有效面积A_{eff}表示,假设A_{eff}内光强分布均匀
光强反比于距光纤轴心的距离。为了分析方便。截面采用有效面积Aeff表示,假设Aeff内光强分布均匀
普
通
单
模
光
纤
的
A
e
f
f
≈
80
μ
m
2
普通单模光纤的A_{eff} ≈ 80\mu m^2
普通单模光纤的Aeff≈80μm2
色
散
位
移
光
纤
的
A
e
f
f
≈
55
μ
m
2
色散位移光纤的A_{eff} ≈ 55\mu m^2
色散位移光纤的Aeff≈55μm2
色
散
补
偿
光
纤
的
A
e
f
f
≈
20
μ
m
2
色散补偿光纤的A_{eff} ≈ 20\mu m^2
色散补偿光纤的Aeff≈20μm2
克 尔 效 应 \color{blue}克尔效应 克尔效应
光
纤
的
折
射
率
可
表
示
为
:
光纤的折射率可表示为:
光纤的折射率可表示为: 
自
相
位
调
制
(
S
P
M
,
S
e
l
f
P
h
a
s
e
M
o
d
u
l
a
t
i
o
n
)
自相位调制(SPM,Self Phase Modulation)
自相位调制(SPM,SelfPhaseModulation)
交
叉
相
位
调
制
(
X
P
M
,
C
r
o
s
s
P
h
a
s
e
M
o
d
u
l
a
t
i
o
n
)
交叉相位调制(XPM,Cross Phase Modulation)
交叉相位调制(XPM,CrossPhaseModulation)
:
都
是
由
折
射
率
的
变
化
引
起
的
光
脉
冲
的
相
位
调
制
:\color{red}都是由折射率的变化引起的光脉冲的相位调制
:都是由折射率的变化引起的光脉冲的相位调制
S
P
M
\color{blue}SPM
SPM
是
指
光
场
在
光
纤
内
传
播
时
,
光
场
本
身
引
起
的
相
移
是指光场在光纤内传播时,\color{blue}光场本身引起的相移
是指光场在光纤内传播时,光场本身引起的相移
在
其
他
方
面
,
S
P
M
与
超
短
脉
冲
的
频
谱
展
宽
在其他方面,SPM与超短脉冲的\color{green}频谱展宽
在其他方面,SPM与超短脉冲的频谱展宽
有
关
;
有关;
有关;
在
光
纤
的
反
常
色
散
区
与
光
孤
子
的
存
在
在光纤的反常色散区与\color{green}光孤子的存在
在光纤的反常色散区与光孤子的存在
有
关
。
有关。
有关。
X
P
M
\color{blue}XPM
XPM
是
由
不
同
波
长
、
传
输
方
向
或
偏
振
态
的
脉
冲
共
同
传
输
时
,
是由不同波长、传输方向或偏振态的脉冲共同传输时,
是由不同波长、传输方向或偏振态的脉冲共同传输时,
一
种
光
场
引
起
另
一
种
光
场
的
非
线
性
相
移
。
\color{blue}一种光场引起另一种光场的非线性相移。
一种光场引起另一种光场的非线性相移。
在
其
他
方
面
,
X
P
M
与
共
同
传
输
光
脉
冲
的
不
对
称
频
谱
展
宽
在其他方面,XPM与共同传输光脉冲的\color{green}不对称频谱展宽
在其他方面,XPM与共同传输光脉冲的不对称频谱展宽
有
关
;
有关;
有关;
自
相
位
调
制
S
P
M
\color{blue}自相位调制SPM
自相位调制SPM
:
将
引
起
光
纤
中
传
输
脉
冲
的
频
谱
展
宽
:将引起\color{red}光纤中传输脉冲的频谱展宽
:将引起光纤中传输脉冲的频谱展宽
脉
冲
频
率
展
宽
的
程
度
与
脉冲频率展宽的程度与
脉冲频率展宽的程度与
脉
冲
的
形
状
\color{red}脉冲的形状
脉冲的形状
有
关
。
有关。
有关。
将
引
起
连
续
波
频
谱
的
展
宽
将引起\color{red}连续波频谱的展宽
将引起连续波频谱的展宽
连
续
光
在
光
纤
中
传
播
时
,
S
P
M
也
能
导
致
频
谱
的
展
宽
。
连续光在光纤中传播时,SPM也能导致频谱的展宽。
连续光在光纤中传播时,SPM也能导致频谱的展宽。
物
理
机
制
:
部
分
相
干
光
的
强
度
和
相
位
都
在
起
伏
,
S
P
M
将
前
强
度
的
起
伏
转
变
成
附
加
相
位
的
起
伏
,
并
使
频
谱
展
宽
物理机制:部分相干光的强度和相位都在起伏,SPM将前强度的起伏转变成附加相位的起伏,并使频谱展宽
物理机制:部分相干光的强度和相位都在起伏,SPM将前强度的起伏转变成附加相位的起伏,并使频谱展宽
交
叉
相
位
调
制
X
P
M
\color{blue}交叉相位调制XPM
交叉相位调制XPM
:
将
引
起
调
制
的
不
稳
定
性
:将引起\color{red}调制的不稳定性
:将引起调制的不稳定性
许
多
非
线
性
系
统
都
表
现
出
一
种
不
稳
定
性
许多非线性系统都表现出一种\color{red}不稳定性
许多非线性系统都表现出一种不稳定性
—
—
由
于
非
线
性
和
色
散
效
应
之
间
的
互
作
用
导
致
的
对
稳
态
的
调
制
。
——由于非线性和色散效应之间的互作用导致的对稳态的调制。
——由于非线性和色散效应之间的互作用导致的对稳态的调制。
光
纤
中
的
调
制
不
稳
定
性
在
频
域
上
光纤中的调制不稳定性在\color{blue}频域上
光纤中的调制不稳定性在频域上
表
现
为
谱
线
旁
瓣
的
产
生
,
在
表现为谱线旁瓣的产生,在
表现为谱线旁瓣的产生,在
时
域
上
\color{blue}时域上
时域上
使
连
续
或
准
连
续
光
分
裂
成
一
系
列
短
脉
冲
串
。
使连续或准连续光分裂成一系列短脉冲串。
使连续或准连续光分裂成一系列短脉冲串。
四
波
混
频
(
F
W
M
,
F
o
u
r
W
a
v
e
M
i
x
i
n
g
)
四波混频(FWM,Four Wave Mixing)
四波混频(FWM,FourWaveMixing)
在
量
子
力
学
术
语
中
,
一
个
或
几
个
光
波
的
光
子
被
湮
灭
,
同
时
产
生
了
几
个
不
同
频
率
的
新
光
子
且
在
此
参
量
作
用
过
程
中
,
在量子力学术语中,一个或几个光波的光子被湮灭,同时产生了几个不同 频率的新光子且在此参量作用过程中,
在量子力学术语中,一个或几个光波的光子被湮灭,同时产生了几个不同频率的新光子且在此参量作用过程中,
净
能
量
和
动
量
是
守
恒
的
,
这
个
过
程
称
作
四
波
混
频
。
净能量和动量是守恒的,这个过程称作\color{blue}四波混频。
净能量和动量是守恒的,这个过程称作四波混频。
只
有
当
相
位
失
配
几
乎
为
零
时
只有当\color{red}相位失配几乎为零时
只有当相位失配几乎为零时
,
才
会
发
生
显
著
的
四
波
混
频
过
程
。
,才会发生显著的四波混频过程。
,才会发生显著的四波混频过程。
当
3
个
波
长
的
F
W
M
时
,
频
率
产
生
的
规
则
如
下
:
当3个波长的FWM时,频率产生的规则如下:
当3个波长的FWM时,频率产生的规则如下:
V
i
j
k
=
V
i
+
V
j
−
V
k
i
,
j
≠
k
V_{ijk}=V_i+V_j-V_k i,j≠k
Vijk=Vi+Vj−Vk i,j=k
产
物
个
数
:
产物个数:
产物个数:
M
=
N
2
(
N
−
1
)
2
,
N
为
参
与
F
W
M
的
波
长
数
。
M={N^2(N-1)\over2},N为参与FWM的波长数。
M=2N2(N−1),N为参与FWM的波长数。
F
W
M
的
特
点
:
\color{red}FWM的特点:
FWM的特点:
其
影
响
有
赖
于
相
互
作
用
信
号
之
间
的
相
位
关
系
。
其影响有赖于\color{red}相互作用信号之间的相位关系。
其影响有赖于相互作用信号之间的相位关系。
色
散
位
移
光
纤
\color{red}色散位移光纤
色散位移光纤
中
的
色
散
值
很
低
,
F
W
M
效
率
要
高
得
多
。
中的色散值很低,FWM效率要高得多。
中的色散值很低,FWM效率要高得多。
在
色
散
位
移
光
纤
中
,
信
道
数
增
加
时
,
会
产
生
更
多
的
F
W
M
项
。
在色散位移光纤中,信道数增加时,会产生更多的FWM项。
在色散位移光纤中,信道数增加时,会产生更多的FWM项。
信
道
间
隔
减
小
\color{red}信道间隔减小
信道间隔减小
时
,
相
位
失
配
减
小
,
F
W
M
效
率
增
加
。
时,相位失配减小,FWM效率增加。
时,相位失配减小,FWM效率增加。
信
号
功
率
增
加
\color{red}信号功率增加
信号功率增加
,
F
W
M
呈
指
数
增
加
,FWM呈指数增加
,FWM呈指数增加
降
低
F
W
M
的
措
施
:
\color{red}降低FWM的措施:
降低FWM的措施:
1.
仔
细
选
择
各
信
道
的
位
置
1.\color{red}仔细选择各信道的位置
1.仔细选择各信道的位置
,
使
得
那
些
拍
频
项
不
与
信
道
带
宽
范
围
重
叠
,使得那些拍频项不与信道带宽范围重叠
,使得那些拍频项不与信道带宽范围重叠
2.
增
加
信
道
间
隔
2.\color{blue}增加信道间隔
2.增加信道间隔
,
增
加
信
道
之
间
的
群
速
度
不
匹
配
,增加信道之间的群速度不匹配
,增加信道之间的群速度不匹配
3.
增
加
光
纤
的
有
效
截
面
A
e
f
f
3.\color{red}增加光纤的有效截面A_{eff}
3.增加光纤的有效截面Aeff
,
降
低
光
纤
中
光
功
率
密
度
,降低光纤中光功率密度
,降低光纤中光功率密度
4.
针
对
不
同
波
长
信
道
引
入
延
时
4.针对不同波长信道\color{green}引入延时
4.针对不同波长信道引入延时
,
从
而
扰
乱
不
同
波
长
信
道
的
相
位
关
系
,从而扰乱不同波长信道的相位关系
,从而扰乱不同波长信道的相位关系
\\
受
激
拉
曼
散
射
(
S
R
S
,
S
t
i
m
u
l
a
t
e
d
R
a
m
a
n
S
c
a
t
t
e
r
i
n
g
)
\color{blue} 受激拉曼散射(SRS, Stimulated Raman Scattering)
受激拉曼散射(SRS, Stimulated Raman Scattering)
受
激
布
里
渊
散
射
(
S
B
S
,
S
t
i
m
u
l
a
t
e
d
B
r
i
l
l
o
u
i
n
S
c
a
t
t
e
r
i
n
g
)
\color{blue}受激布里渊散射(SBS, Stimulated Brillouin Scattering)
受激布里渊散射(SBS, Stimulated Brillouin Scattering)
\\
受
激
拉
曼
散
射
(
S
R
S
,
S
t
i
m
u
l
a
t
e
d
R
a
m
a
n
S
c
a
t
t
e
r
i
n
g
)
\color{blue} 受激拉曼散射(SRS, Stimulated Raman Scattering)
受激拉曼散射(SRS, Stimulated Raman Scattering)
一
个
能
量
较
高
(
较
短
波
长
)
的
入
射
泵
浦
光
子
产
生
一
个
较
低
能
量
(
波
长
较
长
)
的
光
子
(
斯
托
克
斯
波
)
,
剩
余
的
能
量
一个能量较高(较短波长)的入射泵浦光子产生一个较低能量(波长较长)的光子(斯托克斯波),剩余的能量
一个能量较高(较短波长)的入射泵浦光子产生一个较低能量(波长较长)的光子(斯托克斯波),剩余的能量
以
分
子
振
荡
的
形
式
(
光
声
子
)
以分子振荡的形式(\color{red}光声子)
以分子振荡的形式(光声子)
被
介
质
吸
收
,
这
种
现
象
称
为
受
激
拉
曼
散
射
(
S
R
S
)
被介质吸收,这种现象称为受激拉曼散射(SRS)
被介质吸收,这种现象称为受激拉曼散射(SRS)
基
本
特
点
:
\color{red}基本特点:
基本特点:
1.
S
R
S
是
光
子
受
到
振
动
分
子
散
射
所
产
生
的
;
1. SRS是光子受到振动分子散射所产生的;
1. SRS是光子受到振动分子散射所产生的;
S
R
S
同
时
存
在
于
光
传
输
方
向
或
者
与
之
相
反
的
方
向
SRS同时存在于光传输方向或者与之相反的方向
SRS同时存在于光传输方向或者与之相反的方向
2.
光
纤
中
的
斯
托
克
斯
波
迅
速
增
长
,
以
致
大
部
分
泵
浦
光
能
量
转
移
到
斯
托
克
斯
波
上
,
实
现
对
斯
托
克
斯
波
的
增
益
。
2. 光纤中的斯托克斯波迅速增长,以致大部分泵浦光能量转移到斯托克斯波上,实现对斯托克斯波的增益。
2. 光纤中的斯托克斯波迅速增长,以致大部分泵浦光能量转移到斯托克斯波上,实现对斯托克斯波的增益。

S
R
S
使
W
D
M
信
道
中
短
波
长
能
量
向
长
波
长
转
移
,
导
致
:
SRS使WDM信道中短波长能量向长波长转移,导致:
SRS使WDM信道中短波长能量向长波长转移,导致:
1.
短
波
长
能
量
损
耗
1.短波长能量损耗
1.短波长能量损耗
2.
长
波
长
信
号
被
串
扰
2.长波长信号被串扰
2.长波长信号被串扰
S
R
S
引
起
D
W
D
M
不
同
信
道
之
间
发
生
耦
合
,
导
致
串
扰
SRS引起DWDM不同信道之间发生耦合,\color{red}导致串扰
SRS引起DWDM不同信道之间发生耦合,导致串扰
长
波
长
信
号
被
短
波
长
信
号
放
大
,
引
起
信
道
功
率
不
平
衡
。
仅
当
两
个
波
长
信
号
均
处
于
高
电
平
状
态
长波长信号被短波长信号放大,引起信道功率不平衡。仅当两个波长信号均处于\color{red}高电平状态
长波长信号被短波长信号放大,引起信道功率不平衡。仅当两个波长信号均处于高电平状态
才
会
发
生
S
R
S
。
才会发生SRS。
才会发生SRS。
拉
曼
增
益
的
物
理
效
应
:
\color{blue}拉曼增益的物理效应:
拉曼增益的物理效应:
当
频
率
为
ω
p
的
连
续
光
泵
入
光
纤
中
进
行
传
播
时
,
如
有
一
个
频
率
为
ω
s
的
探
测
光
与
泵
浦
光
同
时
进
入
光
纤
,
只
要
其
频
率
差
ω
p
当频率为\omega_p的连续光泵入光纤中进行传播时,如有一个频率为\omega_s的探测光与泵浦光同时进入光纤,只要其频率差\omega_p
当频率为ωp的连续光泵入光纤中进行传播时,如有一个频率为ωs的探测光与泵浦光同时进入光纤,只要其频率差ωp
−
ω
s
在
光
纤
的
拉
曼
增
益
的
带
宽
范
围
之
内
,
探
测
波
就
会
因
拉
曼
增
益
而
获
得
放
大
。
-\omega_s在光纤的拉曼增益的带宽范围之内,探测波就会因拉曼增益而获得放大。
−ωs在光纤的拉曼增益的带宽范围之内,探测波就会因拉曼增益而获得放大。
注
:
ω
p
−
ω
s
<
16
T
H
z
时
,
拉
曼
增
益
g
R
随
ω
p
−
ω
s
的
增
加
而
线
性
增
加
注:\omega_p - \omega_s<16THz时,拉曼增益g_R随\omega_p - \omega_s的增加而线性增加
注:ωp−ωs<16THz时,拉曼增益gR随ωp−ωs的增加而线性增加
阈
值
功
率
:
\color{pink}阈值功率:
阈值功率:
输
入
光
有
一
半
功
率
转
化
到
斯
托
克
斯
光
时
的
输
入
功
率
。
P
t
h
≈
16
A
e
f
f
(
g
R
,
p
e
a
k
L
e
f
f
)
,
理
论
计
算
阈
值
P
t
h
≈
1.067
W
输入光有一半功率转化到斯托克斯光时的输入功率。P_{th}≈{16A_{eff}\over (g_{R,peak L_{eff}})},理论计算阈值P_{th}≈1.067W
输入光有一半功率转化到斯托克斯光时的输入功率。Pth≈(gR,peakLeff)16Aeff,理论计算阈值Pth≈1.067W
应
用
:
拉
曼
激
光
器
和
光
放
大
器
应用:\color{blue}拉曼激光器和光放大器
应用:拉曼激光器和光放大器
受
激
布
里
渊
散
射
(
S
B
S
,
S
t
i
m
u
l
a
t
e
d
B
r
i
l
l
o
u
i
n
S
c
a
t
t
e
r
i
n
g
)
\color{blue}受激布里渊散射(SBS, Stimulated Brillouin Scattering)
受激布里渊散射(SBS, Stimulated Brillouin Scattering)
泵
浦
波
、
斯
托
克
斯
波
通
过
声
波
进
行
的
非
线
性
互
作
用
,
泵
浦
波
通
过
电
致
伸
缩
产
生
声
波
,
然
后
引
起
介
质
折
射
率
的
周
期
性
泵浦波、斯 托克斯波通过声波进行的非线性互作用,泵浦波通过电致伸缩产生声波,然后引起介质折射率的周期性
泵浦波、斯托克斯波通过声波进行的非线性互作用,泵浦波通过电致伸缩产生声波,然后引起介质折射率的周期性
调
制
调制
调制
,
在
这
个
过
程
中
,
泵
浦
波
的
能
量
转
移
给
斯
托
克
斯
波
。
,在这个过程中,泵 浦波的能量转移给斯托克斯波。
,在这个过程中,泵浦波的能量转移给斯托克斯波。
满
足
能
量
和
动
量
守
恒
:
Ω
B
=
ω
p
−
ω
s
,
k
A
=
k
p
−
k
s
满足能量和动量守恒:Ω_B = \omega_p - \omega_s, k_A =k_p -k_s
满足能量和动量守恒:ΩB=ωp−ωs, kA=kp−ks
当
入
纤
功
率
高
于
一
个
阈
值
的
时
候
发
生
S
B
S
现
象
,
入
射
光
的
一
部
分
能
量
转
化
为
反
向
传
播
的
斯
托
克
斯
光
,
造
成
正
向
传
播
当入纤功率高于一个阈值的时候发生SBS现象,入射光的一部分 能量转化为反向传播的斯托克斯光,造成\color{red}正向传播
当入纤功率高于一个阈值的时候发生SBS现象,入射光的一部分能量转化为反向传播的斯托克斯光,造成正向传播
的
光
信
号
的
衰
减
\color{red}的光信号的衰减
的光信号的衰减
。
另
外
,
反
向
光
入
射
到
光
源
会
造
成
光
源
工
作
不
稳
定
。
。另外,反向光入射到光源会造成光源工作不稳定。
。另外,反向光入射到光源会造成光源工作不稳定。
布
里
渊
频
移
\color{pink}布里渊频移
布里渊频移
:
斯
托
克
斯
光
相
对
于
入
射
光
的
频
率
差
称
为
布
里
渊
频
移
:
:斯托克斯光相对于入射光的频率差称为布里渊频移:
:斯托克斯光相对于入射光的频率差称为布里渊频移:
V
B
=
2
n
V
s
λ
V_B = {2nV_s\over \lambda}
VB=λ2nVs
其
中
,
n
是
介
质
折
射
率
,
V
s
是
介
质
中
声
波
传
播
速
率
其中,n是介质折射率,V_s是介质中\color{red}声波传播速率
其中,n是介质折射率,Vs是介质中声波传播速率
阈
值
功
率
:
阈值功率:
阈值功率:

减
小
S
B
S
损
伤
的
办
法
\color{red}减小SBS损伤的办法
减小SBS损伤的办法
1.
保
持
每
个
W
D
M
信
道
光
功
率
比
较
小
,
减
小
E
D
F
A
间
的
跨
度
1.保持每个WDM信道光功率比较小,减小EDFA间的跨度
1.保持每个WDM信道光功率比较小,减小EDFA间的跨度
⋅
减
少
E
D
F
A
的
输
出
功
率
·\color{blue}减少EDFA的输出功率
⋅减少EDFA的输出功率
⋅
减
小
E
D
F
A
之
间
的
跨
度
·\color{blue}减小EDFA之间的跨度
⋅减小EDFA之间的跨度
2.
增
加
光
源
线
宽
,
光
源
线
宽
越
宽
,
S
B
S
功
率
阈
值
越
高
,
但
是
会
付
出
色
散
的
代
价
2.增加光源线宽,光源线宽越宽,SBS功率阈值越高,但是会付出色散的代价
2.增加光源线宽,光源线宽越宽,SBS功率阈值越高,但是会付出色散的代价
光 纤 的 非 线 性 效 应 \color{red} 光纤的非线性效应 光纤的非线性效应
| 效应 | 单信道 | 多信道 |
|---|---|---|
| 折射率效应(光强度波动引起的折射率的调制) | 自相位调制(SPM) | 交叉相位调制(XPM)、四波混频)(FWM) |
| 散射效应 | 受激布里渊散射(SBS) | 受激拉曼散射(SRS) |
光 纤 的 非 线 性 阈 值 功 率 \color{red} 光纤的非线性阈值功率 光纤的非线性阈值功率
| 10 μ m \mu m μm单模 | 50 μ m \mu m μm多模 | |
|---|---|---|
| 受激拉曼散射(SRS) | 3.3W | 150W |
| 受激布里渊散射(SBS) | 9.8mW | 440mW |
| 自相位调制(SPM) | 185mW | 5W |
2. 非 线 性 光 纤 \color{red}2.非线性光纤 2.非线性光纤
掺
杂
光
纤
掺杂光纤
掺杂光纤
掺
杂
光
纤
{
掺
铒
光
纤
C、L波段光纤放大器,光纤激光器
掺
镨
光
纤
掺镨光纤放大器(PDFA)
掺
铥
光
纤
掺铥光纤放大器(TDFA)
掺
锗
光
纤
光纤光栅
掺杂光纤 \begin{cases} 掺铒光纤& \text{C、L波段光纤放大器,光纤激光器}\\ 掺镨光纤&\text{掺镨光纤放大器(PDFA)} \\ 掺铥光纤& \text{掺铥光纤放大器(TDFA)}\\ 掺锗光纤& \text{光纤光栅}\\\end{cases}
掺杂光纤⎩⎪⎪⎪⎨⎪⎪⎪⎧掺铒光纤掺镨光纤掺铥光纤掺锗光纤C、L波段光纤放大器,光纤激光器掺镨光纤放大器(PDFA)掺铥光纤放大器(TDFA)光纤光栅
光
子
晶
体
光
纤
(
P
C
F
,
p
h
o
t
o
n
i
c
c
r
y
s
t
a
l
f
i
b
e
r
)
光子晶体光纤(PCF,photonic crystal fiber)
光子晶体光纤(PCF,photoniccrystalfiber)
折
射
率
导
光
机
理
\color{blue}折射率导光机理
折射率导光机理
光
子
能
隙
导
光
机
理
\color{blue}光子能隙导光机理
光子能隙导光机理
降
低
非
线
性
\color{green}降低非线性
降低非线性
方
法
:
通
过
增
加
P
C
F
纤
芯
空
气
孔
直
径
,
即
P
C
F
的
有
效
面
积
来
降
低
单
位
有
效
面
积
上
的
光
强
方法:通过增加PCF纤芯空气孔直径,即PCF的有效面积来降低单位有效面积上的光强
方法:通过增加PCF纤芯空气孔直径,即PCF的有效面积来降低单位有效面积上的光强
应
用
:
在
大
功
率
激
光
传
输
应用:在\color{red}大功率激光传输
应用:在大功率激光传输
应
用
方
面
有
重
要
意
义
应用方面有重要意义
应用方面有重要意义
提
高
非
线
性
\color{green}提高非线性
提高非线性
方
法
:
通
过
合
理
设
计
P
C
F
的
纤
芯
结
构
,
使
其
纤
芯
直
径
减
小
方法:通过合理设计PCF的纤芯结构,使其\color{blue}{纤芯直径减小}
方法:通过合理设计PCF的纤芯结构,使其纤芯直径减小
(
1
μ
m
)
,
同
时
具
有
大
的
折
射
率
差
(~1\mu m),同时具有\color{blue}大的折射率差
( 1μm),同时具有大的折射率差
从
而
使
得
光
纤
具
有
非
常
小
的
有
效
面
积
从而使得光纤具有\color{red}非常小的有效面积
从而使得光纤具有非常小的有效面积
应
用
:
在
非
线
性
频
率
变
换
、
超
连
续
谱
产
生
、
光
开
关
应用:在\color{red}非线性频率变换、超连续谱产生、光开关
应用:在非线性频率变换、超连续谱产生、光开关
等
领
域
有
重
要
的
应
用
前
景
等领域有重要的应用前景
等领域有重要的应用前景
2.7 光纤的最新发展
光子晶体光纤(PCF,photonic crystal fibers)
特点及应用:
(1) 大数值孔径:即使入射角很大,也可容易将光耦合进入光纤.
(2) 无截止单模特性:在很宽的波长范围内(458~1550nm)仍可维持单模行为.
(3) 非线性特性:
·极高:通过改变空气孔间距可以调节有效模场面积 一> 有利于飞秒脉冲激光的产生
·极低:空气芯光子晶体光纤可以避免传统光纤纤芯的吸收或非线性效应 一> 高功率光纤激光器或放大器
(4) 良好的色散特性
(5) 良好的保偏特性:即使受到弯曲或扭曲仍可保持其相位及原始的偏振特性
塑料光纤(POF,polymer optical fibers)
POF的数值孔径NA=0.3~0.5, 芯径=0.5~1mm,连接时不必苛求精确对准.
POF还具有抗弯曲,抗震动,施工方便,重量轻,节约金属资源等资源
POF适用于高速短距离通信,尤其是连接点较多的局域网和接入网




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








