红尾鹰优化算法(Red-tailed hawk algorithm,RTH)是期刊“Scientific Reports”的智能优化算法
01.引言
这项研究提出了一种新的受自然启发的元启发式优化算法,称为红尾鹰算法(RTH)。作为捕食者,红尾鹰有从发现猎物到猛扑阶段的狩猎策略。狩猎过程分为三个阶段。在高空翱翔阶段,红尾鹰探索搜索空间,确定猎物所在的区域。在低空翱翔阶段,红尾在猎物周围选定的区域内移动,选择最佳位置进行捕猎。然后,红尾在弯腰和俯冲阶段摆动并击中目标。该算法模仿红尾鹰的猎物狩猎方法来解决现实世界的优化问题。所提出的 RTH 算法的性能已针对三类问题进行了评估。第一类包括三种特定类型的优化问题:22 个标准基准函数,包括单峰、多峰和固定维多峰函数、IEEE 进化计算大会 2020 (CEC2020) 和 IEEE CEC2022。将所提出的算法与八种最新算法进行比较,以确认其对解决这些问题的贡献。考虑的算法有农田肥力优化算法 (FO)、非洲秃鹫优化算法 (AVOA)、山羚优化算法 (MGO)、大猩猩部队优化算法 (GTO)、COOT 算法、饥饿游戏搜索 (HGS)、天鹰优化算法 (AO) 和哈里斯老鹰优化(HHO)。比较结果的准确性、鲁棒性和收敛速度。第二类包括七个现实世界的工程问题,将考虑对 RTH 性能与其他已发表的结果进行深入比较。最后,将执行质子交换膜燃料电池 (PEMFC) 提取参数,以评估具有复杂问题的算法。所提出的算法将与几篇已发表的论文进行比较,以验证其性能。每个类别的最终结果证实了所提出的 RTH 算法在大多数情况下提供更高性能的能力。对于第一类,RTH大多以更快的收敛速度获得了大多数函数的最优解。在解决实际工程问题或提取 PEMFC 参数时,RTH 为第二类和第三类提供了更好的性能。
02.优化算法的流程
红尾鹰优化算法(Red-tailed hawk algorithm,RTH)模仿红尾鹰的狩猎行为。在每个狩猎阶段采取的行动都会被呈现和建模。该算法包括高翱翔、低翱翔、弯腰俯冲三个阶段。

03.部分代码
function [Cost, Pos, Convergence_curve]=RTH(N,Tmax,low,high,dim,fobj)
Xbestcost = inf; Xbestpos = rand(N,dim);
for i=1:N
Xpos(i,:) = low+(high-low).*rand(1,dim);
Xcost(i)=fobj(Xpos(i,:));
if Xcost(i) < Xbestcost
Xbestpos = Xpos(i,:);
Xbestcost = Xcost(i);
end
end
A=15;
R0=0.5;
r = 1.5;
for t=1:Tmax
%% 1- High Soaring
Xmean=mean(Xpos);
TF = 1+sin(2.5-t/Tmax); % TF
for i=1:N
Xnewpos=Xbestpos+(Xmean-Xpos(i,:)).*Levy(dim)*TF;
Xnewpos = max(Xnewpos, low);
Xnewpos = min(Xnewpos, high);
Xnewcost=fobj(Xnewpos);
if Xnewcost<Xcost(i)
Xpos(i,:) = Xnewpos;
Xcost(i)= Xnewcost;
if Xcost(i) < Xbestcost
Xbestpos= Xpos(i,:);
Xbestcost=Xcost(i);
end
end
end
%% 2- Low Soaring
Xmean=mean(Xpos);
for i=1:N-1
aa=randperm(N);
Xpos=Xpos(aa,:);
Xcost=Xcost(aa);
[x y]=polr(A,R0,N,t,Tmax,r);
StepSize=Xpos(i,:)-Xmean;
Xnewpos = Xbestpos +(y(i)+x(i))*StepSize;
Xnewpos = max(Xnewpos, low);
Xnewpos = min(Xnewpos, high);
Xnewcost=fobj(Xnewpos);
if Xnewcost<Xcost(i)
Xpos(i,:) = Xnewpos;
Xcost(i)= Xnewcost;
if Xcost(i) < Xbestcost
Xbestpos= Xpos(i,:);
Xbestcost=Xcost(i);
end
end
end
%% 3- Stopping & Swooping
Xmean=mean(Xpos);
TF = 1+0.5*sin(2.5-t/Tmax);
for i=1:N
b=randperm(N);
Xpos=Xpos(b,:);
Xcost=Xcost(b);
[x y]=polr(A,R0,N,t,Tmax,r);
alpha=(sin(2.5-t/Tmax).^2);
G=2*(1-(t/Tmax));
StepSize1 = 1.*Xpos(i,:) - TF*Xmean;
StepSize2= G.*Xpos(i,:)-TF*Xbestpos;
Xnewpos = alpha*Xbestpos+x(i)*StepSize1+y(i)*StepSize2;
Xnewpos = max(Xnewpos, low);
Xnewpos = min(Xnewpos, high);
Xnewcost=fobj(Xnewpos);
if Xnewcost<Xcost(i)
Xpos(i,:) = Xnewpos;
Xcost(i)= Xnewcost;
if Xcost(i) < Xbestcost
Xbestpos= Xpos(i,:);
Xbestcost=Xcost(i);
end
end
end
Convergence_curve(t)=Xbestcost;
Cost = Xbestcost;
Pos = Xbestpos;
end
function [xR yR]=polr(A,R0,N,t,MaxIt,r)
%// Set parameters
th = (1+t/MaxIt)*A*pi*rand(N,1);
R =(r-t/MaxIt)*R0*rand(N,1);
xR = R.*sin(th);
yR = R.*cos(th);
xR=xR/max(abs(xR));
yR=yR/max(abs(yR));
function o=Levy(d)
beta=1.5;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;v=randn(1,d);step=u./abs(v).^(1/beta);
o=step;04.代码效果图
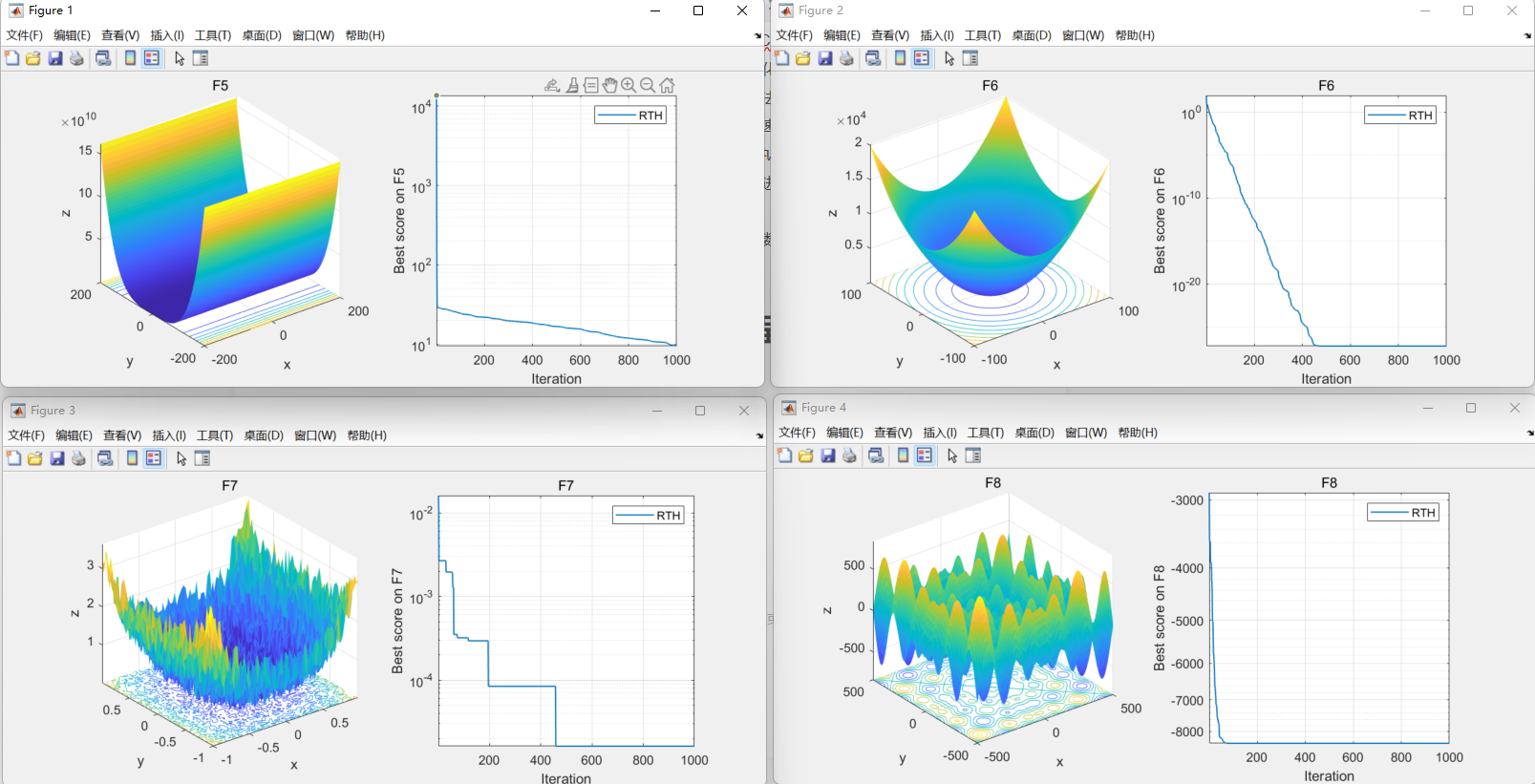
获取代码请关注MATLAB科研小白的个人公众号(即文章下方二维码),并回复智能优化算法本公众号致力于解决找代码难,写代码怵。各位有什么急需的代码,欢迎后台留言~不定时更新科研技巧类推文,可以一起探讨科研,写作,文献,代码等诸多学术问题,我们一起进步。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










