【智能优化算法】瞪羚优化算法(Gazelle optimization algorithm，MGO）-CSDN博客

本文链接：https://blog.csdn.net/yuchunyu12/article/details/138307148

瞪羚优化算法(Gazelle optimization algorithm，MGO）是期刊“Neural Computing and Applications”（IF 5.6）的2023年智能优化算法

01.引言

瞪羚优化算法(Gazelle optimization algorithm，MGO）的灵感来自瞪羚在捕食者主导的环境中的生存能力。每一天，瞪羚都知道，如果它不能跑得比它的捕食者更快，它就会成为当天的肉，为了生存，瞪羚必须不断地逃离它们的捕食者。这些信息对于提出一种新的元启发式算法至关重要，该算法利用瞪羚的生存能力来解决现实世界的优化问题。算法的开发阶段模拟瞪羚在没有捕食者或捕食者跟踪它的情况下平静地吃草。一旦发现捕食者，GOA就进入探索阶段。在探索阶段，瞪羚要跑得比捕食者更快，找到一个安全的避难所。

02.优化算法的流程

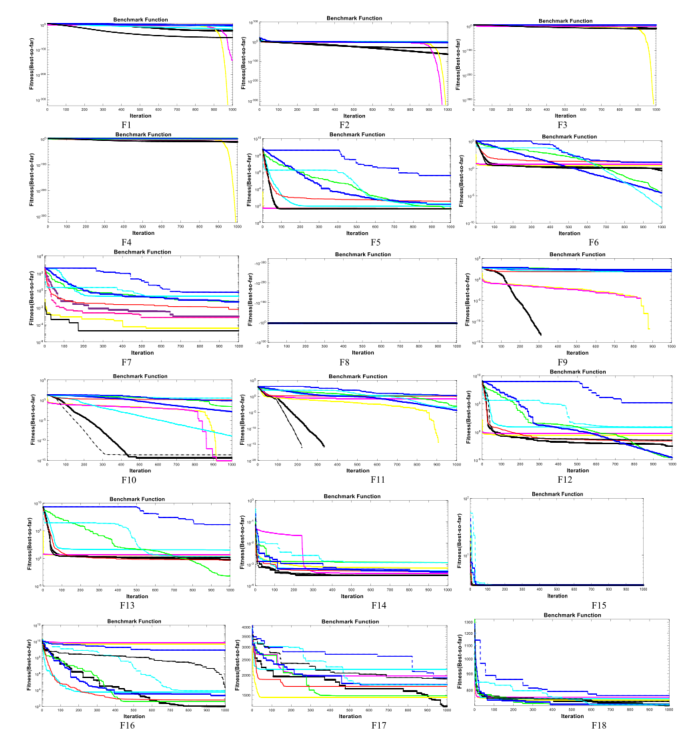
03.论文中算法对比图

04.部分代码

function [BestF,BestX,cnvg]=MGO(N,MaxIter,LB,UB,dim,fobj)
lb=ones(1,dim).*LB;  
ub=ones(1,dim).*UB;
%Initialize the first random population of Gazelles 
X=initialization(N,dim,UB,LB);
% initialize Best Gazelle
BestX=[];
BestFitness=inf;
for i=1:N   
    
    % Calculate the fitness of the population
    Sol_Cost(i,:)=fobj(X(i,:));%#ok
    
    % Update the Best Gazelle if needed
    if Sol_Cost(i,:)<=BestFitness 
        BestFitness=Sol_Cost(i,:); 
        BestX=X(i,:);
    end
end
%mainloop
    for Iter=1:MaxIter
        for i=1:N
            
            RandomSolution=randperm(N,ceil(N/3));
            M=X(randi([(ceil(N/3)),N]),:)*floor(rand)+mean(X(RandomSolution,:)).*ceil(rand);     
            
            % Calculate the vector of coefficients
            cofi = Coefficient_Vector(dim,Iter,MaxIter);
            
            A=randn(1,dim).*exp(2-Iter*(2/MaxIter));
            D=(abs(X(i,:)) + abs(BestX))*(2*rand-1);
                       
            % Update the location
            NewX = Solution_Imp(X,BestX,lb,ub,N,cofi,M,A,D,i); 
            
            % Cost function calculation and Boundary check
            [NewX , Sol_CostNew] = Boundary_Check(NewX,fobj,LB,UB);
            
            % Adding new gazelles to the herd
            X=[X; NewX];       %#ok
            Sol_Cost=[Sol_Cost; Sol_CostNew];%#ok
            [~,idbest]=min(Sol_Cost);
            BestX=X(idbest,:);
            
        end
        
        % Update herd
        [Sol_Cost, SortOrder]=sort(Sol_Cost);
        X=X(SortOrder,:);
        [BestFitness,idbest]=min(Sol_Cost);   
        BestX=X(idbest,:);
        X=X(1:N,:);
        Sol_Cost=Sol_Cost(1:N,:);
        cnvg(Iter)=BestFitness;%#ok
        BestF=BestFitness;
    end
end
function cofi = Coefficient_Vector(dim,Iter,MaxIter)
    a2=-1+Iter*((-1)/MaxIter);
    u=randn(1,dim);
    v=randn(1,dim); 
    cofi(1,:)=rand(1,dim);
    cofi(2,:)= (a2+1)+rand;
    cofi(3,:)= a2.*randn(1,dim);
    cofi(4,:)= u.*v.^2.*cos((rand*2)*u);
            
end
function NewX = Solution_Imp(X,BestX,lb,ub,N,cofi,M,A,D,i)
    NewX(1,:)=(ub-lb)*rand+lb;
    NewX(2,:)=BestX-abs((randi(2)*M-randi(2)*X(i,:)).*A).*cofi(randi(4),:);
    NewX(3,:)=(M+cofi(randi(4),:))+(randi(2)*BestX-randi(2).*X((randi(N)),:)).*cofi(randi(4),:);
    NewX(4,:)=(X(i,:)-D)+(randi(2)*BestX-randi(2)*M).*cofi(randi(4),:);
            
end
function [NewX , Sol_CostNew] = Boundary_Check(NewX,fobj,LB,UB)
    for j=1:4
        NewX(j,:) = boundaryCheck(NewX(j,:), LB, UB);
        Sol_CostNew(j,:)=fobj(NewX(j,:));%#ok
    end
            
end
function [ X ] = boundaryCheck(X, lb, ub)
    for i=1:size(X,1)
            FU=X(i,:)>ub;
            FL=X(i,:)<lb;
            X(i,:)=(X(i,:).*(~(FU+FL)))+ub.*FU+lb.*FL;
    end
end