主成分分析

原创于 2025-04-24 12:43:04 发布 · 785 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能

多元统计分析专栏收录该内容

6 篇文章

订阅专栏

一、实验目的

1.理解主成分分析的基本理论与方法;

2.了解主成分的性质;

3.理解主成分的求解方法;

4.掌握用 SPSS软件求解主成分的方法;

5.正确理解软件输出结果并对结果进行分析。

二、实验内容

为掌握我国各地区主要行业的城镇私营企业就业人员的平均工资水平，选取2016年我国30个省、直辖市、自治区（西藏地区数据缺失）9个行业就业人员的平均工资数据（数据来源于2017年《中国统计年鉴》），如表5-1所示。下面我们用主成分分析方法处理该数据，以期用较少的变量描述这些行业各地区就业人员的工资水平。

SPSS 软件中主成分分析与因子分析均在 Factor Analysis 模块中完成。因此，在SPSS数据表中录入以上数据后，依次点击 Analyze→Dimension Reduction--Factor 进人Factor Analysis（因子分析）对话框，然后，将左边的9个变量全部选人Variables框中。点击右侧的Extraction按钮打开相应对话框，其中 Method是 Principal components（主成分），Analyze 部分可以选择是从Correlation matrix（相关阵）还是从Covariance matrix（协方差阵）出发求解主成分，默认是从相关阵出发。本例中各变量的量纲差别不大，为了保留各变量自身的变异，选择从协方差阵出发求解主成分。Display 部分可以选择输出Unrotated factor solution （未旋转的因子解）和Scree plot（碎石图）。Extract部分可以选择提取大于1的特征根与其所对应的主成分或者设定固定的因子（此处为主成分）个数，但是如果 Analyze 选择协方差阵，则会提取大于特征根均值的指定倍数（默认为1）的特征根。点击Continue 继续，再点击OK运行，即可得到输出结果5-1。

输出结果5-1

Communalities
	Raw		Rescaled
	Initial	Extraction	Initial	Extraction
x1	26004055.454	10914931.128	1.000	.420
x2	57695867.620	41390795.022	1.000	.717
x3	50785025.954	22057559.362	1.000	.434
x4	36828663.803	16221258.870	1.000	.440
x5	24024431.289	13044594.919	1.000	.543
x6	450219944.461	425125347.472	1.000	.944
x7	148052260.516	128615863.650	1.000	.869
x8	59560872.516	49311965.237	1.000	.828
x9	80421636.368	61682999.369	1.000	.767
Extraction Method: Principal Component Analysis.

Total Variance Explained
	Component	Initial Eigenvaluesa			Extraction Sums of Squared Loadings
	Component	Total	% of Variance	Cumulative %	Total	% of Variance	Cumulative %
Raw	1	768365315.029	82.302	82.302	768365315.029	82.302	82.302
	2	82685251.724	8.857	91.159
	3	29249216.165	3.133	94.292
	4	17215863.074	1.844	96.136
	5	14296273.991	1.531	97.667
	6	7511072.068	.805	98.472
	7	6169206.857	.661	99.132
	8	5030735.355	.539	99.671
	9	3069823.718	.329	100.000
Rescaled	1	768365315.029	82.302	82.302	5.963	66.253	66.253
	2	82685251.724	8.857	91.159
	3	29249216.165	3.133	94.292
	4	17215863.074	1.844	96.136
	5	14296273.991	1.531	97.667
	6	7511072.068	.805	98.472
	7	6169206.857	.661	99.132
	8	5030735.355	.539	99.671
	9	3069823.718	.329	100.000
Extraction Method: Principal Component Analysis.
a. When analyzing a covariance matrix, the initial eigenvalues are the same across the raw and rescaled solution.

Component Matrixa
	Raw	Rescaled
	Component	Component
	1	1
x1	3303.775	.648
x2	6433.568	.847
x3	4696.548	.659
x4	4027.562	.664
x5	3611.730	.737
x6	20618.568	.972
x7	11340.893	.932
x8	7022.248	.910
x9	7853.853	.876
Extraction Method: Principal Component Analysis.
a. 1 components extracted.

其中，Communalities 表给出了该次分析所保留的前m个主成分从每个原始变量中提取的信息。表中Raw所对应的两列分别表示各原始变量的方差和保留的主成分所提取的差，而Rescaled所对应的两列分别表示将各变量的方差转化为1（除以自身方差）和前个主成分对各原始变量的方差贡献率，例如对 $X_{_1}$ 的方差贡献率为

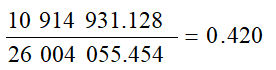
从表中可以看到主成分包含变量 $X_{_6}$ 94.4%的信息，而包含变量 $X_{_1}$ 的信息最少。Total Variance Explained 表给出了主成分解释原始变量总方差的情况。此处，SPSS默认保留大于特征根均值的特征根，本例中仅保留了1个特征根，为768365315.029，它是第一主成分的方差。表中Raw部分显示第一主成分的方差贡献率为82.302%，是保留的特征根占所有特征根的和的比值，由此可见第一主成分解释原始变量总差异的效果比较好。对应的Rescaled 部分所显示的是该主成分对原始各变量方差贡献率的和，即0.420+.717+0.434+0.440+0.543+0.944+0.869+0.828+0.767=5.963，以及该主成分占所有主成分对原始变量方差贡献率总和（等于9)的比值为：5.963/9=0.663。

Component Matrix表给出了可以计算主成分关于原始变量的线性表达式的系数向量在因子分析中被称为因子载荷阵），其中Raw所对应的列向量为 $\gamma _{1}\sqrt{\lambda _{1}}$ ，其中 $\lambda _{1}$ 为协方差阵的第一特征根， $\gamma _{1}$ 为相应的特征向量，Rescaled所对应的列向量是主成分的因子负荷量，即第一主成分 $Y_{1}$ 和 $X _{1}$ ；的相关系数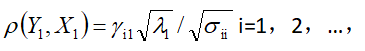9。根据表中的数据，对Raw所对应列的各值求平方和，很容易验证性质4成立；另外，也可以选择保留所有主成分，根据新输出的Component Matrix 表中数据验证性质5，此处不再详达，感兴趣的读者可自行验证。

为写出第一主成分关于原始变量的线性表达式，需要将Component Matrix 表中Raw所对应的列向量除以 $\sqrt{\lambda _{1}}$ ，得到变换系数向量（即特征向量），进而得到第一主成分的表达式为：

三、实验总结

由前面内容知道，可通过因子负荷量来解释主成分成因或原始变量对主成分的重要性。根据Component Matrix表中第一主成分对应的因子负荷量可看到，在第一主成分中占较大比重，说明第一主成分主要综合了第三产业的就业人员的工资水平。

上述结果是从协方差阵出发计算主成分得到的，如果选择从相关阵出发，所有输出结果中会没有Rescaled部分，在后续例题中将会看到。另外，除了按默认设置保留主成分外，我们也可以在Extraction中通过 Fixed number of factors来设定合适的主成分的个数。在实际进行主成分分析时，可以先按照默认设置做一次主成分分析，然后根据输出结果确定应保留主成分的个数，再重新做分析。对于本例，可以选择保留主成分的个数为2，然后再对输出结果进行分析。