链式前向星存图的图操作 模板

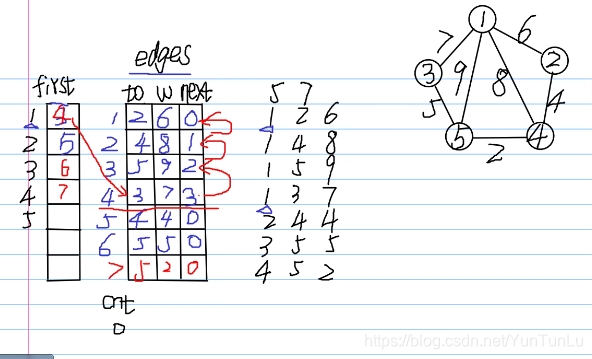
我们存的是边的信息

结构体写法

memset(h, -1, sizeof h);
struct edge{
	//邻接顶点，边权，下一条边
	int to, w, next;
}e[N]; // 所有的边
int h[N]；// 每个顶点链下去的
int tot; // 当前是第几条边了

加边

void add(int a, int b, int w)
{
	e[tot] = edge{b,w,h[a]}; // 头插法
	h[a] = tot++;
}

其中 i != -1 可以写成~i

DFS 复杂度 $O(n+m)$

void dfs(int u)
{
	vis[u] = true;
	for(int i = h[u]; i != -1; i = e[i].next)
	{
		int v = e[i].to;
		if(!vis[v])
			dfs(v);
	}
} 

BFS

void bfs(int u)
{
	queue<int> q;
	vis[u] = true;
	q.push(u);//第一个节点入队 
	while(!q.empty())
	{
		int t = q.front();
		for(int i = h[t]; i != -1; i = e[i].next)
		{
			int v = e[i].to;
			if(!vis[v])
			{
				vis[v] = true;
				q.push(v);
			}
		}
	}
}

拓扑排序 $O(n+m)$

bool topSort()
{
	queue<int> q;
	for(int i = 1; i <= n; i++)
		if(!de[i])
		{
			q.push(i);
			cnt++;
		}		
	while(!q.empty())
	{
		int t = q.front();
		q.pop(); 
		for(int i = h[t]; i !=-1; i++)
		{
			int v = e[i].to;
			if(--de[v] == 0)
			{
				q.push(v);
				cnt++;
			}
		}
	}
	//所有点都入队过了，说明存在。因为队列里的点都是入度为0 
	return cnt == n;
} 

Dijkstra 堆优化 $O（(n+m)logn）$

贪心策略，权值为正。朴素版的dijkstra 对于每个点都要线性遍历一遍，复杂度 $O(m+n^2)$

typedef pair<int,int> pii; 
int n;	//顶点数 
int dist[N];// u 到各点的距离 
bool vis[N];//每个点是否已被确定最短距离
void dijkstra(int u)
{
	memset(dist,inf,sizeof dist);
	dist[u] = 0;
	priority_queue<pii,vector<pii>,greater<pii> > q;
	q.push({0,u}); //first为距离，second为节点 
	while(!q.empty())
	{
		pii t = q.top();
		q.pop();
		
		int ver = t.second;
		//已经更新过了
		if(vis[ver])	continue;
		vis[ver] = true;
		
		for(int i = h[ver];i != -1; i = e[i].next)
		{
			int j = e[i].to;
			if(dist[j] > dist[ver] + e[i].w)
			{
				dist[j] = dist[ver] + e[i].w;
				q.push({dist[j], j});
			}
		}
	}
} 

Bellman-Ford $O(nm)$

注意：权值可为负，但不能包含负环回路。
算法思想：若顶点v1~v2存在最短路，则此路径最多只有 n-1 条边，每个点都枚举了1 ~ n-1轮。
判负环： n-1 轮后，再枚举每条边，如果还能更新成更短的，则存在负权回路。

int n, m;//顶点数，边数 
int dist[N]; // u 到所有点的最短路 
void Bellman-Ford(int u)
{
	memset(dist,inf,sizeof dist);
	dist[u] = 0;
	for(int k = 2; k <= n; k++)//共递推 n-1 轮 
		for(int i = 1; i <= n; i++)//枚举每个点 i 
		{
			for(int j = h[i]; j !=-1; j = e[i].next)//再枚举 i 出发的每条边 
			{
				int p = e[j].to; //松弛操作 
				dist[p] = min(dist[p], dist[i]+e[j].w);
			}
		}		
}

SPFA $O(km)$

算法思想：Bellman-ford的队列优化，不需要算每个点时都要扫描 n-1 次，如果$v1-v2$ 最短路是 n-1 则 v1 到中间点的最短路的长度就已经确定了，所以只用能使距离更短的点更新，在队列里收集起来。
判负环：如果一个顶点入队次数超过 n 次，则存在负环。统计每个顶点入队的次数，在取出头顶点时，判断入队次数是否超过 n 次。

int n, m;//顶点数，边数 
int dist[N]; // u 到所有点的最短路 
int cnt[N]; //每个点入队次数
bool vis[N]; //每个点是否在队列中 
void SPFA(int u)
{
	memset(dist,inf,sizeof dist);
	dist[u] = 0;
	queue<int> q;
	q.push(u);
	vis[u] = true;
	while(!q.empty())
	{
		int t = q.front();
		q.pop();
		vis[t] = false; //每个点都有可能被用到多次 
		for(int i = h[t]; i != -1; i = e[i].next)
		{
			int j = e[i].to;
			if(dis[j] > dist[t] + e[i].w)
			{
				dist[j] = dist[t] + e[i].w;
				if(!vis[j])  //不需要重复加入 
				{
					q.push(j);
					vis[j] = true;
				}
			}
		}
	}
}

Floyd

int dist[N][N],w[N][N];
//初始化
for (int i = 1; i <= n; i++)
  	for (int j = 1; j <= n; j++)
 	{
 	  dist[i][j] = w[i][j];
      if (i == j) 
      	dist[i][j] = 0;
      else 
      	dist[i][j] = inf;
	}
void floyd()
{
    for (int k = 1; k <= n; k++)//中间节点
        for (int i = 1; i <= n; i++) //枚举点对
            for (int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}