如何在3s之内解决17皇后问题

随着LeetCode逐渐被大家熟知，N皇后问题也变得越来越容易了（题号只有51，大部分刷题的人都会刷到），但是LeetCode中的题目规模只到9，所以处理起来不是特别麻烦。18年的时候，楼教主在小马智行的招聘面试中出了一个17皇后的问题，很多人吐槽“出的题好简单，楼教主不刷力扣吗”。不要小看数字17，随着N的增大，N皇后的复杂度会越来越高，时间会以量级的规模上升，我们需要经过很多优化才能使得17皇后的求解速度达到3s以内。

1. 朴素实现

首先介绍最朴素的回溯解法，基本思路就是维护之前所有行皇后的摆放状态，然后去判断当前行哪些位置可以摆放皇后。代码如下：

// 检查之前的row-1行是否有冲突的皇后
bool check(int row, int col, int N, vector<int>& cur) {
	// 判断逻辑就是检查和要摆放的位置是否在相同的列、对角线、斜对角线
    for(int i=0;i<row;i++) {
        if((cur[i]&(1<<col))
                ||((col-row+i>=0)&&(cur[i]&(1<<(col-row+i))))
                ||((col+row-i<N)&&(cur[i]&(1<<(col+row-i))))) {
            return false;
        }
    }

    return true;
}

void dfs(int row, int N, vector<int>& cur,int& sum) {
    if(row==N) {
        sum++; // 除了计数，cur也保留了当前计算出的N皇后结果
        return;
    }
 	// 检查第row行第i列是否可以放置皇后
    for(int i=0;i<N;i++) {
        if(check(row, i, N, cur)) {
            cur[row]|=(1<<i);
            dfs(row+1,N,cur,sum);
            cur[row]^=(1<<i);
        }
    }
}

我的电脑CPU是16核AMD Ryzen 7 5800X，上述代码在3s之内只能跑出14皇后，15皇后运行时间已经到了19s，估计17皇后要跑一二十分钟了。

2. 位运算实现

针对N皇后问题，很早之前matrix67就给我们介绍了一个位运算的优雅解法。我们先给出代码：

void fast_dfs(int cur_row, int N, int row, int left, int right, vector<int>& cur, int& sum) {
    if(cur_row==N) {
        sum++;
        return;
    }

    int pos=((1<<N)-1)&(~(row|left|right)); // 找出所有合法的位置
    while(pos) {
        int p=pos&(-pos); // 遍历每一个合法的位置
        pos-=p;
        cur[cur_row]|=p;
        fast_dfs(cur_row+1, N, row|p, (left|p)<<1, (right|p)>>1, cur, sum);
        cur[cur_row]^=p;
    }
}

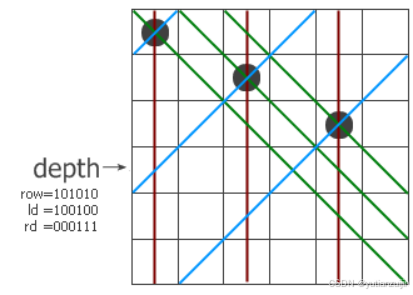
在朴素的回溯解法中，当我们需要检查当前位置是否合法时，我们需要检查之前的每一行来判断是否存在冲突，位运算直接将该检查由O(N)降为O(1)。核心就在于位运算方法使用了三个变量：row，left，right。row表示之前的行中，哪些位置已经放置了皇后；left表示之前行放置皇后的位置左移一位构成的位置，用来表示之前皇后对角线上的位置；right表示之前放置皇后的位置右移一位构成的位置，用来表示之前皇后斜对角线上的位置。通过这三个变量我们就可以知道针对当前位置哪些位置已经是非法位置，而不用再检查之前的每一行。如果还是不太明白可以看一下matrix67博客中的配图，很好地解释了这三个变量的作用。图中，棕色线表示row，蓝色线表示left，绿色线表示right，方格中被划线的位置就是非法的位置。


上述代码可以在大概1s左右完成15皇后的计算，相比朴素的回溯解法快了20倍左右，但是距离快速完成17皇后还有不少距离。上述的位运算解法还保留了cur这个变量，cur变量在朴素解法中是必须的，但是在位运算中除非我们要保留每一个可能的解否则就可以直接去掉。去掉之后代码如下：

void fast_dfs2(int N, int row, int left, int right, int& sum) {
    int limit=(1<<N)-1;
    if(row==limit) {
        sum++;
        return;
    }

    int pos=limit&(~(row|left|right));
    while(pos) {
        int p=pos&(-pos);
        pos-=p;
        fast_dfs2(N, row|p, (left|p)<<1, (right|p)>>1, sum);
    }
}

优化之后的代码会略微变快，但是提升很小。可以看出上面的代码是一个尾递归的实现，我们可以比较方便的用堆栈来将递归优化掉，去掉递归之后的实现如下：

void nodfs(int N,int& sum) {
    int limit=(1<<N)-1;
    stack<tuple<int,int,int>> st;
    st.emplace(0,0,0);

    while(!st.empty()) {
        auto [row,left,right]=st.top();st.pop();
        if(row==limit) {
            sum++;
            continue;
        }
        int pos=limit&(~(row|left|right));
        while(pos) {
            int p=pos&(-pos);
            pos-=p;
            st.emplace(row|p, (left|p)<<1, (right|p)>>1);
        }
    }
}

非递归代码的核心就是用栈来模拟递归，栈中存储的就是row、left、right三个变量。不过不幸的是，上述非递归代码的速度并没有比简化的递归代码快。

3. openmp实现

为了实现更快的速度，我们再从并行的角度来考虑一下如何优化。一个比较容易想到的思路就是把第一行每一个位置的计算分到不同的线程里面去做，因为它们之间没有什么依赖。所以我们可以利用openmp将第一行放在for循环中进行并行。所有线程执行结束之后，汇总每一个位置的结果即是最终的结果。代码如下：

int parallel_n_queens(int N) {
    int sum=0;
    vector<int> partial_sum(N);

#pragma omp parallel for
    for(int i=0;i<(N+1)/2;i++) {
        int row=1<<i;
        fast_dfs2(N, row, row<<1, row>>1, partial_sum[i]);
    }

    for(int i=0;i<(N+1)/2;i++) {
        sum+=partial_sum[i];
    }

    for(int i=0;i<N/2;i++) {
        sum+=partial_sum[N/2-1-i];
    }

    return sum;
}

上述代码除了利用openmp加速之外，还简单考虑了对称性，只计算了第一行一半的位置。16皇后可以在0.4s以内完成，17皇后大概3s左右。当然上述代码还可以进一步优化，优化思路就是将N皇后的第二行也展开，提升代码的并行性，不过感觉实现略微复杂，就留给大家了……
上述几种算法的速度对比如下：

方法	12	13	14	15	16	17
naive	100ms	471ms	2.8s	19s	138s	-
fast_dfs	5ms	28ms	161ms	1s	6.5s	45s
fast_dfs2	3.8ms	22ms	138ms	0.9s	5.9s	40s
nodfs	5ms	28ms	164ms	1s	7.2s	51s
parallel_n_queens	0.7ms	2.5ms	12.5ms	74ms	425ms	3.2s

可以看出，最终并行版本也没有到3s之内，但是我换用同事的13代i9是可以跑到3s之内的，所以最终还是实现了标题说的目标……