Leetcode 850 矩形面积 II

最新推荐文章于 2024-09-27 00:07:40 发布

koishi70

最新推荐文章于 2024-09-27 00:07:40 发布

阅读量2.9k

点赞数 2

分类专栏： Leetcode 文章标签： Leetcode

本文链接：https://blog.csdn.net/yuweiming70/article/details/80639361

版权

Leetcode 专栏收录该内容

34 篇文章 0 订阅

订阅专栏

该博客详细介绍了如何解决LeetCode第850题，即计算轴对齐矩形叠加覆盖后的总面积。通过排序、去重矩形的y坐标，确定每个y区间的矩形，再计算x坐标并集覆盖的长度，最后乘以y区间长度得到总面积。算法简洁高效，适用于处理不超过2^32的矩形叠加面积问题。

摘要由CSDN通过智能技术生成

题目描述：

我们给出了一个（轴对齐的）矩形列表 rectangles 。对于 rectangle[i] = [x1, y1, x2, y2]，其中（x1，y1）是矩形 i 左下角的坐标，（x2，y2）是该矩形右上角的坐标。

找出平面中所有矩形叠加覆盖后的总面积。由于答案可能太大，请返回它对 10 ^ 9 + 7 取模的结果。

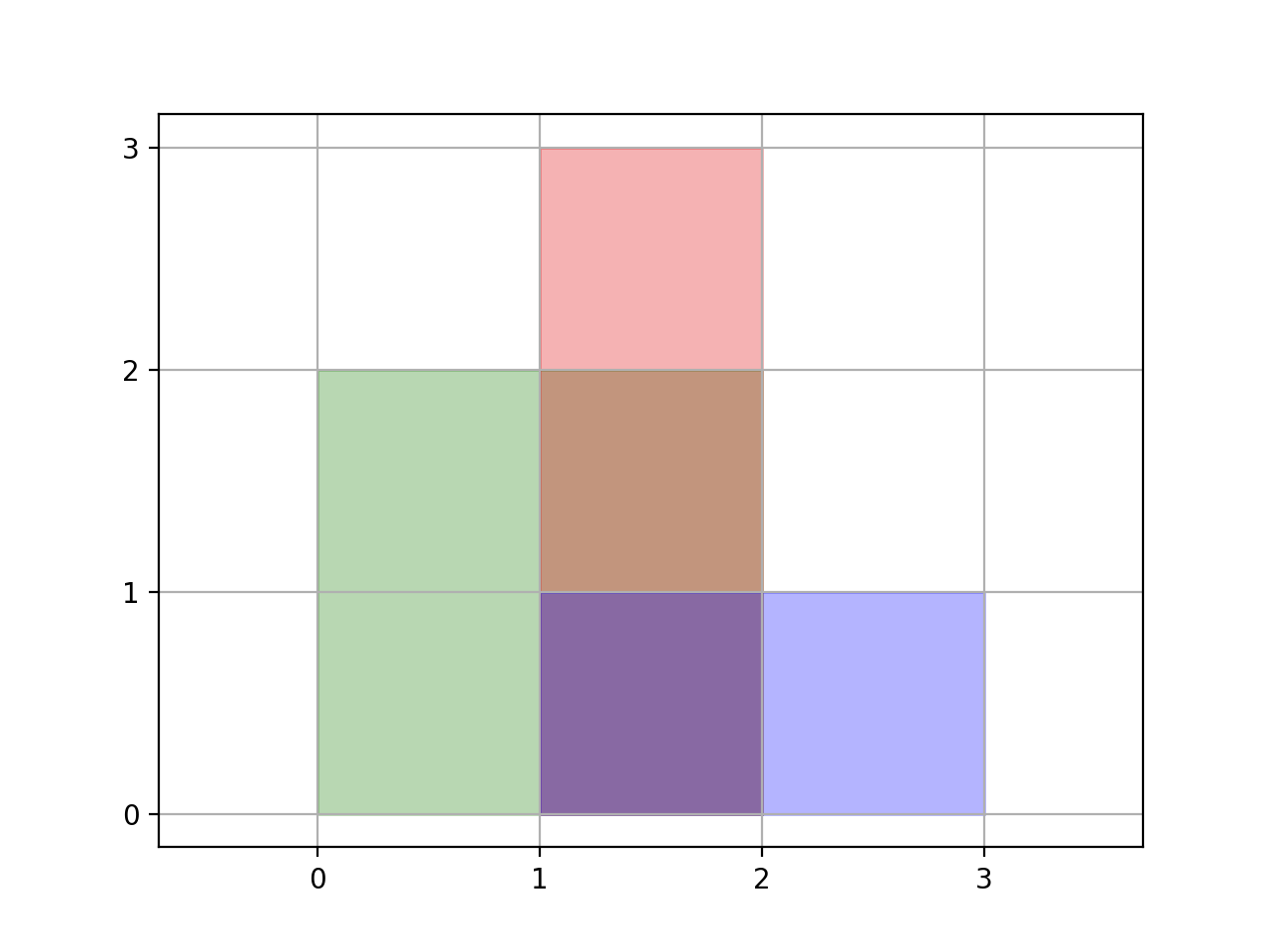
示例 1：

输入：[[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出：6
解释：如图所示。

示例 2：

输入：[[0,0,1000000000,1000000000]]
输出：49
解释：答案是 10^18 对 (10^9 + 7) 取模的结果， 即 (10^9)^2 → (-7)^2 = 49 。

提示：

1 <= rectangles.length <= 200
rectanges[i].length = 4
0 <= rectangles[i][j] <= 10^9
矩形叠加覆盖后的总面积不会超越 2^63 - 1 ，这意味着一个 64 为有符号整数可以用来保存面积结果。

算法：

1.将所有矩形的y1y2收集起来，排序去重，得到一个all_y数组，这个数组就可以指示每一个最小的y间隔是多少。

2.对于每一个最小的y_min:y_max的范围，求出这个范围内有哪些矩形，收集这些矩形的x1x2

3.对于这些x1x2，求出这些x范围的并集所覆盖的长度sum_x

4.sum_x*y小区间的长度，加到答案里面去。

代码：

class Solution {
public:
    long long binji(vector<int> &xs)
    {
        int n=xs.size()/2;
        long long ans=0;
        vector<int> all_x(xs);
        sort(all_x.begin(),all_x.end());
        all_x.erase(unique(all_x.begin(), all_x.end()), all_x.end());//所有的x排序去重，得到了一系列最小的区间
        
        for(int i=0;i<all_x.size()-1;i++)
        {
            int lo=all_x[i],hi=all_x[i+1];//对于一个极小区间来说，遍历一次xs，有的话加上去
            for(int j=0;j<n;j++)
            {
                if(xs[2*j]<=lo && hi<=xs[2*j+1])
                {
                    ans += hi-lo;
                    break;//已经在了，不必算其他的区间
                }
            }
        }
        return ans;
    }
    long long in_delta_y_area(vector<vector<int>>& rectangles,int y_min,int y_max)
        //夹在y一定范围内的矩形的x都要加入一个列表，然后求出这些x的最大最小值
    {
        int n = rectangles.size();
        vector<int> xs;//所有矩形在y范围内的那些x1x2们
        for(int i=0;i<n;i++)
        {
            int x1=rectangles[i][0],y1=rectangles[i][1],x2=rectangles[i][2],y2=rectangles[i][3];
            if(y1<=y_min && y_max<=y2)
            {
                xs.push_back(x1);
                xs.push_back(x2);
            }
        }
        if(xs.size()==0)
            return 0;
        
        long long sum_x =binji(xs);//对于这些x1x2的集合，求出集合并集覆盖区间
        return sum_x*(long long)abs((long long)y_max-(long long)y_min);
    }
    int rectangleArea(vector<vector<int>>& rectangles) 
    {
        int n = rectangles.size();
        vector<int> all_y;//找到所有的y
        for(int i=0;i<n;i++)
        {
            all_y.push_back(rectangles[i][1]);
            all_y.push_back(rectangles[i][3]);
        }
        sort(all_y.begin(),all_y.end());
        all_y.erase(unique(all_y.begin(), all_y.end()), all_y.end());//排序去重，得到最小的y的分割
        
        long long ans=0;
        for(int i=0;i<all_y.size()-1;i++)
            ans += in_delta_y_area(rectangles,all_y[i],all_y[i+1]);//每个y的小区间都求一次x方向上的矩形之和
        
        return ans % 1000000007;
    }
};