时间复杂度与时间限制
时间限制
一般会在题目中给出,常见的限制有 1 / 2 / 5 / 20 1/2/5/20 1/2/5/20 秒 ( s ) (s) (s),有的时候也会用毫秒 ( m s ) (ms) (ms)的形式给出。我们一般会粗略估算计算机一秒钟可以执行 1 0 8 10^{8} 108级别左右的基础运算(加减乘除等)。
假设一道题目时间限制为 1 1 1 秒,现在有两个算法都能实现这道题,根据题目输入的 n n n 的不同:
- 算法 1 1 1 要进行 n 2 n^{2} n2 次运算
- 算法 2 2 2 要进行 10 × n 10 \times n 10×n次运算
那么显然,当 n ≤ 5000 n≤5000 n≤5000 时,两个算法都绰绰有余,而当 n ≤ 1 0 6 n≤10^{6} n≤106 时,第一个算法就没法在时间限制内得到答案,评测结果就会是超出时间限制。
时间复杂度
表示方法
我们一般用时间复杂度这个概念来描述一个算法的耗时,这个概念详细定义比较复杂,可以简单理解为时间复杂度就是基础运算的规模,更准确的定义可以参照下面的扩展阅读部分。
表示时间复杂度的渐进符号有多种:大 Θ \Theta Θ 、大 Ω \Omega Ω 、小 ω \omega ω 、大 O O O 、小 o o o 等等,各自有不同的规则。因为大写字母 O O O比较容易打字和书写,所以经常会杂糅这些概念,用大 O O O符号来描述算法的时间复杂度上限,通常只保留多项式的最高次项,并省略系数。
一些例子
比如上述的算法 1 1 1 与算法 2 2 2,我们通常会用 O ( n 2 ) O(n^{2}) O(n2) 与 O ( n ) O(n) O(n) 来描述。
再比如对于下述代码:
cin >> n;
for(int i = 1; i <= n; i++)
cin >> a[i];
sum = 0;
for(int i = 1; i <= n; i++)
for(int j = i; j <= n; j++)
sum += a[i] * a[j];
cout << sum;
cin >> a[i]; 执行了
n
n
n 次, sum += a[i] * a[j]; 执行了
n
+
(
n
−
1
)
+
.
.
.
+
1
=
n
×
(
n
−
1
)
2
n+(n-1)+...+1=\frac{n\times(n-1)}{2}
n+(n−1)+...+1=2n×(n−1),总的基础运算次数大概是
1
2
n
2
+
1
2
n
\frac{1}{2}n^{2}+\frac{1}{2}n
21n2+21n 次,只保留最高次项并省略常数后就是
O
(
n
2
)
O(n^{2})
O(n2)。
有的时候某个算法在不同情况下时间复杂度不同,比如最坏情况下快速排序算法时间复杂度会很高,因此为了更准确的描述,我们会说快速排序算法的时间复杂度为:最坏情况下
O
(
n
2
)
O(n^{2})
O(n2),随机数据的一般情况下
O
(
n
log
n
)
O(n\text{ log }n)
O(n log n)。
log n \text{log }n log n表示对数,之所以不写底数,是因为我们可以轻松通过换根公式,加一个系数后把底数进行改变,所以 log 10 n \text{log}_{10}\ n log10 n、 log 2 n \text{log}_{2}\ n log2 n、 log n \text{log }n log n 都可以视作 log 2 n \text{log}_{2}\ n log2 n,写作 log n \text{log }n log n。
对数知识是数学中的难点,下面直接给出常见的
n
n
n 对应的
log
2
n
\text{log}_{2}\ n
log2 n,也可以直接通过 <cmath> 库中的log2() 函数得到。

- sort : O ( n log n ) O(n\text{ log }n) O(n log n)
- lower_bound/upper_bound/binary_search : O ( log n ) O(\text{log }n) O(log n)
- priority_queue : .push() O ( log n ) O(\text{log }n) O(log n), .pop() O ( log n ) O(\text{log }n) O(log n), .top() O ( 1 ) O(1) O(1)
- 判断
n
n
n 是否为质数
- 从 2 ∼ n − 1 2\sim n-1 2∼n−1 试除: O ( n ) O(n) O(n)
- 从 2 ∼ n 2\sim \sqrt{n} 2∼n 试除: O ( n ) O(\sqrt{n}) O(n)
- 埃氏筛法:初始化 O ( n log log n ) O(n\text{ log log }n) O(n log log n),初始化后每次查询 O ( 1 ) O(1) O(1)
- 欧拉筛法/线性筛法:初始化 O ( n ) O(n) O(n),初始化后每次查询 O ( 1 ) O(1) O(1)
- 搜索枚举 n n n 个数的子集: O ( 2 n ) O(2^{n}) O(2n)
- 搜索枚举 n n n 的排列: O ( n ! ) O(n!) O(n!)
常见时间复杂度能处理的数据规模
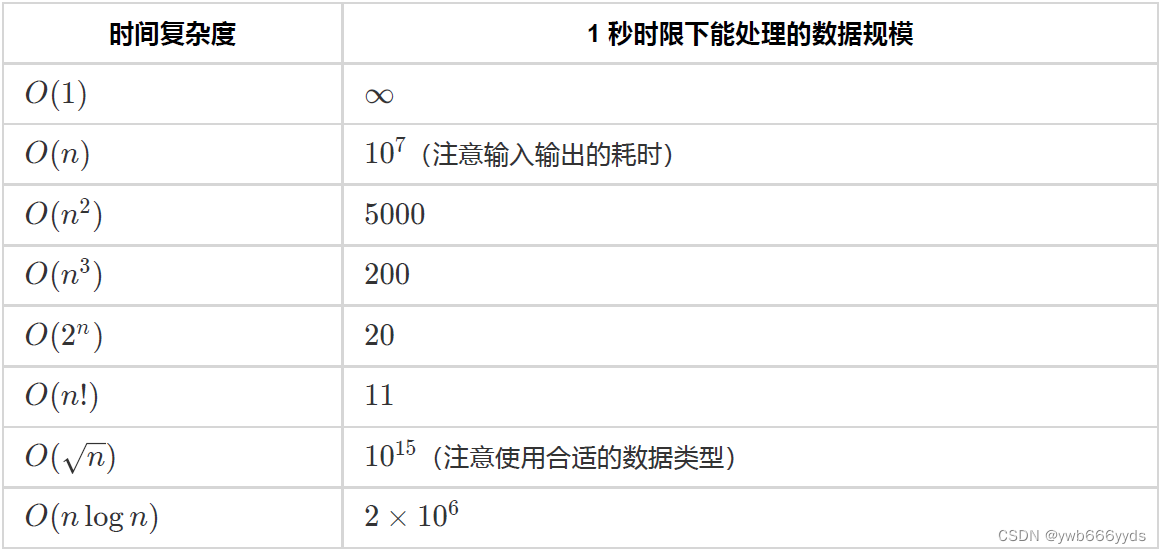
以上描述的都是常见的保险的数据范围,有时也可以通过题目的部分分数据范围反向推测可能用到的算法。
扩展阅读
- OI Wiki, 复杂度:https://oi-wiki.org/basic/complexity/
- 《骗分导论》——李博杰
有错误的地方请指出并修改,谢谢!

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








