牛顿迭代公式(详细)

牛顿迭代公式$X_{n+1}=X_n-\frac{f(x)}{f^{\prime }(x)}$

上网搜了很久,搞懂了一点,简单记录一下

其实弄懂了一点后会发现它并不是很高大上😅

.

先来一段代码

求9的平方根,java实现

public static void main(String[] args) {
        double t = 9;
        while (Math.abs(t-9.0/t)>.001)//牛顿迭代公式 ↓
            t = (9.0/t + t) /2.0; // (a/xn + xn) / 2.0 
        System.out.println(t);
    }
    //

运行结果
3.00009155413138

牛顿迭代公式求平方根并不能算出准确的值,只能无限接近.
	
这里精确度还不是很高,一般情况下是够用了,如果需要更精确,改一下while条件即可.

---

下面来说一下牛顿迭代公式的原理

牛顿法最初由艾萨克·牛顿在《流数法》（Method of Fluxions，1671年完成，在牛顿去世后于1736年公开发表）中提出。约瑟夫·鲍易也曾于1690年在Analysis Aequationum中提出此方法。

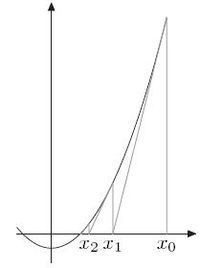
求导

• 首先,我们知道要对哪个数开方,比如现在我们要求出$\sqrt[2]{9}$,那么可以写出 $x^2-9=0$,这一步我想应该没有人看不懂.

  • . . . . . . . . . . . . $f(x)=x^2-9$ . . . . . .
    .

切线

• 然后画出它的二维图形,并作出点$(9,f(9))$处的切线,切线方程可以表示为
  .
  • . . . . . . . . . . . . $y-f(9)=f^{\prime }(9)\ast (x-9)$ . . . . . 切线方程
  • . . . . . . . . . . . . $x=\frac{y-f(9)}{f^{\prime }(9)}+9$
    . . . . . . . . . . . . 当$y=0$时,. . . . . . 我们求到了 $x=5$
    
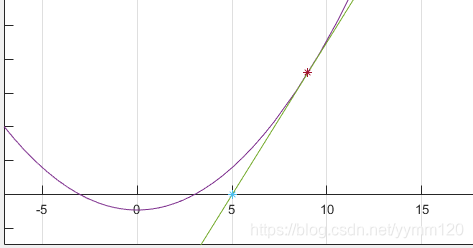
• 我们的目标$\sqrt{9}$的解为3,切线与x轴的交点为5,显然不是答案,我们还得继续做点$(5,f(5))$的切线

再切

• . . . . . . . . . . . . $y-f(5)=f^{\prime }(5)\ast (x-5)$ . . . . . .切线方程
• . . . . . . . . . . . . $x=\frac{y-f(5)}{f^{\prime }(5)}+5$
• . . . . . . . . . . . . 同样,当 $y=0$ 时,$x=3.\ast$, . . . . . .还得继续…

继续切

已经很接近了.,就不继续切线了,

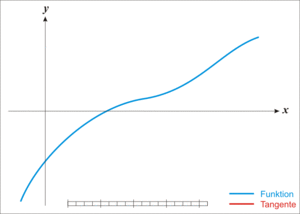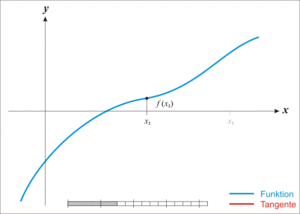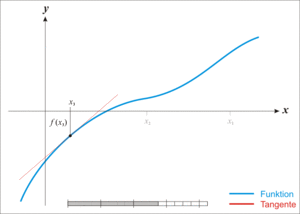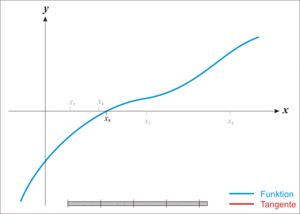
回顾一下,

$f(x)=x^2-a$
$f^{\prime }(x)=2x$
$x_{n+1}=\frac{y-f(x_n)}{f^{\prime }(x_n)}+x_n$ ,

当$y=0$ 时,

$X_{n+1}=-\frac{f(x)}{f^{\prime }(x)}+x_n$ . . . . . . . . . . . . . . . .牛顿迭代公式

化简一下
$X_{n+1}=-\frac{x_n^2-a}{2x_n}+x_n$

最后得到
$X_{n+1}=(\frac{a}{x_n}+x_n)\ast \frac{1}{2}$

以上就是牛顿迭代求平方根的过程了😅

写成java代码上面的样子
//

//

//

.总结一下:

1. $f(x)$求导,
2. 作$k=f^{\prime }(x)$切线,
3. 求出$y=0$时的$x$的值, 赋值$x_1$
4. 作$k=f^{\prime }(x_1)$切线
5. 求出$y=0$时的$x_1$的值,赋值$x_2$
6. 作$k=f^{\prime }(x_2)$切线
7. …

.

参考:
这个动态图易懂
维基百科-牛顿法

.
.
.
.