poj 1942 Paths on a Grid (求组合数)

题目链接

POJ1942

题目大意

在一个尺寸为N*M的网格中（N,M均为无符号32位整数），求从网格左下角走到网格右上角有几种走法，如下图为两种符合要求的走法：

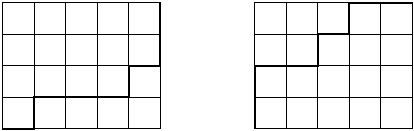
分析

看到这道题会想用递推去做，但这里n与m都很大，用递推无论是时间复杂度还是空间复杂度都不能实现。
再仔细思考，不难发现，每一种方案中，都是n步向上走，m步向右走，即总步数确定，不一样的只是’右’和’上’出现的相对顺序。那么这个问题就相当于在n+m个位置中我取n个位置来放’上’这张卡片的方案数，即求$C_{n+m}^n$或$C_{n+m}^m$。
接着就是要解决如何求组合数的问题，由于这里n,m很大，不能再用杨辉三角的递推关系去求，而要利用组合数的阶乘公式：

$$C_n^m=\frac{n!}{m!(n-m)!}$$
下面总结用一种计算组合数的高效方法：
其实就是用我们平时笔算组合数 $C_n^m$的简便方法： 将n!与(n-m)!中的公因子进行约分，可以发现分子为n向下逐一递减的m项，分母为m!（也为m项），这样便能将时间复杂度控制在O(n-m)。这里涉及除法运算，因此用double储存数据，那么最后要转化为 无符号整型 时就要处理精度问题，有两种方法： 四舍五入+强制类型转换 或者用 setprecision()函数 。

代码

若用setprecison()函数处理精度

#include <iostream>
#include <cmath>
#include <iomanip>  //setprecision()必要头文件
using namespace std;
double comp(unsigned int n,unsigned int m)//求nCm
{
    m=min(m,n-m); //计算优化：将上标化小
    double ans=1.0;
    while (m>0)
        ans*=double(n--)/double(m--);
    return ans;
}
int main()
{
    unsigned int n,m;
    while (cin>>n>>m)
    {
        if (!n&&!m) break;
        cout<<fixed<<setprecision(0)<<comp(n+m,m)<<endl;//记住这句话格式,用该函数会自动四舍五入保留相应位数
    }
    return 0;
}

若用四舍五入+强制类型转换
对应计算组合数的函数如下

unsigned int comp(unsigned int n,unsigned int m)//求nCm
{
    m=min(m,n-m); 
    double ans=1.0;
    while (m>0)
        ans*=double(n--)/double(m--);
    ans+=0.5;//double转unsigned会强制截断小数，必须先四舍五入
    return (unsigned)ans;
}