4月19日-4月25日周报

最新推荐文章于 2024-07-12 16:16:27 发布

YoujinZ

最新推荐文章于 2024-07-12 16:16:27 发布

阅读量1.7k

点赞数 30

文章标签： python

本文链接：https://blog.csdn.net/z12921/article/details/137978184

版权

一、论文阅读部分：GeoUDF: Surface Reconstruction from 3D Point Clouds via Geometry-guided Distance Representation

1.1前提知识了解：

SDF（有符号距离场）：有符号距离场（Signed Distance Field，简称SDF）是一种用来描述物体表面的数学模型。在三维空间中，SDF可以表示每个点到最近的表面的距离，并且考虑了方向，即表面内部的点到表面的距离为负值，表面外部的点到表面的距离为正值。

marching Cube（MC） algorithm: 利用有符号距离场确定边界像素cube

orinented point samples: "oriented point samples"指的是具有方向信息的点样本。在三维空间中，点由其位置坐标以及可能的法线或方向信息组成。这种信息通常用来描述点所在曲面或物体的几何特征，比如法线可以指示曲面的朝向。

Point Cloud Implicit Field（点云隐式场）: 点云隐式场（Point Cloud Implicit Field）是指通过对点云数据进行学习或建模，得到一个隐式函数，该函数可以描述点云所表示的物体表面或几何结构。这个隐式函数通常是基于点云中的点位置以及可能的法向信息进行建模的。

1.2论文阅读：

引言

点云表面重建是三维视觉、图形和机器人技术中一个基本且具有挑战性的问题。传统方法，如泊松曲面重建，通过求解泊松方程来计算占用或有符号距离场（SDF），从而产生稀疏线系统。然后，他们利用移动立方体（MC）算法提取等值面作为重建的网格。这些方法计算高效、可扩展、对噪声具有很好的鲁棒性。但是，它们仅适用于定向点样本。深度学习的最新发展表明，隐式场，如二元占用场（BOF）和有符号距离场（SDF），可以直接从原始点云中学习，这使它们成为一种从无定向点样本重建表面的有前途的工具。

本篇论文介绍了一种基于学习的方法，即GeoUDF，以解决从稀疏点云重建离散表面这一长期存在且具有挑战性的问题。具体来说，提出了一种用于 UDF 及其梯度估计的几何引导学习方法，该方法将查询点的无符号距离显式表示为其到表面上相邻点切平面的距离的可学习仿射平均值。此外，通过显式学习每个点的二次多项式来模拟输入点云的局部几何结构。这不仅有助于对输入稀疏点云进行上采样，而且还自然地诱导了无定向法线，从而进一步增强了 UDF 估计。最后，为了从预测的UDF中提取三角形网格，提出了一个定制的基于边的行进立方体模块。

技术贡献

本文中主要的技术贡献如下：

基于学习的准确、紧凑、高效、可解释的新型UDF及其梯度估计解耦方法;
一种简洁而有效的基于学习的点云上采样和表示方法;
从任何无符号距离场中提取三角形网格的通用方法。

如下图所示是geoudf工作的整个流程：

图一 GeoUDF的流程

方法介绍

Local Geometry Representation（局部几何表示）

设 $P=\{p_{i}\in R^{3}\}_{i=1}^{N}$ 从要重建的曲面 S 采样的 N 个点的输入稀疏点云。微分几何中曲面的局部理论[14]表明，正曲面任何点的局部几何由刚性运动的第一和第二基本形式唯一决定，并且可以表示为二次函数。因此，我们使用多项式来近似以每个点为中心的局部斑块：

$f_i(u)=p_i+A_iE(u)$ , (1)

其中 u = [u1， u2] T ∈ $R^{2}$ 是二维局部参数域中的坐标，E（u） := [1 u1 u2 ${u_{1}}^{2}$ u1u2 ${u_{2}}^{2}$ ] T ∈ $R^{6}$ ， $A_{i}$ ∈ $R^{3*6}$ 是系数矩阵。

我们可以从预定义的局部参数化 $D=[-\delta ,\delta ]^{2}\subset R^{2}$ 中均匀采样 M 二维坐标，然后将其代入方程（1）以在 $p_i$ 周围生成额外的 M 个三维点，产生密集的点云 $P_{M}=\{p_{j}\in R^{3}\}_{j=1}^{N M}$ （2）诱导 $P_{M}$ 的无取向法向量。根据微分几何性质[2]，我们可以计算PM各点的无定向法向量，具体来说，设 $P_{i,m}=f_{i}(u_{m})$ 为PM的一个点， $J_{i,m}=[{\frac{\partial f_{i}}{\partial u_{1,m}}},{\frac{\partial f_{i}}{\partial u_{2,m}}}]$ 为 $p_{i,m}$ 处 $f_i$ 的雅可比矩阵，则其无定向法向量可以通过以下方式计算

$n_{i,m}=\frac{\frac{\partial f_i}{\partial {u1,m}}\times \frac{\partial f_i}{\partial {u2,m}}}{\left | \left | \frac{\partial f_i}{\partial {u1,m}}\times \frac{\partial f_i}{\partial {u2,m}} \right | \right |}$ , (2)

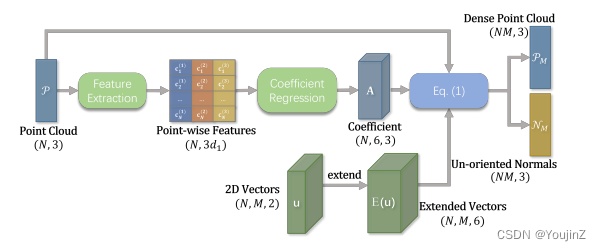
最后，推导的正态向量构成一个集合，表示为 $N_M=\{n_j|n_j\in R^3,\left | \left | n_j \right | \right |=1\}_{j=1}^{N M}$ .其具体实现如下图：

图2 LGR的模块流程图

如图 2 所示，该子网以数据驱动的方式实现该表示过程，归结为预测系数矩阵 $\{A_i\}_{i=1}^N$ 。具体而言，我们采用能够捕获点云数据结构信息的三层EdgeConvs，将P嵌入到高维特征空间中，在第l层生成逐点特征 $\{c_i^{(l)}\in R^{d1}\}_{i=1}^{N}$ 。然后，我们将三层的特征连接起来，并将它们输入到MLP中，以预测18维向量，这些向量被进一步重塑为 $\{A_i\}_{i=1}^N$ 。

Geometry-guided UDF Estimation（几何引导的UDF估计）

该模块旨在估计 $P_M$ 的无符号距离场，其中值为零的等值面表示表面。如前所述，现有的基于学习的UDF估计方法，如NDF和GIFS ，利用神经网络隐式地将UDF从点云回归，从而限制了它们的准确性。此外，经过训练的模型往往泛化性不好。与基于回归的方法形成鲜明对比的是，GUE 利用了输入点云固有的几何特性，从而实现了更准确的 UDF 估计方法，并具有更好的泛化性。

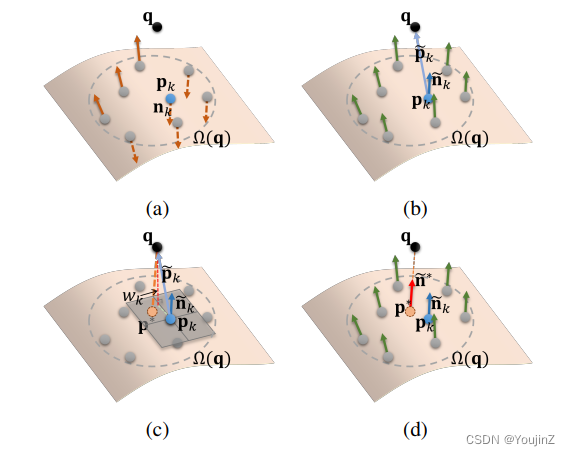
图3 UDF 及其梯度估计过程的图示

给定一个查询点 $q\in R^3$ ，我们可以在欧几里得距离意义上找到其离 $P_M$ 最近的 K个点，表示为 $\Omega (q)=\{p_k|p_k\in R^3\}_{k=1}^K$ 。用 $n_k$ 表示 $p_k$ 的未定向法线。在计算 UDF 之前，如上图 3b 所示，我们首先将 $\{n_k\}_{k=1}^K$ 与 q 通过下面的公式对齐:

$\tilde{n_k}=sgn(<n_k,\tilde{p_k}> )n_k$ , (3)

其中 $\tilde{p_k}:=q-p_k$ ， 〈·， ·〉 计算两个向量的内积，sgn（·）提取输入的符号。方程（3）将 $\tilde{n_k}$ 和 $\tilde{p_k}$ 对齐，即< $\tilde{n_k}$ , $\tilde{p_k}$ 〉 >0。

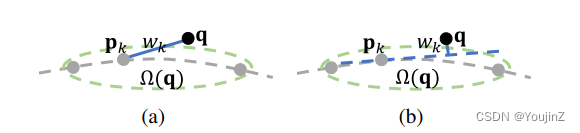
图4 当 $\Omega (q)$ 稀疏时，(a)P2P 和 (b) P2T 距离对比

用 $p^*$ 表示曲面 S 上最接近 q 的点, $\tilde{n^*}$ 表示其对齐的法向量。由于 $\Omega (q)$ 通常覆盖图 3c 所示的一小块区域，我们可以简单地采用 q 和 { $p_k$ } 之间的欧几里得距离的加权平均值，即点对点（P2P）距离，来近似 q 的 UDF：

$U(q)\approx \sum_{p_k\in \Omega (q)}w_1(q,p_k)\cdot \left \| \tilde{p_k} \right \|_2$ , (4)

其中权重 $\{w_1(q,p_k)\}_{k=1}^K$ 非负且满足 $\sum_{k=1}^{K}w_1(q,p_k)=1$ 。然而，尽管进行了上采样， $\Omega(q)$ 可能仍然稀疏，并且q到每个 $p_k$ 的距离远大于其无符号距离值，如上图4a所示，导致较大的近似误差。相反，我们建议通过欧几里得距离的加权平均值来近似 U（q）从 q 到 { $p_k$ } 的每个切平面，即点切平面（P2T）距离：

$U(q)\approx \Phi (q):=\sum_{p_k\in \Omega (q)}w_1(q,p_k)\cdot <\tilde{n_k},\tilde{p_k}>$ , (5)

类似地，我们建议使用曲面法向量的连续性属性和事实来近似 U（q）的梯度，表示为 ∇U（q）。请参见图3d。我们使用 ̃nk，每个都在 ̃n ∗ 左右，将近似 ∇U（q）为

$\bigtriangledown U(q)\approx \Theta (q):=\frac{\sum_{p_k\in\Omega (q)w_2(q,p_k)\cdot \tilde{n_k}}}{\left \| \sum_{p_k\in\Omega (q)w_2(q,p_k)\cdot \tilde{n_k}} \right \|}$ , (6)

其中权重 $\{w_2\}_{k=1}^K$ 为非负且满足 $\sum_{k=1}^{K}w_2(q,p_k)=1$ 。

基于上述公式，将UDF估计问题归结为得到 $\{w_1(q,p_k),w_2(q,p_k)\}_{k=1}^K$ 。如图 5 所示，我们构建了一个子网来自适应地学习它们。直观地说，权重的值应该与 q 和 $p_k$ 之间的相对位置以及 $\Omega (q)$ 的整体形状相关。因此，我们通过 MLP g1（·）嵌入 $\tilde{p_k}$ 和 $\tilde{n_k}$ 来获得所有邻近点的逐点特征，然后将其最大池化，从而产生全局特征 $F_k$ (q)，以编码 $\Omega (q)$ 的整体形状。

$F_k(q)=g_1(\tilde{p_k}\bigoplus \tilde{n_k}), F_q=MaxPool(\{F_k\}_{k=1}^K),$ (7)

其中 ⊕ 代表串联运算符。然后，我们将逐点特征和全局特征（即 $F_k(q)$ 和 $F_q$ ）与 $\tilde{p_k}$ 和 $\tilde{n_k}$ 连接起来，进一步输入到另外两个单独的 MLP（表示为 h1（·）和 h2（·），然后进行 softmax 运算，以预测权重 $\{w_1(q,p_k),w_2(q,p_k)\}_{k=1}^K$

$e_1(q,p_k)=h_1(\tilde{p_k}\bigoplus \tilde{n_k}\bigoplus F_k(q)\bigoplus F(q))$ ,

$e_2(q,p_k)=h_2(\tilde{p_k}\bigoplus \tilde{n_k}\bigoplus F_k(q)\bigoplus F(q)),$

$w_1(q,p_k)=SoftMax(\{e_1(q,p_k)\}_{k=1}^K)$ ,

$w_2(q,p_k)=SoftMax(\{e_2(q,p_k)\}_{k=1}^K)$ (8)

下面是整体网络图:

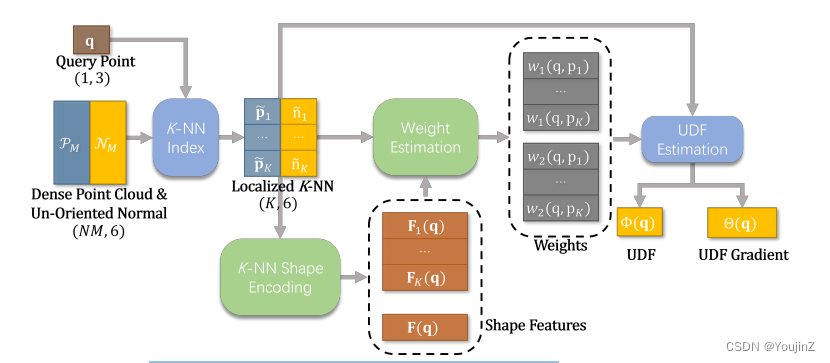
图5 GUE模块流程图

Edge-based Marching Cube（基于边的移动立方体算法）

这部分还在理解

二、代码复现部分：

2.1环境配置

pytorch             #1.10.0+cu111
pytorch3d           #0.6.2
open3d
trimesh
point-cloud-utils

2.1.1创建conda环境

conda create -n geoudf python=3.8
conda activate geoudf

2.1.2 配置 pytorch #1.10.0+cu111

直接使用conda install 或者是用pip install都无法安装成功，使用国内源下载找不到对应版本，最终使用官方的镜像源下载成功，即在python 3.8环境下执行

pip install torch==1.10.0+cu111 torchvision==0.11.1+cu111 torchaudio==0.10.0 -f https://download.pytorch.org/whl/cu111/torch_stable.html

2.1.3 配置 pytorch3d #0.6.2

和上面的问题相同，直接使用pip install 或者conda install找不到对应版本，使用镜像源也无法下载成功，最终在github源码地址https://github.com/facebookresearch/pytorch3d/releases找到对应版本并下载解压后在conda环境下执行以下命令

cd pytorch3d-0.6.2
pip install -i https://pypi.mirrors.ustc.edu.cn/simple/ .

YoujinZ

关注

30
点赞
踩
30

收藏

觉得还不错? 一键收藏
1
评论
4月19日-4月25日周报

设从要重建的曲面 S 采样的 N 个点的输入稀疏点云。微分几何中曲面的局部理论[14]表明，正曲面任何点的局部几何由刚性运动的第一和第二基本形式唯一决定，并且可以表示为二次函数。因此，我们使用多项式来近似以每个点为中心的局部斑块：其中 u = [u1， u2] T ∈是二维局部参数域中的坐标，E（u） := [1 u1 u2u1u2] T ∈∈是系数矩阵。我们可以从预定义的局部参数化中均匀采样 M 二维坐标，然后将其代入方程（1）以在周围生成额外的 M 个三维点，产生密集的点云。
复制链接

扫一扫