第五章 关系

前提知识

整除关系需满足 除数,被除数,商都是整数 (0,-3也属于整数)
A整除B(A/B)=商(), 余数是0 ,而A是被除数,B是除数
小于等于关系L_A ,整除关系D_A

什么是二元关系

令A为某大学所有学生的集合,B表示该大学开设的所有课程的集合,则AxB可表示该校学生选课的所有可能情况.而真正的选课情况则会是AxB的某一个子集

令F为某地所有父亲的集合,S表示该地所有儿子的集合,则FXS可表示父子关系的所有可能情况,而真正的父子关系则会是FxS的某一个子集

二元关系定义

设A,B为两个非空集合,称AxB的任意子集R为从A到B的一个二元关系,简称关系
其中 A称为关系R的前域 , B称关系R的后域 ,如果A=B,则称R为A上的一个二元关系

二元关系的数学符号

若有序对/序偶<x,y>∈R, 通常把这一切事实记作xRy , 读作"x对y有关系R"
反之X对y没有关系R

枚举二元关系

幂集: 集合内的若有n个元素,则排列0元子集,一元子集,二元子集…n元子集
而二元关系是笛卡尔积的子集,若要求求出所有的二元关系,则需要先求出笛卡尔积,再进行幂集排序

空关系 &全域关系& 恒等关系

E_A ={<x,y>|x∈A ∩ y∈B}= A x A
I_A= { <x,x>|x∈A }

举例 集合 A={1,2}
E_A=AxA ={<1,1>,<1,2>,<2,1>,<2,2>}
I_A={<1,1>,<2,2>}

定义域和值域

设R是从A到B的二元关系, 则A为关系R的前域, B为关系R的后域.
令C={x|x∈A, ∃y∈B, <x,y>∈R}, D={y|y∈B, ∃x∈A , <x,y>∈R}
称C为R的定义域,记作C=domR , D为R的值域, 记作D=ranR
R的域: fldR(域)= (定域U值域) domR U ranR

例子

比如X={1,2,3},在X上有关系R={<1,1>, < 3,2>}
则定义域domR 是{1,3}       [ 定义域是将每个关系的第一元素拿出来]
则值域ranR是{1,2}       [ 值域是将每个关系的第二元素拿出来]

而域fldR是{1,2,3}

关系的性质

(1)自反性与反自反性

设R为A上的关系
(1)若∀_x x∈A → <x,x>∈R,则称R在A上是自反的
可以理解成∀_x,有xRx
(2)若∀_x x∈A → <x,x>∉R,则称R在A上是反自反的
可以理解成∀_x,有x和x没有关系R

若R是自反的,则推出R不是反自反的;
若R是反自反的,则推出R不是自反的

自反关系: A上的全域关系E_A, 恒等关系I_A ,小于等于关系L_A,整除关系D_A
反自反关系: 实数集上的小于关系,幂集上的真包含关系

举例

若A={1,2,3},R1,R2,R3是A上的关系,以下判断的自反性质

R1 = {<1,1>,<2,2>} , 是自反的,不是反自反的
因为左式代表<3,3>不存在关系,则与<x,x>是自反的关系,相违背。
则称R1不是自反的,又因<x,x>不存在关系称为反自反的,则推导出R1也不是反自反的

R2 = {<1,1>,<2,2>,< 3,3>,<1,2>}，是自反的,不是反自反的
因为自反的关系都存在，

R3= {<1,3>} 不是自反的,是反自反的
,因为<x,x>不存在关系

(2)对称性与反对称性

设R为A上的关系
(1)若(∀<x,y>)(<x,y>∈R →<y,x>∈R),则称R在A上是对称的
可以理解成 若 ∀<x,y>有xRy 则 yRx

(2)若(∀<x,y>)(<x,y>∈R 且<y,x>∈R → x=y ),则称R在A上是反对称的
可以理解成 若 ∀<x,y>有xRy且 yRx, 则x=y

对称关系: A上的全域关系E_A , 恒等关系I_A 和 空关系Ø
反对称关系: 恒等关系I_A, 空关系Ø

举例
若A={1,2,3},R1,R2,R3是A上的关系,以下判断的对称性

R1 = {<1,1>,<2,2>} 是 对称的,是反对称的
因为左式<1,1>,右式<1,1>都是T,则称<1,1>是对称的 ,同理<2,2>也是对称的
因为左式<1,1>,<1,1>成立T,且1=1,则称<1,1>是反对称的 ,同理<2,2>也是反对称的

R2 = {<1,1>,<1,2>,<2,1>}， 是对称的,不是反对称的
因为<1,1>是对称的, <1,2>可以推导<2,1>.则是对称的
因为<1,1>是反对称的, 左式<1,2>且<2,1>成立T,但1≠2,则不是对称的

R3= {<1,2>,<1,3>} ,不是对称的,是反对称的
因为<1,2>不能推导<2,1>则T蕴含F,则<1,2>不是对称的,同理<1,3>也不是对称的
因为<1,2>且<2,1>不存在关系,则左式为F,则是反对称的,同理<1,3>是反对称的

R4= {<1,2>,<2,1>,<1,3>} 不是对称的,不是反对称的

(3)传递性

定义 设R为A上的关系,若(∀<x,y>)(∀<y,z>) (<x,y>∈R ⋀ <y,z>∈R→ <x,z>∈R ),则称R是A上的传递关系

可以理解成 若 xRy 且yRz ,则xRz

A上的全域关系E_A ,恒等关系I_A , 空关系Ø,
小于等于关系,小于关系,整除关系,包含关系,真包关系

举例
若A={1,2,3},R1,R2,R3是A上的关系,以下判断的传递性

R₁={<1,1>,<1,2>} 是传递的

R₂={<1,2>,<2,3>} 不是传递的
因为不存在<1,3>所以为F, T(<1,2>且<2,3>)蕴含F<1,3>,则不是传递的

R₃={<1,3>} 是传递的
因为左式为F ,则是传递的

关系的性质矩图

证明自反性与对称性与传递性

关系的表示

关系是一个特殊的集合,因此集合的 两种基本表示法(枚举法和叙述法)可以用到关系的表示中

枚举法&叙述法表示例子

关系的图形表示

关系矩阵方式

关系矩阵内的1,0数学意义:      1表示A和B有关系;0表示A和B没关系
1代表A到B有关系R, 0代表A到B没有关系R

关系的运算

集合是父类,关系是子类
关系是一种特殊的集合,因此集合所有的基本运算(交,并,差,补)
都可以应用到关系中,并且同样满足集合的所有运算定理

(1) 布尔矩阵的并和交运算

(2)关系矩阵的布尔运算

理解: 最右边 A与B的积运算的第一排的第一列是1 ,求法是左边A第一排和B第一列中,若存在 1 1对应则,结果为1,否则为0
1 0 1
0 0 1 = 1

---

(3)关系的并交差补运算

(4)关系的复合运算定义

复合运算的关系图法/关系矩阵

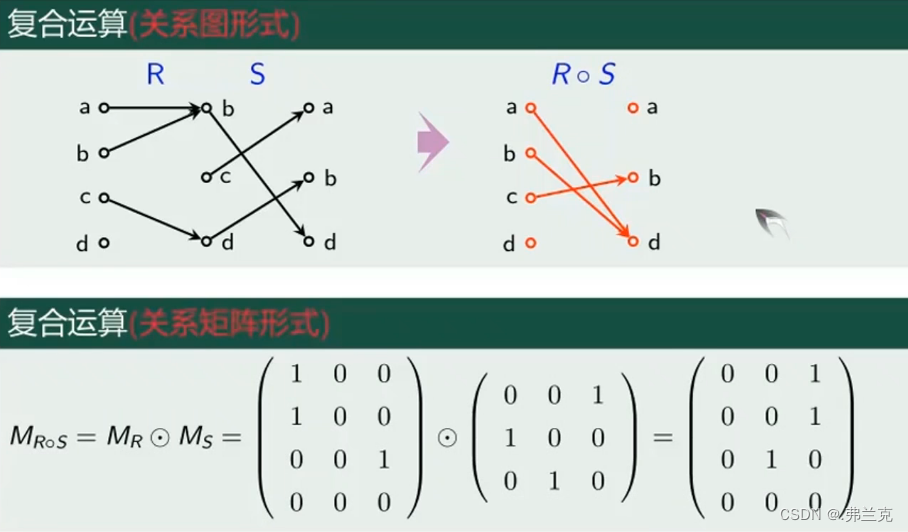
总结 (关系的复合运算)

关系的复合运算公式

注意: R∘ S ≠ S ∘ R
(R∘ S) ∘ T = R ∘ (S ∘T)
(F ∘ G) ^-1 = G ^-1 ∘ F ^-1
M_R∘S = M_R ⨀ M_S

1.结合律

2.分配律

(5)关系复合逆运算定义

(6)关系的逆运算定理

I.  R的关系图中,改变箭头方向即得R ^-1的关系图,
II.  R与R ^-1 的关系互为转置矩阵(就是行和列互换)
III.  R^-1 的定义域和值域正好是R的值域和定义域
IIII.  domR = ranR ^-1 , ranR = domR^-1
|||||.   |R|=|R ^-1|

逆运算公式

定理 设R和S是集合A到B的二元关系,则⋃⋂ ⋁⊆
(1)M_R⋂S = M_R ⋀ M_S
(2)M_R⋃S = M_R ⋁ M_S
(3)若R⊆S,则R^-1 ⊆ S^-1
(4)若R⊆S,则R^c ⊆ S^c(c表示的是R的补集=E_A-S=AxB-S)
(5)(R ⋂ S)^-1= R^-1 ⋂ S^-1
(6)(R ⋃ S)^-1= R^-1 ⋃ S^-1
(7)(R ⋂ S)^c= R^c ⋃ S^c (和德摩根定律类似 ~(A⋂B)= ~A ⋃ ~B )
(7)(R ⋃ S)^c= R^c ⋂ S^c (和德摩根定律类似 ~(A⋃B)= ~A ⋂ ~B )

(7)关系的幂运算

因为 I A o R = R = I B o R, R⁰⁺¹ =R⁰ +R¹ ,得R⁰= I A

幂的性质

幂运算的收敛性

关系的闭包

定义设R是非空集合A上的关系,R的自反(对称/传递)闭包R₁满足以下条件

1.增加条件后,自反闭包R₁是自反的
2.关系R⊆自反闭包R₁
3.对于A上包含R的自反关系R₁₁ ， 有R₁⊆R₁₁，

则将R的自反闭包记作 r(R）,一般称R的自反闭包记作r( R),
对称闭包 记作 s( R)
传递闭包 记作 t( R)
或者称:自反闭包包含R的最小的自反关系,就叫做自反闭包

关系闭包的公式

1. r( R) = R⋃ I_A
2. s( R) = R⋃ R^-1
3. t( R) = R⋃ R²⋃ R³⋃ R⁴⋃ R⁵⋃ R⁶…⋃ Rⁿ

等价关系与序关系

前提

等价关系是特殊的二元关系序偶的集合
A上的关系R的等价关系构成的集合是集合A的子集

举例

设A={1,2,3},确定A的所有划分
注:π是划分关系的集合

π₁= { {1},{2},{3}} ,它的划分块是3
π₂= { {1,2},{3}} , 它的划分块是2
π₃= { {1},{2,3}} , 它的划分块是2
π₄= { {1,3},{2}} , 它的划分块是2
π₅={A} , 它的划分快是1

共有五种划分方式

等价关系与商集

定义1

设R为非空集合上的关系,若R是自反的,对称的,传递的,则称R为A上的等价关系.
设R是一个等价关系,若<x,y>∈R,称x等价于y 记作x~y

定义2

设R为非空集合A上的等价关系,令x∈R,[x]_R= {y|y∈A ⋀ xRy },称[x]_R为x关于R的等价类,简称为x的等价类,简记为[x]
理解来说: 在等价关系R下,与x的有关系的其他元素,包括他自己,构成的一个集合,就叫做x的等价类

定理

设R设非空集合A上的等价关系,则
(1)∀ x ∈ A ,[x]是A的非空子集.
(2)∀x,y∈A,如果xRy,[x]=[y]
(3)∀x,y∈A,如果x和y没有关系R,则[x]≠[y]
U{ [x]| x∈A} = A,即所有等价类的并集就是集合A

商集的定义

设R为非空集合A上的等价关系,以R的所有等价类作为元素的集合称为R的商集S,记作A/R
A/R ={ [ [x]_R | x∈A }

比如集合A={1,2,3,4,5,6,7,8},x和y取余3相等的等价关系R={<1,1>,<1,4>,<1,7>,<4,1>,<7,1>,<4,7>,<7,4>,<4,4>,<7,7>.<2,2>,<2,5>,<5,2>,<5,5>,<2,8><8,2>,<5,8>,<8,5>,<8,8>,< 3,3>,< 3,6>,<6,3><6,6>}
A/R = { [1]_R , [2]_R , [3]_R }

举例1

A mod B = A取余B

[1]=[4]=[7]={1,4,7} ,表示 1mod 3 = 4mod3 = 7mod 3 ,余数都是1
[2]=[5]=[8]={2,5,8} 2mod 3 = 5mod3 = 8mod 3 ,余数都是2
[3]=[6] 3mod3 = 6 mod 3,余数都是0

举例2
设X= {1,2,3,4},X的划分S={ {1} , {2,3} , {4} },试写出S导出的等价关系R
R={ <1,1> , <2,2>,<2,3>,< 3,2>,< 3,3>, <4,4> }