一、PCA:
principal component analysis
主成分分析
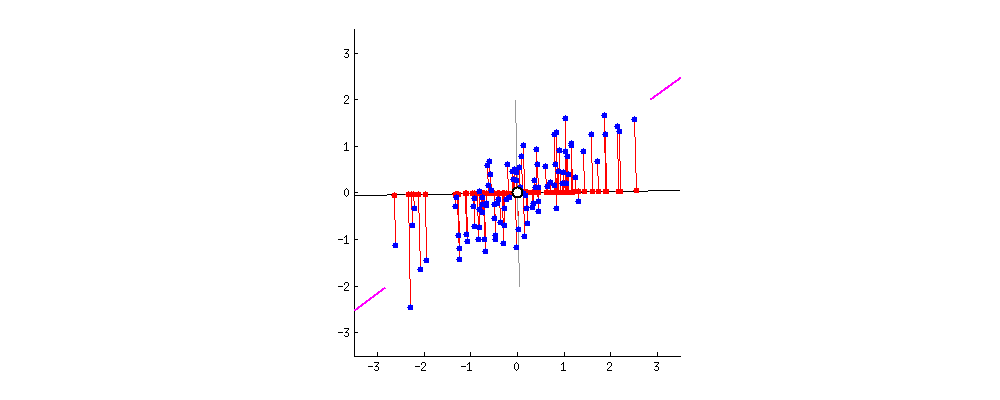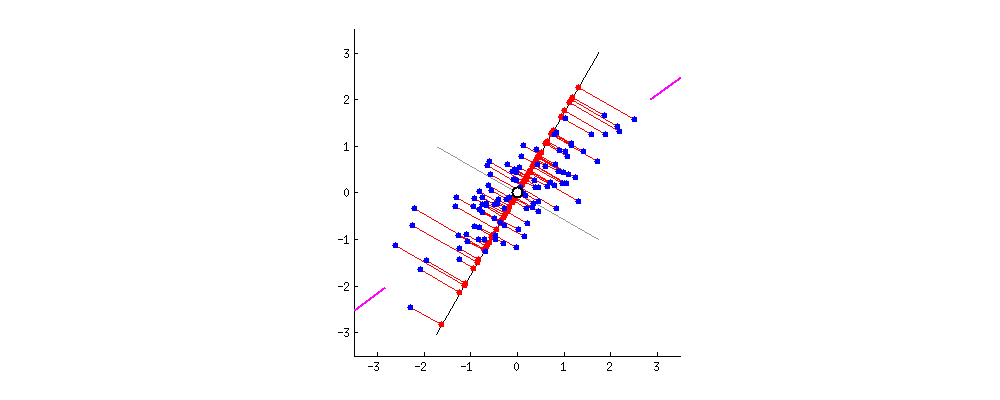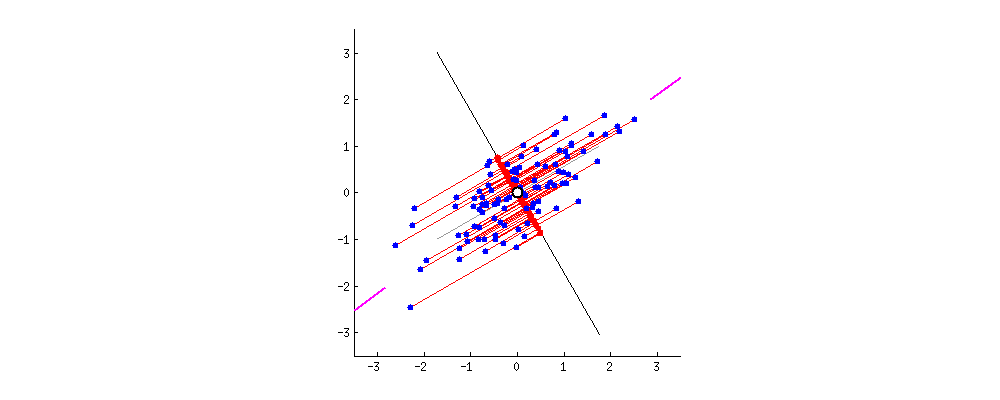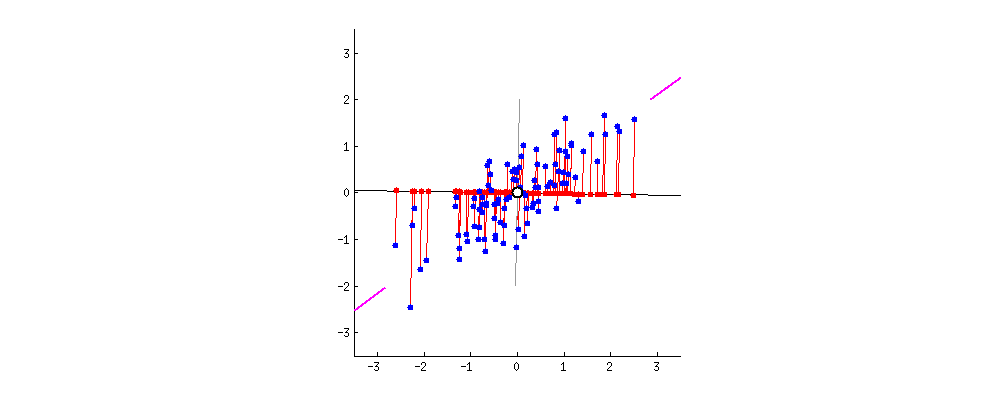
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。具体的,假如我们的数据集是n维的,共有m个数据。我们希望将这m个数据的维度从n维降到n'维,希望这m个n'维的数据集尽可能的代表原始数据集。我们知道数据从n维降到n'维肯定会有损失,但是我们希望损失尽可能的小,转化成数学术语,就是每个行向量的方差尽可能大,行向量间的协方差为0(让属性间尽量不想管,信息尽量转移到某几个单独的属性上,从而实现降维)。
下面以矩阵X为例进行讲解,假设拿到的数据是矩阵X。

它的协方差矩阵则为(假设已实现标准化):
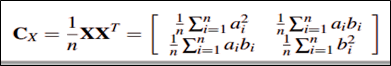
1.1线性变换。现在我们希望降维后的协方差矩阵对角元尽可能大,非对角元尽可能为0,即变成一个对角矩阵。因此我们需要对D做一个线性变换,使得做线性变换后的矩阵的协方差矩阵变成对角矩阵(相当于变化新的坐标)。具体的线性变化过程如下图:
- 若A为实对称矩阵,则A的对应于不同特征值的特征向量也是正交的。
- 实对称矩阵一定正交相似与对角矩阵。

1.2降维。Cy变成对角矩阵后,此时需要将对角元上的特征值进行排序,此时可以把特征值小的那部分对应的信息丢掉,以达到降维的目的。特征值此时代表的就是信息量的大小。具体如下图中的例子:

二、SVD
singular value decomposition
奇异值分解
1、SVD的原理
SVD也是对矩阵进行分解,但是和特征分解不同,SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵,那么我们定义矩阵A的SVD为:

SVD的降维:

为奇异值,且
。
3、SVD与特征分解的关系
奇异值就是 非零的特征值开根号。在PCA应用中,协方差矩阵是正定矩阵,而正定矩阵的奇异分解实质等价于特征分解。

三、PCA与SVD应用的区别
分解:本文中介绍PCA时,为了PCA的通用性,举例时先求A的协方差矩阵,再对A的协方差矩阵进行特征分解,因为PCA的特征分解实际上只能作用于方阵。而SVD使用的奇异值分解则没有这种限制。
降维:SVD通过低秩逼近达到降维的目的。注意到PCA也能达到降秩的目的,但是PCA需要进行零均值化,且丢失了矩阵的稀疏性。
数值稳定性:通过SVD可以得到PCA相同的结果,但是SVD通常比直接使用PCA更稳定。因为PCA需要计算的值,对于某些矩阵,求协方差时很可能会丢失一些精度。





















 2265
2265











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








