迪菲－赫尔曼密钥交换_w. diffie, m. e. hellman, "new directions in crypt-CSDN博客

原文地址：https://zh.wikipedia.org/wiki/%E8%BF%AA%E8%8F%B2%EF%BC%8D%E8%B5%AB%E5%B0%94%E6%9B%BC%E5%AF%86%E9%92%A5%E4%BA%A4%E6%8D%A2

迪菲－赫尔曼密钥交换

维基百科，自由的百科全书

跳转至：导航、搜索

本条目没有列出任何参考或来源。（2012年12月5日）
维基百科所有的内容都应该可供查证。
请协助添加来自可靠来源的引用以改善这篇条目。无法查证的内容可能被提出异议而移除。

迪菲－赫尔曼密钥交换（Diffie–Hellman key exchange，简称“D–H”）是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。

迪菲－赫尔曼密钥交换的同义词包括:

迪菲－赫尔曼密钥协商
迪菲－赫尔曼密钥创建
指数密钥交换
迪菲－赫尔曼协议

这个方案首先由Whitfield Diffie和Martin Hellman于1976发布。后来发现这个方案已经在之前几年由英国信号情报部门发明（发明者为Malcolm J. Williamson），但是当时这被列为是机密。2002年，赫尔曼建议将该算法改名为Diffie–Hellman–Merkle密钥交换以表明Ralph Merkle对于公钥加密算法的贡献(Hellman, 2002)。

虽然迪菲－赫尔曼密钥交换本身是一个匿名 (无认证)的密钥交换协议，它却是很多认证协议的基础，并且被用来提供传输层安全协议的短暂模式中的完备的前向安全性。

该协议的历史

迪菲－赫尔曼密钥交换是1976年在Whitfield Diffie和Martin Hellman的合作下发明的。它是第一个实用的在非保护信道中创建共享密钥方法。它受到了Ralph Merkle的关于公钥分配的工作的影响。John Gill提出了离散对数问题的应用。该方案首先被英国 GCHQ的Malcolm Williamson在稍早的几年前发明，但是GCHQ直到1997年才决定将其公开，这时在学术界已经没有了研究这个算法的热潮了。

这个方法被发明后不久出现了RSA，另一个进行公钥交换的算法。它使用了非对称加密算法。

2002年，Martin Hellman写到:

这个系统...从此被称为迪菲－赫尔曼密钥交换。虽然这个系统首先是在我和迪菲的一篇论文中描述的，但是这却是一个公钥交换系统，是Merkle提出的概念，因此如果加上他的名字，这个系统实际上应该称为'Diffie–Hellman–Merkle密钥交换'。我希望这个小小的讲坛可以帮助我们认识到Merkle对公钥密码学的同等重要的贡献。

The system...has since become known as Diffie–Hellman key exchange. While that system was first described in a paper by Diffie and me, it is a public key distribution system, a concept developed by Merkle, and hence should be called 'Diffie–Hellman–Merkle key exchange' if names are to be associated with it. I hope this small pulpit might help in that endeavor to recognize Merkle's equal contribution to the invention of public key cryptography. [1]

美国专利 4,200,770, 现在已经过期。它描述了这个算法，并且表明了Hellman、Diffie和Merkle是算法的发明者.

描述

迪菲－赫尔曼通过公共信道交换一个信息，就可以创建一个可以用于在公共信道上安全通信的共享秘密（shared secret）。

以下解释它的过程（包括算法的数学部分）：

Diffie–Hellman 密钥交换

最简单，最早提出的这个协议使用一个素数p的整数模n乘法群以及其原根g。下面展示这个算法，绿色表示非秘密信息, and 红色粗体表示秘密信息：

爱丽丝
秘密	非秘密	计算
	p, g
a
		g^a mod p
	…
	(g^b mod p)^a mod p

$\rightarrow$

$\leftarrow$

鲍伯
计算	非秘密	秘密
	p, g
		b
	…
g^b mod p
	(g^a mod p)^b mod p

爱丽丝与鲍伯协定使用 p=23以及base g=5.
爱丽丝选择一个秘密整数a=6, 计算A = g^a mod p并发送给鲍伯。
- A = 5⁶ mod 23 = 8.
鲍伯选择一个秘密整数b=15, 计算B = g^b mod p并发送给爱丽丝。
- B = 5¹⁵ mod 23 = 19.
爱丽丝计算s = B ^a mod p
- 19⁶ mod 23 = 2.
鲍伯计算s = A ^b mod p
- 8¹⁵ mod 23 = 2.

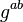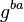爱丽丝和鲍伯最终都得到了同样的值，因为在模p下 $g^{ab}$ 和 $g^{ba}$ 相等。注意a, b 和 g^ab = g^ba mod p 是秘密的。其他所有的值 – p, g, g^a mod p, 以及 g^b mod p – 都可以在公共信道上传递。一旦爱丽丝和鲍伯得出了公共秘密，他们就可以把它用作对称密钥，以进行双方的加密通讯，因为这个密钥只有他们才能得到。当然，为了使这个例子变得安全，必须使用非常大的a, b 以及 p，否则可以实验所有 $g^{ab} \bmod{23}$ 的可能取值(总共有最多22个这样的值, 就算a和b很大也无济于事)。如果 p 是一个至少 300 位的质数，并且a和b至少有100位长，那么即使使用全人类所有的计算资源和当今最好的算法也不可能从g, p和g^a mod p 中计算出 a。这个问题就是著名的离散对数问题。注意g则不需要很大, 并且在一般的实践中通常是2或者5。

以下是一个更为一般的描述:

爱丽丝和鲍伯写上一个有限循环群 G 和它的一个生成元生成元 g。（这通常在协议开始很久以前就已经规定好； g是公开的，并可以被所有的攻击者看到。）
爱丽丝选择一个随机自然数 a 并且将 $g^{a} \bmod{p}$ 发送给鲍伯。
鲍伯选择一个随机自然数 b 并且将 $g^{b} \bmod{p}$ 发送给爱丽丝。
爱丽丝计算 $\left ( g^{b} \right )^{a} \bmod{p}$ 。
鲍伯计算 $\left ( g^{a} \right )^{b} \bmod{p}$ 。

爱丽丝和鲍伯就同时协商出群元素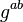 $g^{ab}$ ，它可以被用作共享秘密。 $\left ( g^{b} \right )^{a}$ 和 $\left ( g^{a} \right )^{b}$ 因为群是乘法交换的。 (见幂.)

图示

下面的图示可以方便你理解每个信息都只有谁知道。（伊芙是一个窃听者—她可以看到爱丽丝和鲍伯的通讯内容，但是无法改变它们）

Let s = 共享密钥。 s = 2

Let a = 爱丽丝的私钥。如 a = 6
Let A = 爱丽丝的公钥。如 A = g^a mod p = 8
Let b = 鲍伯的私钥。如 b = 15
Let B = 鲍伯的公钥。如 B = g^b mod p = 19
Let g = 公共原根。如 g=5

Let p = 公共质数. 如 p = 23

爱丽丝
知道	不知道
p = 23
base g = 5
a = 6
	b = 15
A = 5⁶ mod 23 = 8
B = 5^b mod 23 = 19
s = 19⁶ mod 23 = 2
s = 8^b mod 23 = 2
s = 19⁶ mod 23 = 8^b mod 23
s = 2

鲍伯
知道	不知道
p = 23
base g = 5
	a = 6
b = 15
B = 5¹⁵ mod 23 = 19
A = 5^a mod 23 = 8
s = 8¹⁵ mod 23 = 2
s = 19^a mod 23 = 2
s = 8¹⁵ mod 23 = 19^a mod 23
s = 2

伊芙
知道	不知道
p = 23
base g = 5
	a = 6
	b = 15
A = 5^a mod 23 = 8
B = 5^b mod 23 = 19
s = 19^a mod 23
s = 8^b mod 23
s = 19^a mod 23 = 8^b mod 23
	s = 2

注意：对爱丽丝来说解开鲍伯的私钥或鲍伯要解开爱丽丝的私钥应该都很困难。如果对爱丽丝来说解开鲍伯的私钥不难的话（反之亦然），伊芙可以轻易地替换掉她自己的私钥/公钥对，把鲍伯的公钥插到她自己的私钥，产生出一个假的共享密钥，并解开鲍伯的私钥（然后用这个解开共享私钥。伊芙可以试着选择一个能让她轻松解开鲍伯的私钥的公钥/私钥对）。

安全性

在选择了合适的G和g时，这个协议被认为是窃听安全的。偷听者("Eve")可能必须通过求解迪菲－赫尔曼问题来得到g^ab。在当前，这被认为是一个困难问题。如果出现了一个高效的解决离散对数问题的算法，那么可以用它来简化a或者b的计算，那么也就可以用来解决迪菲－赫尔曼问题，使得包括本系统在内的很多公钥密码学系统变得不安全。

G的阶应当是一个素数，或者它有一个足够大的素因子以防止使用Pohlig–Hellman算法来得到a或者b。由于这个原因，一个索菲热尔曼素数 q可以用来计算素数p=2q+1，这样的p称为安全素数，因为使用它之后G的阶只能被2和q整除。g有时被选择成G的q阶子群的生成元，而不是G本身的生成元，这样g^a的勒让德符号将不会显示出a的低位。

如果Alice和Bob使用的随机数生成器不能做到完全随机并且从某种程度上讲是可预测的，那么Eve的工作将简单的多。

秘密的整数a和b在会话结束后会被丢弃。因此，迪菲－赫尔曼密钥交换本身能够天然地达到完备的前向安全性，因为私钥不会存在一个过长的时间而增加泄密的危险。

身份验证

在最初的描述中，迪菲－赫尔曼密钥交换本身并没有提供通讯双方的身份验证服务，因此它很容易受到中间人攻击。一个中间人在信道的中央进行两次迪菲－赫尔曼密钥交换，一次和Alice另一次和Bob，就能够成功的向Alice假装自己是Bob，反之亦然。而攻击者可以解密（读取和存储）任何一个人的信息并重新加密信息，然后传递给另一个人。因此通常都需要一个能够验证通讯双方身份的机制来防止这类攻击。

有很多种安全身份验证解决方案使用到了迪菲－赫尔曼密钥交换。当Alice和Bob共有一个公钥基础设施时，他们可以将他们的返回密钥进行签名，也可以像MQV那样签名g^a和g^b；STS以及IPsec协议的IKE组件已经成为了Internet协议的一部分；当Alice和Bob共享一个口令时，他们还可以从迪菲－赫尔曼算法使用口令认证密钥协商，类似于ITU-T的建议X.1035。这已经被用作了G.hn的家庭网络标准。

参见

引用

Dieter Gollmann (2006). Computer Security Second Edition West Sussex, England: John Wiley & Sons, Ltd.
Non-Secret Encryption Using a Finite Field MJ Williamson, January 21, 1974.
Thoughts on Cheaper Non-Secret Encryption MJ Williamson, August 10, 1976.
New Directions in Cryptography W. Diffie and M. E. Hellman, IEEE Transactions on Information Theory, vol. IT-22, Nov. 1976, pp: 644–654.
Cryptographic apparatus and method Martin E. Hellman, Bailey W. Diffie, and Ralph C. Merkle, U.S. Patent #4,200,770, 29 April 1980
The History of Non-Secret Encryption JH Ellis 1987 (28K PDF file) (HTML version)
The First Ten Years of Public-Key Cryptography Whitfield Diffie, Proceedings of the IEEE, vol. 76, no. 5, May 1988, pp: 560–577 (1.9MB PDF file)
Menezes, Alfred; van Oorschot, Paul; Vanstone, Scott (1997). Handbook of Applied Cryptography Boca Raton, Florida: CRC Press. ISBN 0-8493-8523-7. (Available online)
Singh, Simon (1999) The Code Book: the evolution of secrecy from Mary Queen of Scots to quantum cryptography New York: Doubleday ISBN 0-385-49531-5
An Overview of Public Key Cryptography Martin E. Hellman, IEEE Communications Magazine, May 2002, pp:42–49. (123kB PDF file)